Файл: Нод и нок многочленов.docx

МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ

УНИВЕРСИТЕТ»

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
КУРСОВАЯ РАБОТА
БАКАЛАВРА

по направлению подготовки 44.03.05 «Педагогическое образование»

(с двумя профилями подготовки)

профили "Математика", "Физика"

Дисциплина «Алгебра»

На тему: «НОД и НОК многочленов»

Выполнила: студентка 3 курса

физико-математического факультета

Беляева Яна Алексеевна



Научный руководитель:

канд. физ.-мат. наук,

доцент кафедры высшей математики

Петросян Гарик Гагикович

Воронеж – 2023

Содержание

Введение

Ежедневно каждый человек решает множество различных задач. Для успешного решения часто приходиться пользоваться определёнными математическими правилами. Мы не задумываемся о ценности применения различных методов и определённых знаниях. Данная работа расширяет знания о вычислениях НОД и НОК в многочленах. Знакомство с ними не только дополняет и углубляет математические знания, но и развивает интерес к предмету, любознательность и логическое мышление. Данная работа рассчитана на учеников, желающих повысить уровень математической подготовки, увидеть красоту математических преобразований и красоту алгоритма Евклида.

В данной курсовой работе мы будем иметь дело с: многочленами, наибольшим общим делителем, наименьшим общим кратным и алгоритмом Евклида.

---

Актуальность исследования. В школьном курсе математики, когда обучающиеся только начинают знакомиться с записью математических выражений и предложений при помощи букв, а также выполнять арифметические действия над ними, искать неизвестные компоненты по известным.

Далее при переходе на изучение уже курса алгебры ключевым становится понятие «многочлен», обучающиеся учатся овладевать навыками преобразований целых и дробных выражений, содержащих цифры и буквы, формируют представление об способах извлечения корня, а также знакомятся с понятием «уравнение», знакомятся с формулами сокращенного умножения. И не имея систематизированных знаний о многочленах, ребенку достаточно сложно даются математические операции, особенно в случае, когда он не владеет понятийным аппаратом.

В последние несколько десятилетий большое внимание уделяется образовательной функции математики. Методисты и педагоги придерживаются нескольких разных по сути подходов к структуре изучаемых курсов, существующие образовательные программы и учебно-методические комплексы разнообразны, так что каждому педагогу при написании программы по математике необходимо производить анализ методических особенностей изучения для каждой конкретной темы.

И особого внимания требует методика обучения теме «НОД и НОК многочленов», которая является основополагающей при изучении линии тождественных преобразований на протяжении всего курса математики в основной школе. Основные понятия, которые рассматриваются в данной теме, находят свое отражение и в контрольно-измерительных материалах ОГЭ по математике.

Целью данной курсовой работы является исследование теоретического материала по теме «НОД и НОК многочленов», алгоритма Евклида, а также ознакомление с различными алгоритмами вычисления НОД и НОК многочленов.

Для выполнения курсовой работы я поставила следующие задачи:

1. 
   Расширить знания о многочленах;
   
2. 
   Изучить теорию по теме «НОД и НОК в многочленах»;
   
3. 
   Познакомиться с Алгоритмом Евклида.
   

---

Методы исследования:

• 
  Изучение специальной литературы по данному вопросу: энциклопедии, справочники, учебные пособия и др.;
  
• 
  Сравнение и анализ;
  
• 
  Обработка и систематизация полученных данных.
  

---

Глава 1. Общие сведения о многочленах

1. 
   Основные определения и простейшие свойства
   

Пусть 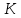— произвольное кольцо. Многочленом, или полиномом, от переменной x называется выражение вида

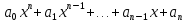(1.1)

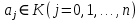где , а 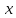— символ, называемый независимой переменной. Многочлены, как правило, мы будем обозначать латинскими буквами, рядом с которыми иногда в скобках ставить имя независимой переменной. Например, многочлен (1.1) обозначим 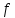, или, что эквивалентно, 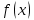, тогда можно записать:

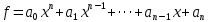(1.2)

Величины 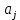называются коэффициентами многочлена, а выражения 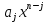— членами (или мономами) многочлена 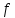, при этом 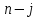называется степенью монома. Если 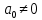, то 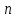называется степенью многочлена, а 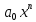— его старшим членом. Степень многочлена обозначается 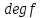. Многочлен 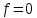называется нулевым; его степень не определена. Многочлены 1-й, 2-й и 3-й степени называются линейными, квадратными и кубическими соответственно. Многочлены нулевой степени вместе с нулевым многочленом называют константами. В записи (1.2) члены с нулевым коэффициентом обычно опускают. Также используют другие обычные соглашения при работе с алгебраическими выражениями, например, вместо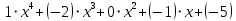

---

пишут 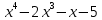. Помимо записи (5.2), в которой члены записаны в порядке убывания степеней, часто используется запись с упорядочением членов по возрастанию степеней и др. записи. Два многочлена (1.2) и

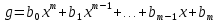(1.3)

равны, есл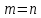и и 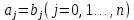. Таким образом, мы принимаем алгебраическую точку зрения на многочлены. Возможна также другая — «функциональная» — точка зрения, по которой многочлены рассматриваются как функции 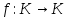. Над конечными полями эти точки зрения не эквивалентны. Например, неравные многочлены 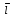и 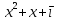над полем 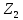задают одну и ту же функцию (тождественную ).

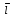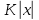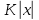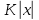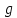Множество всех многочленов с коэффициентами из кольца обозначим . Это множество называют еще множеством многочленов над кольцом . Многочлены из можно складывать и умножать. При этом снова получается многочлен из . Сложение и умножение многочленов выполняется по обычным правилам преобразования алгебраических выражений. Для определения суммы многочленов и , определенных согласно (1.2) и (1.3), предположим, что 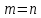(чтобы это условие выполнялось припишем, если необходимо,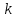 или

---