Файл: Опорн консп_СТАТ.doc

Середні величини можуть бути абсолютними або відносними залежно від вихідної бази для розрахунку. Найпоширенішою в економічних розрахунках є середня арифметична (проста або зважена), її обчислюють додаванням окремих величин і діленням суми на кількість величин:

де х – варіанти;

n– кількість показників (варіантів).

Типова задача 3

Дані про місячну заробітну плату п’яти робітників в цеху, грн.:150, 160, 180, 190, 210. Визначити середню місячну заробітну одного робітника.

Розв’язання:

Середню арифметичну зважену застосовують тоді, коли різні варіанти ознаки в сукупності, що досліджується, повторюються неоднаково. Число, що показує, скільки разів повторюється даний варіант, називається частотою або вагою, і позначається через f:

Типова задача 4

Дані про капітальні витрати на підприємствах:

Група підприємств за розміром капітальних витрат, тис.грн.	Кількість підприємств
8-10	6
10-12	8
12-14	15
14-16	15
16-18	10
18-20	6
Разом	60

Визначити середній розмір капітальних витрат на одне підприємство. Щоб визначити середню арифметичну інтервального ряду, потрібно для кожного інтервалу знайти його середину і після цього робити обчислення за наведеною вище формулою:

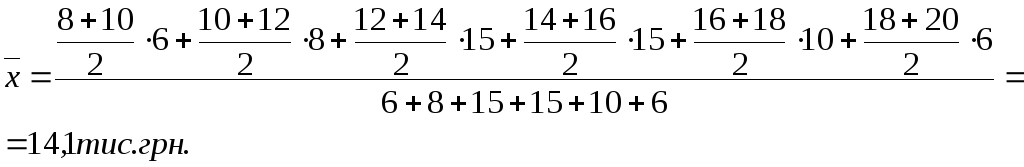
Не завжди за формулою середньої арифметичної можна отримати правильну середню величину. Наприклад, коли є дані про загальний обсяг й індивідуальні значення ознаки, то відомостей про кількість одиниць явища, що досліджується, немає.

Середня гармонічна – це обернена величина до середньої арифметичної, обчисленої з обернених величин осередаюваних варіюючих ознак.

Середня гармонічна проста:

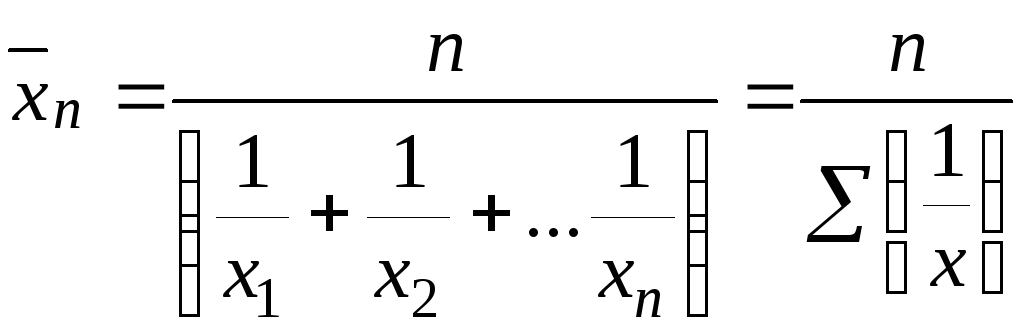
Середня гармонічна зважена:

;

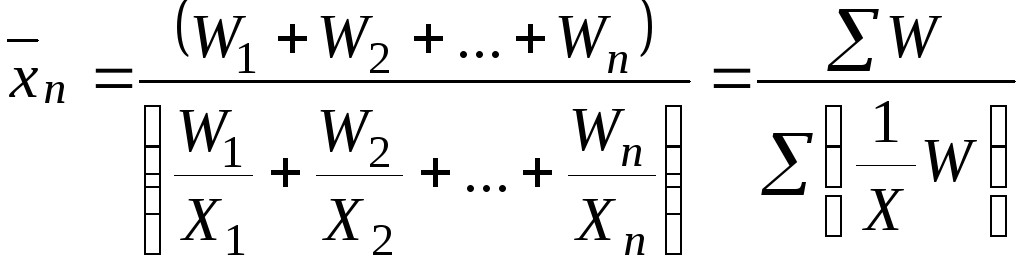
де W – вага

Типова задача 5

За даними про обсяг реалізації побутових послуг 1 середній виробіток одного робітника по цехах визначити середній виробіток кожного робітника по підприємству.

Номер цеха	Обсяг реалізації побутових і послуг, тис. грн.	Місячний виробіток одного робітника, тис. грн.
1	57	1,9
2	46	2,0
3	65	2,5
4	52	2,6

Розв’язання:

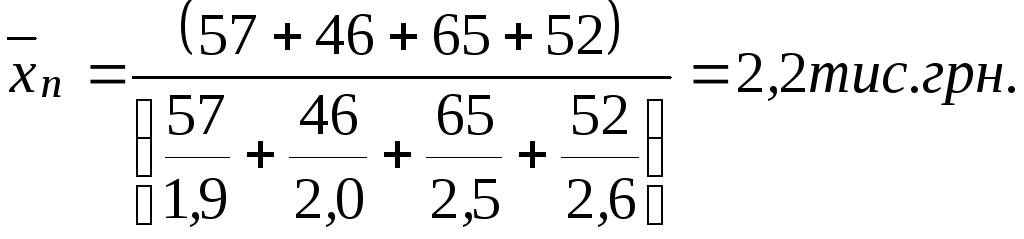
Для характеристики величин варіюючої ознаки використовують моду й медіану.

Модою називається величина, яка в ряді повторюється найчастіше. Для дискретного ряду розподілу модою є значення варіанта, що має найбільшу частоту.

Тарифний розряд 1,2,3,4,5,6.

Кількість робітників – 7, 10, 12, 8, 3.

Mo = 4. Це означає, що найбільше робітників ІV розряду.

де М₀ – мода;

Х₀ – нижня межа модального інтервалу;

i – величина модального інтервалу;

f₁, f₂_,f₃– частота інтервалу відповідно перед модальним, модального і після нього.

Типова задача 6

Дані про розподіл 200 робітників заводу за денним виробітком.

Група робітників з денним виробітком, шт.	Кількість робітників, чол.
7-9	12
9-11	23
11-13	85
13-15	55
15-17	25
Разом	200

Визначити моду.

Медіана – це величина ознаки, що займає середнє положення у варіаційному ряді, в якому варіанти розміщені в зростаючому або спадаючому порядку, її називають середнім варіантом. Якщо поставити в ряд за зростом 15 студентів, то зріст 8-го студента від початку або кінця буде медіаною. Якщо в ряду 16 студентів, то медіаною буде середнє значення зросту 8-го і 9-го студентів.

Медіана для інтервального варіаційного ряду

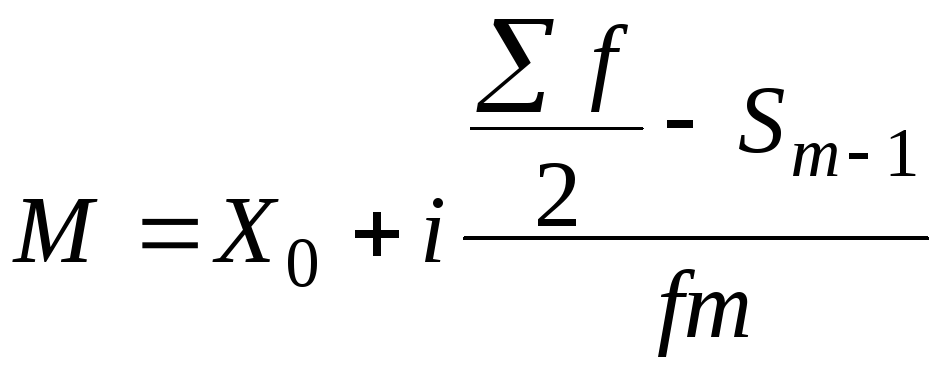
де Х₀– нижня межа медіанного інтервалу;

і – величина медіанного інтервалу;

∑f – сума частот;

S_m_-1– сума нагромаджених частот перед медіанним інтервалом;

F_m– частота медіанного інтервалу.

Щоб визначити медіану інтервального варіаційного ряду треба знайти інтервал, що містить медіану, за допомогою нагромаджених частот.

Медіанному інтервалу відповідає перша з нагромаджених частот яка перевищує половину всього обсягу сукупності півсума частот .дорівнює 100/. Отже, медіана міститься в інтервалі 11…1З шт. Підставивши значення в наведену вище формулу знайдемо:

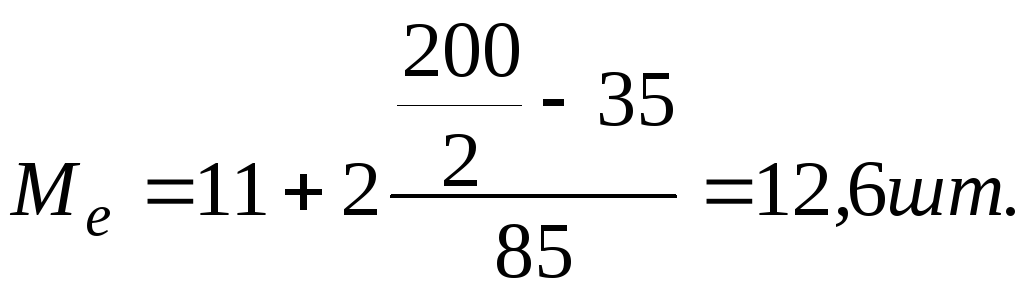
Середня величина відображає лише загальне, що властиве сукупності явищ, і не показує, як розміщуються біля неї варіанти усередненої ознаки. Тому цю величину треба доповнювати показниками які характеризують коливання (варіації) ознак у сукупності.

Для визначення розміру варіації в статистиці використовують різні показники: розмах варіації, середнє лінійне відхилення, середній квадрат відхилення (дисперсія), середнє квадратичне відхилення, коефіцієнт варіації.

Розмах варіації становить різницю між найбільшим і найменшим значеннями ознаки.

Середнє лінійне відхилення являє собою середню арифметичну з абсолютних значень відхилень окремих варіант від їх середньої арифметичної величини.

Середнє лінійне відхилення – величина іменована і визначається в тих самих одиницях виміру, що й варіанти. Його обчислюють за такими формулами:

- просте середнє лінійне відхилення;

- зважене середнє лінійне відхилення;

Середній квадрат відхилення, або дисперсія, становить середню арифметичну з квадратів відхилень окремих варіантів від їх середньої. Належно від вихідних даних дисперсію обчислюють за простою або зваженою середнього арифметичного.

- дисперсія незважена (проста);

- дисперсія зважена.

Дисперсія альтернативної ознаки:

де р – частка одиниць сукупності, що має дану ознаку;

q – частка одиниць сукупності, що даної ознаки не має.

Корінь квадратний з дисперсії називається середнім квадратичним відхиленням. Середнє квадратичне відхилення визначають за такими формулами:

- середнє квадратичне відхилення незважене (просте)

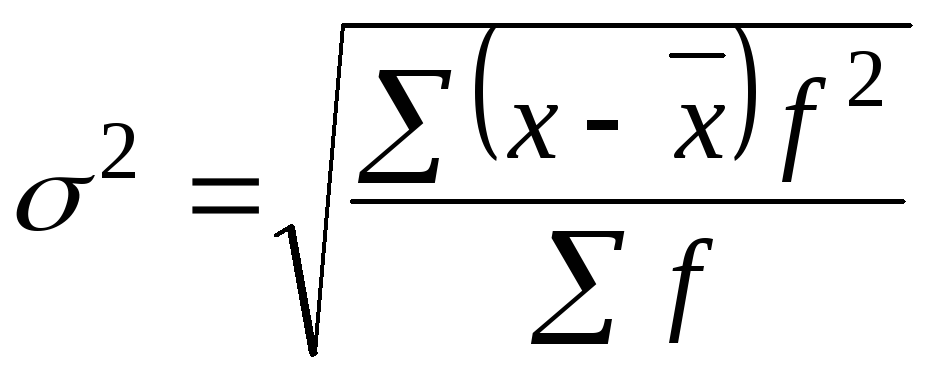- середнє квадратичне відхилення зважене.

Щоб порівняти середні квадратичні відхилення різних варіаційних рядів, треба перейти від абсолютних показників коливання до відносних.

Відносною характеристикою коливання (варіації) є процентне відношення середнього квадратичного відхилення до середньої арифметичної. Це відношення називається коефіцієнтом варіації. Коефіцієнт варіації може бути обчислено і за лінійним квадратичним відхиленням.

Типова задача 7

Дані про розподіл підприємств однієї з галузей промисловості за величиною основних фондів. Визначити показники варіації.

Група підприємств з величиною основних фондів, млн. грн.	Кількість підприємств
1-3	15
3-5	30
5-7	20
7-9	15
9-11	15
11 і більше	5
Разом	100

Розв’язання:

Для визначення показників варіації складемо таку таблицю.

Група підп-риємств з ве-личиною ос-новних фон-дів, млн. грн.	Кількість підприємств, f	Сере-дина інтер-вала, Х
1-3	15	2	30	-4	-60	16	240	60
3-5	30	4	120	-2	-60	4	120	480
5-7	20	6	120	0	0	0	0	720
7-9	15	8	120	2	30	4	60	960
9-11	15	10	150	4	60	16	2401	1500
11 і більше	5	12	60	6	30	36	180	720
Разом	100	-	600	-	0	-	840	4440