Файл: Опорн консп_СТАТ.doc

Середня арифметична:

Розмах варіації: R=12-2=10 млн.грн.

Середнє лінійне відхилення:

Середній квадрат відхилення (дисперсия):

Середнє квадратичне відхилення:

Коефіцієнт варіації: = 40%

---

Тема статистичні методи вимірювання взаємозв'язків

Обговорення питань:

1. Поняття про кореляційний аналіз. Парна і множинна кореляція.

2. Кореляційне поле і кореляційні таблиці. Встановлення форм зв'язку. Побудова рівнянь зв'язку. Визначення параметрів рівняння зв’язку. Криволінійна регресія.

3. Щільність зв’язку між ознаками. Коефіцієнти детермінації і кореляції. Індекс кореляції.

4. Визначення суттєвості коефіцієнту регресії і кореляції, одержаних за вибірковими даними. Визначення інтервалів надійності показників зв'язку.



Явища у суспільстві пов'язані між собою. Для вивчення зв’язків статистика використовує певні методи. До таких методів відносяться: графічний, групувань, кореляційний, регресивний, дисперсійний.

Кореляційний зв'язок на відміну від функціонального виявляється не в кожному окремому випадку, а в середньому, в цілому для багатьох випадків.

За формулою зв'язку кореляційні залежності бувають прямолінійними і криволінійними. При прямолінійній кореляційній залежності рівним змінам середніх значень факторної ознаки відповідають приблизно рівні зміни середніх значень результативної ознаки. При криволінійній кореляційній залежності рівним змінам середніх значень факторної ознаки відповідають нерівні зміни середніх значень результативної ознаки.

В економічних дослідженнях часто доводиться мати справу з прямолінійною формулою зв'язку, яка визначається рівнянням прямої.

,

де -ординати шуканої прямої;

а і b – параметри прямої.

П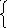араметрирівняння прямої лінії визначаються способом найменших квадратів. Суть його полягає у складанні і розв’язанні системи двох рівнянь з двома невідомими.

де n – кількість членів у кожному з двох рядів, що порівнюються.

---

Розв’язавши цю систему, дістаємо:

Типова задача 8

Дані на підприємствах галузі.

Номер підприємства	Виробництво продукції на одного працюючого, млн.грн. Y	Енергоозброєність праці на одного працюючого, кВг.год X	Х2	ХУ
1	5,0	5	25	25,0
2	6,5	7	49	45,5
3	6,2	6	36	37,2
4	7,1	8	64	56,8
5	6,8	4	16	27,2
6	4,5	5	25	22,5
7	7,2	7	49	50,4
8	8,3	8	64	66,4
9	6,4	5	25	32,0
10	3,8	4	16	15,2
n = 10	61,8	59	369	378,2

Підставивши дані у наведені формули, матимемо:

---

Отже рівняння зв'язку між виробництвом продукції на одного працюючого та енергоозброєністю матиме такий вигляд:

Для аналітичного вираження криволінійної залежності використовують гіперболічне і параболічне кореляційні рівняння.

Рівняння гіперболи має вигляд:

Щоб визначити параметри a i b цього рівняння способом найменших квадратів, складають і розв'язують систему рівнянь з двома невідомими.

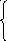
Типова задача 9

Дані на підприємствах галузі:

Номер підприємства	Собівартість одиниці продукції, грн. Y	Вироблено продукції, тис.шт. X	1/x	(1/x)2	(1/x)y
1	2,3	45	0,022	0,000484	0,0506	2,6
2	2,5	48	0,021	0,000441	0,0525	2,8
3	2,0	40	0,025	0,000625	0,0500	2,0
4	2,8	51	0,021	0,000441	0,0588	3,1
5	3,0	50	0,020	0,000400	0,0600	3,0
6	2,4	38	0,026	0,000676	0,0624	1,7
7	3,2	55	0,018	0,000324	0,0576	3,4
8	4,0	60	0,017	0,000289	0,0680	3,7
9	2,1	41	0,024	0,000576	0,0504	2,1
10	3,5	56	0,018	0,000324	0,0630	3,4
Разом	27,8	484	0,212	0,004580	0,5733	27,8

---

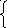
Розв’язавши цю систему, дістаємо:

a = 7,02;

b= -200.

Отже рівняння зв’язку між собівартістю одиниці продукції та виробництвом продукції матиме такий вигляд:

Рівняння параболи другого порядку можна записати так:

Параметри a, b, c обчислюють розв‘язанням системи нормальних рівнянь:

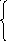
Для того щоб встановити ступінь кореляційної залежності міх ознаками, користуються показниками щільності зв'язку: коефіцієнтом кореляції, кореляційним відношенням.

При лінійній кореляційній залежності щільність зв'язку визначають за формулою коефіцієнта кореляції:

де -лінійний коефіцієнт кореляції;

- коефіцієнт регресії в рівнянні зв’язку;

- середнє квадратичне відхилення ознак х і у.

Лінійний коефіцієнт кореляції можна визначати також за іншими формулами:

або

На підставі даних задачі 8 обчислюємо лінійний коефіцієнт кореляції. Для цього треба визначити значення таких величин: x, y, xy, ,. Визначаємо:

---