Файл: Опорн консп_СТАТ.doc

- середнє значення факторної ознаки:

- середнє значення результативної ознаки:

- середнє значення добутку факторної і результативної ознаки:

- середнє квадратичне відхилення факторної ознаки:

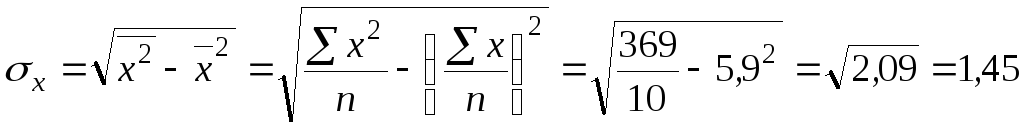
- середнє квадратичне відхилення результативної ознаки:

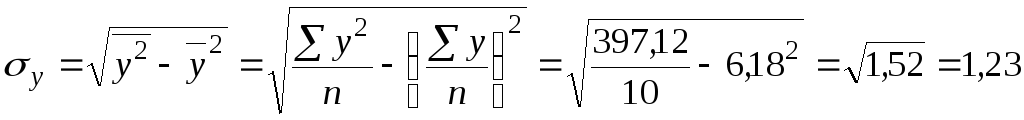
- лінійний коефіцієнт кореляції:

Отже, зв'язок виробництва продукції на одного працюючого з енергоозброєністю праці - щільний.

---

Тема аналіз інтенсивності динаміки. Аналіз тенденцій розвитку та коливань

Обговорення питань:

1. Статистичні ряди динаміки і основні правила їх побудови

2. Види рядів динаміки. Показники рядів динаміки

3. Прийоми аналізу рядів динаміки

4. Вивчення сезонних коливань



Усі явища в природі й суспільстві розвиваються у просторі й часі. Процеси розвитку суспільних явищ у часі називають динамікою, a статистичні показники, які характеризують зміну суспільних явищ, - рядами динаміки.

Ряди динаміки поділяють на ряди динаміки абсолютних, відносних і середніх величин.

Залежно від характеру рівнів динамічного ряду розрізняють два види рядів динаміки: інтервальні й моментні.

Інтервальний – це ряд динаміки, рівні якого характеризують розміри суспільних явищ за певні періоди.

Це, наприклад, дані про валовий збір зерна в Україні за 2004-2008 рр.; тис.т.

Валовий збір зерна в Україні

2004	2005	2006	2007	2008
51009	38674	38537	45623	35497

Момент ний – це ряд динаміки рівні якого характеризують стан явища на певний момент часу.

Прикладом такого ряду можуть бути дані про кількість пенсіонерів в Україні (на початок кожного року) ,тис.чол.

Кількість пенсіонерів в Україні

2000	2001	2002	2003	2004
13084	13554	14191	14477	14515

В інтервальних рядах динаміки з різними інтервалами часу середній рівень ряду обчислюють за формулою середньої арифметичної простої:

---

Середній рівень моментного ряду обчислюють за формулою середньої хронологічної:

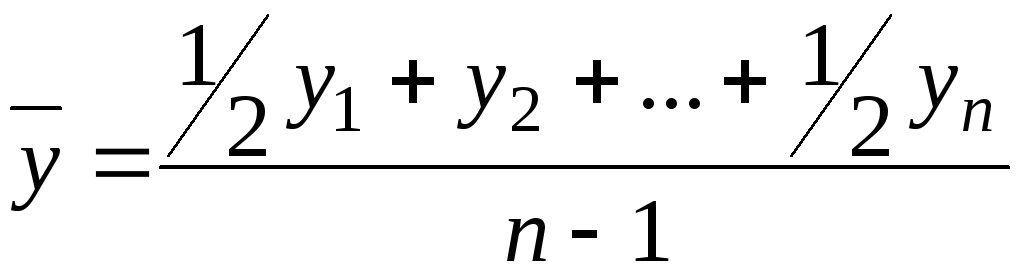
де y₁ ... y_n – рівні ряду;

n – кількість рівнів.

У процесі аналізу динаміки суспільних явищ визначають абсолютний приріст, темпи зростання, приросту, абсолютне значення 1% приросту на основі порівняння рівнів ряду динаміки. За базу порівняння беруть попередній, або початковий рівень динаміки.

Якщо кожний рівень порівнюють з попереднім то такі показники називають ланцюговими. Коли всі рівні порівнюють з тим самим рівнем, що є постійною базою порівняння, то такі показники називають базисними.

Абсолютній приріст показує на скільки одиниць підвищився або зменшився поточний рівень порівняно з базисним, тобто за той чи інший період часу.

де П – абсолютний приріст за t-у одиниць часу;

у_i - порівнюваний рівень;

y_i-t - базисний рівень.

Якщо за базу порівняння взяти попередній рівень, матимемо таку формулу ланцюгових абсолютних приростів:

де y_і-1 - рівень попереднього періоду відносно порівнюваного.

Темп зростання показує, у скільки разів збільшився порівнюваний рівень відносно базисного.

Якщо за базу порівняння взяти попередній рівень, дістаємо ланцюгові темпи зростання.

Між ланцюговими і базисними темпами зростання, вираженими у вигляді коефіцієнтів, є певний взаємозв'язок. Добуток послідовних ланцюгових темпів зростання дорівнює базисному темпу зростання за відповідний період і, навпаки, поділивши наступний базисний темп зростання на попередній, матимемо відповідний ланцюговий темп зростання.

Темп приросту становить відношення абсолютного приросту до базисного рівня

Темп приросту можна визначити також відніманням від темпів зростання величини 100 або 1.

---

Абсолютне значення 1% приросту дорівнює відношенню абсолютного приросту до темпу приросту за той самий період.

де А – абсолютна величина 1% приросту.

Середній темп зростання визначають за формулою середньої геометричної.

Середня геометрична кількох величин дорівнює кореню n-ої степені з їх добутку, показник ступеня якого дорівнює кількості співмножників.

де – середній темп зростання;

T1,Т2... Tn – коефіцієнти зростання, обчислені відносно попередніх рівнів;

n – число коефіцієнтів зростання.

Щоб обчислити середній темп зростання, користуються формулою:

де у_{і ,}у₁ – відповідно кінцевий і базисний рівні ряду;

n – кількість рівнів динамічного ряду.

Типова задача 10

За наведеними даними визначити показники ряду динаміки.

Квартал	Вироблено продукції, тис.шт.
1	3,4
2	4,4
3	5,0
4	6,1

Розв’язання:

1) Абсолютний приріст, тис.шт.:

Ланцюговий	Базисний
4.4 – 3.4 = 1.0	4.4 – 3.4 = 1.0
5.0 – 4. 4 = 0.6	5.0 – 3.4 = 1.6
6.1 – 5.0 = 1.1	6.1 – 3.4 = 2.7

2) Темп зростання, %:

Ланцюговий	Базисний
4.4/3.4*100 = 129,4	4.4 / 3.4*100 = 129,4
5.0 /4.4*100 = 113,6	5.0 /3.4 *100 = 147,1
6.1 / 5.0*100 = 122,0	6.1/ 3.4*100 = 179,4

---

3) Темп приросту, %:

Ланцюговий	Базисний
1,0/3.4*100 = 29,4 або 129,4-100=29,4	1,0 / 3.4*100 = 29,4
0,6 /4.4*100 = 13,6	1,6 /3.4 *100 = 47,1
1,1 / 5.0*100 = 22,0	2,7/ 3.4*100 = 79,4

4) Абсолютне значення 1% приросту:

До методів аналізу рядів динаміки відносять інтерполяцію, екстраполяцію, вимірювання сезонних коливань.

При побудові й вивченні рядів динаміки важливо переконатись у зіставленні рівнів рядів.

Подолання випадків відсутності зіставлення розглянемо на прикладах.

Типова задача 11

Дані про виробництво молока УКСП району, тис. т.

Рік	1986	1987	1988	1989	1990	1991	1992
У старих межах району	16,5	17,8	18,7	19,6
У нових межах району				21,0	23,4	23,8	25,1

Розв’язання:

Наведені дані не порівнюються. Необхідно їх порівняти або зімкнути ряд динаміки. Для цього за основу перерахунку візьмемо 1989 рік. Визначимо коефіцієнт співвідношення рівнів цього року:

Перерахунок рівнів за 1986-1988 рр.

16,5*1,071 = 17,7

17,8*1,071 = 19,1

18,7*1,071 = 20,0.

---