ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.04.2024
Просмотров: 121
Скачиваний: 0
Тема 2: Начала проекционного черчения п.1 Понятие о разных родах проекций
Проекционное черчение имеет целью указать способы, посредством которых можно изобразить на плоскости любое геометрическое тело таким образом, чтобы по чертежу можно было составить точное представление о величине, форме и взаимном расположении всех частей изображенного тела.
Различают проекции трех родов.
1.Центральная (или перспективная) проекция. Положим, мы желаем изобразить (черт. 1) на плоскости V (обыкновенно она называется картинной плоскостью или экраном) какую-нибудь фигуру, например ∆ ABC (помещенный где-нибудь за экраном), в таком виде, в каком он представляется нашему глазу, если будем смотреть на него из точки О (называемой центром перспективы). Так как каждую видимую точку предмета мы всегда видим по прямой линии, проходящей от глаза через эту точку (такая линия называется лучом зрения), то для получения
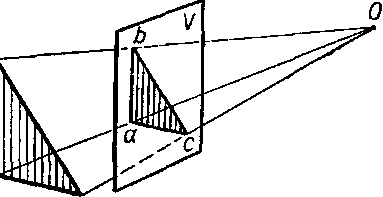
Черт. 1
чертежа на плоскости V надо найти точки, в которых с этой плоскостью пересекаются лучи зрения, идущие к глазу от разных точек предмета.
Фигура abc, полученная таким образом на плоскости V, будет центральной проекцией (перспективой) фигуры ABC.
Примером таких изображений могут служить фотографические снимки.
Косоугольная проекция.
Прямоугольная(ортогональная) проекция. Вообразим, что центр перспективы (и, следовательно, наш глаз, предполагаемый в этом центре) удаляется от предмета на все большее и большее расстояние; тогда лучи зрения, идущие от разных точек фигуры к глазу, делаются все более и более параллельными между собой, и если мы их предположим совершенно параллельными (т. е. допустим, что центр перспективы удален бесконечно далеко от предмета), то мы получим параллельную проекцию (черт. 2), которая бывает или косоугольная, если параллельные лучи зрения наклонны к экрану, или прямоугольная (ортогональная), если эти лучи перпендикулярны к экрану.

Черт. 2
Примером чертежей, представляющих собой косоугольные проекции, служат те стереометрические чертежи, которые мы имеем в этой работе; примером прямоугольных проекций служат планы и фасады зданий, исполненные (конечно, в уменьшенном масштабе) на архитектурных проектах.
Мы рассмотрим только общие свойства параллельных проекций, как ортогональных, так и косоугольных.
П.2 Общие свойства параллельных проекций
Определения. 1. Проекцией данной точки (А, черт. 3) на какую-нибудь плоскость (V) называется та точка (а) этой плоскости, в которой с ней пересекается прямая (AM), проведенная из данной точки параллельно заданному направлению (ху).
Прямая AM называется в таком случае проектирующей прямой, а плоскость V — плоскостью проекций. Если проектирующая прямая перпендикулярна к плоскости проекций, то проекция называется прямоугольной или ортогональной, в противном случае — косоугольной.
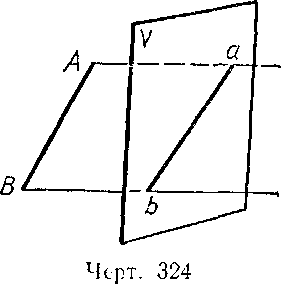
Черт. 3
2. Проекцией какой-нибудь фигуры на данную плоскость называется геометрическое место проекций всех точек этой фигуры на эту плоскость.
Свойства проекции прямых линий.
|
Свойства |
Наглядное изображение |
|
Проекция прямой (АВ, черт. 3) на любую плоскость (V) есть прямая (ab). |
Черт. 3 |
|
Если прямая параллельна плоскости проекций, то ее проекция параллельна самой прямой.
|
|
|
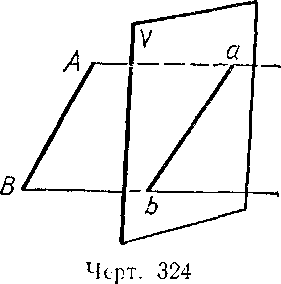
Отрезок прямой, параллельной плоскости проекций, проектируется на нее в натуральную величину.
|
Черт.4 |
|
Отрезок прямой, непараллельной плоскости проекций, проектируется на нее вообще не в натуральную величину.
|
|
|
Если отрезок (АВ, черт. 6) разделен на несколько частей (АС, СВ, . . .), то и проекция его разделится на столько же частей (ас, cb, . . .), причем части проекции пропорциональны соответствующим частям отрезка. |
|
|
Проекции параллельных прямых параллельны (черт. 7). |
|
|
Проекции пересекающихся прямых пересекаются между собой.
|
|
Сравнение проекций трех родов.
Сравнивая между собой проекции: ортогональные, косоугольные и перспективные, мы видим, что каждая из них обладает своими достоинствами и своими недостатками.
|
Проектирование |
Плюсы |
Минусы |
|
Ортогональное |
давая план, фасад, а иногда и профиль изображаемого предмета, позволяет безошибочно судить о расположении в пространстве всех частей его и об их относительном размере; |
составить себе по ортогональным проекциям ясное понятие о том, как этот предмет представлялся бы глазу, часто весьма затруднительно (иногда чертеж бывает очень сложный); |
|
Перспективное |
наоборот, дает вполне наглядное зрительное представление о предмете; |
но не указывает точных размеров его частей; |
|
Косоугольное |
уподобляясь перспективному, дает более наглядное, чем при ортогональном проектировании, представление о виде предмета и до некоторой степени позволяет судить также и о размерах его частей (если известен масштаб «сокращения»).
|
|
Ортогональные проекции имеют весьма большое значение в тех случаях, когда по данному чертежу требуется изготовить самый предмет (например, при постройке домов, мостов, машин и т. п.). Перспективное черчение употребительно в тех случаях, когда желательно, чтобы зритель, смотрящий на картину, сразу составил себе ясное представление об изображенном предмете; им пользуются в рисовании и живописи. Косоугольное проектирование полезно тогда, когда при помощи не очень сложных чертежей желают дать довольно наглядное представление о предмете и в то же время указать чертежом (хотя и приблизительно) на относительные размеры его частей. Такими чертежами иллюстрируются, например, книги по геометрии. Решим следующие задачи:
З адача
1.Изобразить
на плоскости α данный четырехугольник,
используя центральную проекцию.
адача
1.Изобразить
на плоскости α данный четырехугольник,
используя центральную проекцию.
З адача
2. Изобразить
на плоскости α данный четырехугольник,
используя косоугольную проекцию.
адача
2. Изобразить
на плоскости α данный четырехугольник,
используя косоугольную проекцию.
З адача
3. Изобразить
на плоскости α данный четырехугольник,
используя прямоугольную проекцию.
адача
3. Изобразить
на плоскости α данный четырехугольник,
используя прямоугольную проекцию.
Тема 3: Цилиндр

 Цилиндр
часто встречается в технике и в быту,
например, цилиндры двигателя, трубы,
шайбы и тому подобное. Определим, что
называется цилиндром в геометрии.
Цилиндр
часто встречается в технике и в быту,
например, цилиндры двигателя, трубы,
шайбы и тому подобное. Определим, что
называется цилиндром в геометрии.
Тело вращения – это геометрическая фигура, которую описывает плоская фигура при вращении ее около оси, лежащей в плоскости фигуры. Так цилиндр является простейшим телом вращения. Его описывает прямоугольник при вращении около своей стороны как оси. Поверхность цилиндра состоит из равных кругов в параллельных плоскостях – оснований цилиндра – и боковой поверхности. Часть цилиндрической поверхности, заключенная между плоскостями, называется боковой поверхностью, а части плоскостей, отсекаемые этой поверхностью, – основаниями цилиндра. Все вертикальные отрезки, из которых состоит боковая поверхность цилиндра, называются его образующими. Расстояние между основаниями есть высота цилиндра. Цилиндр называется прямым или наклонным, смотря по тому, перпендикулярны или наклонны к основаниям его образующие. Поверхностью прямого цилиндра называется объединение его оснований и боковой поверхности. Поверхность прямого цилиндра иногда называют также его полной поверхностью, подчеркивая этим, что она состоит из боковой поверхности и двух оснований.
О бъем
цилиндра:V
= П R2
H.
бъем
цилиндра:V
= П R2
H.
Боковая поверхность цилиндра: S = 2 П R H.
Можно предложить следующие задачи.
Задача 1. Вычислить площадь боковой поверхности стакана, если известно, что диаметр его дна d = 6см, высота h = 10см.
Задача 2. Найти вес 50м железной проволоки толщиной 4мм. Удельный вес железа 7,8 г/см3 .
Задача 3. Консервная банка имеет в диаметре 10см, а в высоту 5см. Сколько жести идет на ее изготовление?
Задача 4. Если изготовить банку той же вместимости, что и в предыдущей задаче, но с диаметром а) 5см; б) 6см, то какую высоту будет иметь банка?
Задача 5. В течении какого времени наполнится на 90% бак цилиндрической формы, если он имеет в окружности 12,56м его высота 4м и если в каждую минуту через трубку вливается 50л воды?
Задача 6. Узнать размеры десятилитровой банки цилиндрической формы, если ее высота равна диаметру основания.
 Черт.
4
Черт.
4 Черт.
5
Черт.
5 Черт.
6
Черт.
6
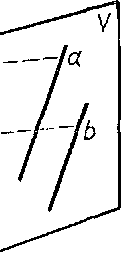 Черт.
7
Черт.
7