Файл: Геометрия в пространстве.doc

Есть веские основания предполагать, что наше пространство устроено сложнее, чем думал Евклид. Н. И. Лобачевский называл окружающее нас пространство «употребительным».

2. В геометрии существует такое понятие, как параллелограмм, который широко используется (решается масса задач на параллелограммы). Однако остается тайной, где в практике, жизни, науке используется это понятие, на изучение которого тратится много времени.

Приведем примеры, связанные с применением свойств параллелограмма в природе и технике.

Если сконструировать модель параллелограмма на шарнирах, то, меняя его угол, можно получить различные параллелограммы с теми же длинами сторон. Поэтому о параллелограмме говорят, что это – фигура «подвижная», а не «жесткая», как треугольник. Свойство подвижности параллелограмма часто используется на практике. Так, шарнирный параллелограмм применяется, например, для проведения параллельных прямых на различных расстояниях дуг от друга.

Шарнирными механизмами много и плодотворно занимался замечательный русский ученый Пафнутий Львович Чебышев (1821 – 1894). Он собственноручно изготовил много самых разнообразных механизмов, среди них – лодка с гребным аппаратом, шагающий человек («стопоходящая машина») и другие.

3. Одним из очень важных примеров применения геометрических понятий в технике и на практике является применение цилиндрической винтовой линии.

В технических приспособлениях, от самых распространенных до наиболее специальных, не обойтись без винтов, болтов, гаек, шурупов и так далее. Край резьбы у них – цилиндрическая винтовая линия.

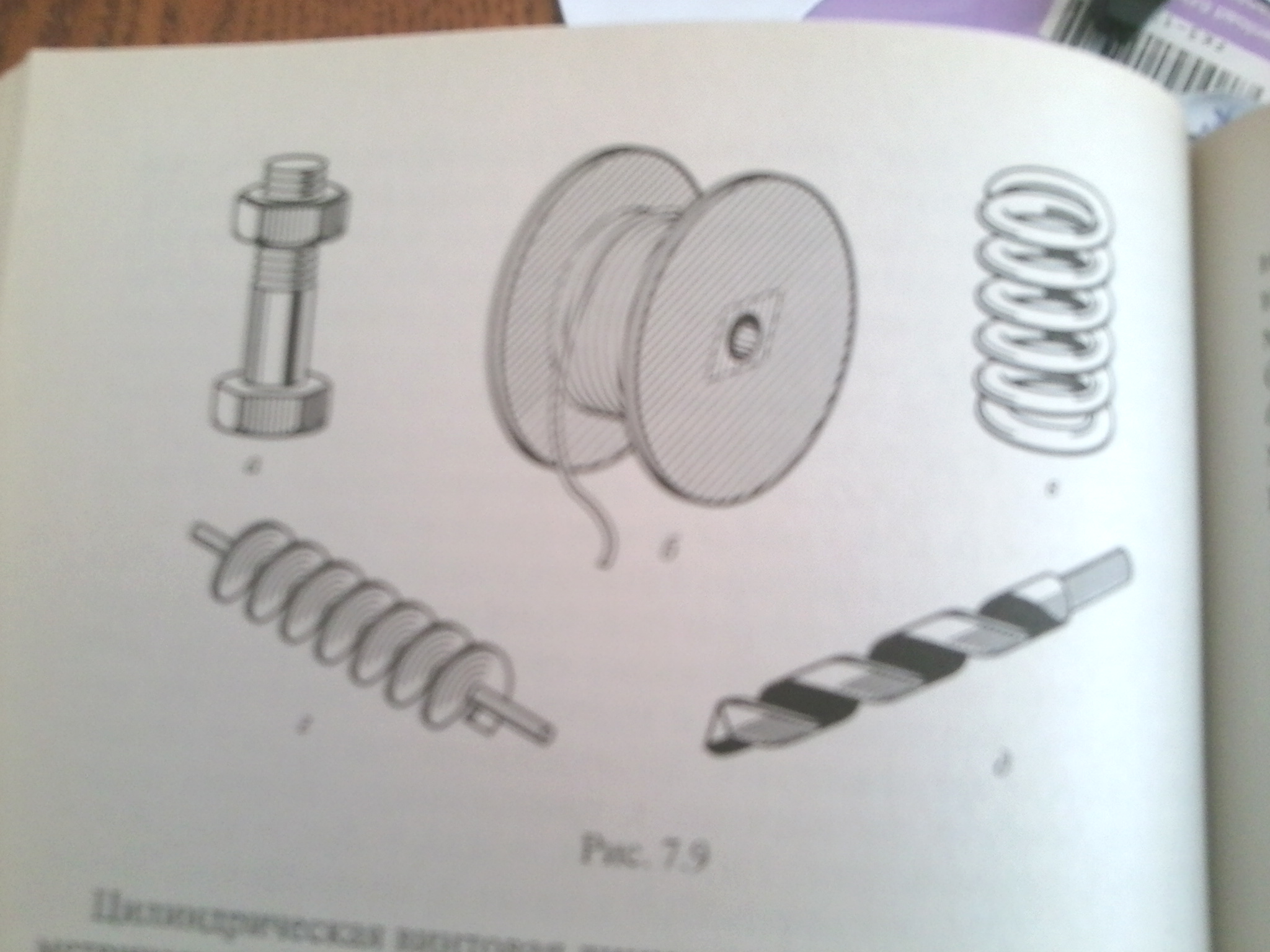
Цилиндрическая винтовая линия имеет одно удивительное геометрическое свойство – она может скользить вдоль самой себя.

Как следует понимать эти слова «скользить вдоль самой себя»?

Рассмотрим такие примеры. Прямой меч плотно, зазора входит в прямые ножны, то же относится и к мечу, изогнутому в форме дуги окружности: его всегда можно вложить в ножны той же кривизны. Именно это свойство имеют в виду математики, называя иногда прямые и окружности самосовмещающимися кривыми. При перемещении вдоль самосовмещающейся кривой любой ее дуги последняя никогда «не сходит с рельсов», то есть в любой момент времени совпадают с соответствующим участком кривой.

Можно ли придумать меч и ножны какой-нибудь другой формы, отличной от отрезка прямой или дуги окружности?

Даже после долгих размышлений многие ответят, что никакой другой формы кривой придумать нельзя, но они заблуждаются. Существует третья самосовпадающая кривая – цилиндрическая винтовая линия, или цилиндрическая спираль. Это кривая, которая, закручиваясь вдоль поверхности цилиндра, пересекает все его образующие под одним и тем же углом.

Вокруг нас есть множество примеров использования винтовой цилиндрической линии и ее свойств.

В архитектуре с помощью винтовой линии «сворачивают расстояния»: винтовая лестница занимает в строении меньше места.

Наглядное представление о винтовой линии может дать пружина. Винтовые линии очень распространены в технике. Винт, болт, гайка, сверло и многие другие предметы содержат на своей поверхности винтовые линии. Резец токарного станка при обработке цилиндрической детали, снимая стружку, описывает на ее поверхности винтовую линию.

Винтовая линия с той или иной степенью точности встречается в природе. Стебли вьющихся растений «шаг за шагом», «виток за витком» взбираются по стволу дерева по винтовой линии. По ней же смерч скручивает стволы деревьев.

Часто винтовую цилиндрическую линию называют цилиндрической винтовой спиралью.

Число витков спирали, которое необходимо сделать, чтобы перейти от нижнего листа к ближайшему верхнему, равно одному из чисел широко известного ряда Фибоначчи: 1, 2, 3, 5, 8, 13… (каждый член этого ряда равен сумме двух предыдущих). Это явление в ботанике носит название «филлотаксиса» (филлотаксис – расположение листьев); его неожиданной связи с числами Фибоначчи посвящено много книг и статей.

Стебли вьющихся растений обычно закручиваются парами, причем стебли растений-партнеров закручиваются в противоположных направлениях. Жимолость, например, всегда закручивается по левой спирали, а вьюнок – по правой.

За исключением винтов, гаек, болтов, которые по стандарту полагается делать правовинтовыми, все остальные спирали, изготовленные человеком, обычно бывают и право, и левовинтовыми – длинные винтовые конфеты, винтовые лестницы, канаты и кабели, свитые из крученых шнуров и проводов и так далее.

4. Выше мы рассмотрели цилиндрическую винтовую линию. Не меньшее значение в геометрии и особенно в окружающем нас мире имеют конические винтовые линии.

Многое о том, что говорили про цилиндрическую винтовую линию, переносится и на коническую.

Очень похоже и само построение конической винтовой линии. Точка опишет коническую винтовую линию, если она двигается равномерно по образующей конуса, а эта образующая вращается равномерно около оси конуса с постоянной угловой скоростью.

Коническую винтовую линию можно наблюдать на винтах и в архитектуре.

Конические спирали (то есть спирали, навитые на поверхность конуса), например пружины в матрасах, могут быть право и левовинтовыми.

Самыми удивительными примерами являются раковины улиток и других моллюсков, свернутые в коническую спираль. Далеко не всегда можно говорить о том, в какую сторону закручена раковина. Например, плоскую раковину наутилуса можно, подобно спиральной туманности, рассечь пополам на две одинаковые части: правую и левую. Однако существуют тысячи красивейших раковин, образующих либо правую, либо левую спираль.

В мире растений спирали встречаются на каждом шагу: в строении соцветий шишек, листьев и ветвей вокруг ствола дерева.

По спирали перемещаются не только неодушевленные предметы, но и представители живой природы: любая точка (кроме осевой) вращающегося винта самолета или парохода; белка, взбегающая вверх или спускающаяся вниз по дереву; стаи летучих мышей, вылетающих из поземных пещер. В качестве примеров конической спирали можно привести водовороты, воронки ураганов, траекторию точек воды, стекающей по желобу, и тысячи других явлений природы [9, с. 238-254].

Было рассмотрено только несколько фрагментов, показывающих связь геометрических знаний с закономерностями окружающего мира. Конечно, весь этот материал не может быть изучен со всеми учащимися на уроках геометрии. Часть его предназначена для самостоятельного чтения и изучения. Практика показывает, что такой материал очень интересен и полезен для учащихся.