ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.04.2024
Просмотров: 135
Скачиваний: 0
Тема 8: Вычисление площадей и объемов геометрических тел
Используя ранее полученные знания, приступаем к решению задач, пользуясь следующими формулами.
Объем прямоугольного параллелепипеда с линейными размерами a, b, c: V = a b c.
Объем любой призмы равен произведению площади основания на высоту призмы.
Объем пирамиды равен одной трети произведения площади основания на высоту пирамиды.
Объем усеченной пирамиды равен разности объемов полной пирамиды и осекаемой от нее подобной пирамиды.
Объемы подобных тел относятся как кубы их соответствующих размеров.
Площадь сферы радиуса R: S = 4 П R2.
Площадь сферического сегмента радиуса R и высотой H: S = 2 П RH.
Объем шара: V = 4/3 П R3.
Объем цилиндра: V = П R2 H.
Боковая поверхность цилиндра: S = 2 П RH.
Площадь боковой поверхности конуса: S = П R l, где l – длина образующей конуса.
Объем конуса: V = 1/3 П R2 H
Задача 1. Золотой жетон весит 7г. Он имеет форму четырехугольной призмы. Диагональ основания призмы 16мм. Узнать ширину этого жетона. Удельный вес золота 19,3г/см3.
Задача 2. Медный жетон весом 17г имеет форму правильной шестиугольной призмы. Сторона основания призмы 8мм. Вычислить толщину этого жетона. Удельный вес меди 7,8г/см3.
Задача 3. В стеклянный кубический сосуд надо налить воды так, чтобы ее объем составлял 2/3 объема сосуда. Как это сделать, ничего не измеряя?
Задача 4. Прямоугольный параллелепипед имеет ребра длиной 1, 2, 3.
Возьмите любые две скрещивающиеся диагонали соседних его граней и вычислите расстояние между ними, используя формулы объемов.
Задача 5. Основанием прямой призмы является пятиугольник, в котором три последовательных угла прямые и два равные тупые. Длины всех ее ребер известны. Из нее хотят вырезать прямоугольный параллелепипед наибольшего объема. Основание его лежит в основании призмы. Как это сделать?
Задача 6. Все грани треугольной пирамиды – равные равнобедренные треугольники. Высота пирамиды лежит в одной из граней. Расстояние между наибольшими боковыми ребрами равно d. Найдите объем пирамиды.
Задача 7. Из куба вам требуется сделать правильную пирамиду наибольшего объема. Как вы будете действовать, если нужна: а) треугольная; б) четырехугольная; в) шестиугольная пирамида?
Задача 8. В кубе расположено шесть пирамид. Вершина каждой из них находится в центре одной из граней. А основание каждой совпадает с гранью куба, параллельной той, где взята вершина. Какую часть от объема куба составляет объем пересечения этих пирамид?
Задача 9. Дана правильная треугольная призма. На двух скрещивающихся диагоналях ее боковых граней находятся вершины правильного тетраэдра. Найдите отношение объема тетраэдра к объему призмы.
Задача 10. Два шара радиусами R1 и R2 пересекаются. Найдите объем их общей части, если расстояние между их центрами равно d.
Задача 11. Дан правильный тетраэдр с ребром 1. Найдите различные варианты укладки четырех равных шаров внутри его. В каком из них суммарный объем этих шаров будет больше?
Задача 12. Известны объемы вписанного и описанного шаров для: а) цилиндра; б) конуса; в) правильного тетраэдра. Можно ли по этим данным найти объемы самих многогранников?
Задача 13. Дан полушар. Какую часть от его объема составляет наибольший объем находящихся в нем: а) прямоугольного параллелепипеда; б) правильной треугольной призмы; в) правильной четырехугольной пирамиды.
Задача 14. Дан шар радиусом 1. Чему равен наибольший объем расположенного в нем тела, являющегося объединением цилиндра и конуса с общим основанием?
Задача 15. Корыто имеет форму полуцилиндра. Его емкость равна V, толщина стенок равна h, плотность материала, из которого оно сделано, равна r. Каким надо выбрать его размеры, чтобы его масса была: а) наименьшей; б) наибольшей?
Задача 16. Стог сена имеет форму цилиндра с коническим верхом. Радиус его основания 2,5м, высота 4м, причем цилиндрическая часть стога имеет высоту 2,2м. Плотность сена 0,03г/см3. Определить массу стога сена.
Задача 17. Сечение железнодорожной насыпи имеет вид трапеции с нижним основанием 14м, верхним 8м и высотой 3,2м. Найдите, сколько кубических метров земли находится на 1км насыпи.
Задача 18. Измерения прямоугольного бруска 3см, 4см, 5см. Если увеличить каждое ребро на x сантиметров, то поверхность увеличится на 54см2. Как увеличится объем?
Задача 19. Три латунных куба с ребрами 3см, 4см, 5см переплавлены в один куб. Какое ребро у этого куба?
Задача 20. Колечко ограничено цилиндрической и сферической поверхностью. Как найти его объем?
Приложение Это интересно
Курс геометрии в школе должен способствовать осознанию всеми учащимися общей картины мира, устройства возможностей его познания с использованием геометрических знаний. Материал курса геометрии развивает представления учащихся, полученные ими в начальной школе, и позволяет совместно с другими естественнонаучными дисциплинами познавать окружающий мир.
Это осуществляется следующим образом:
В самом начале изучения геометрии в пятом классе происходит первое знакомство с понятием пространства. Конечно, на этом этапе обучения сказать можно не так уж и много. Вот некоторые фрагменты.
Все, что нас окружает, называется пространством. Каждый человек живет в пространстве. В пространстве расположено множество различных объектов: планета Земля, другие планеты солнечной системы, звезды и созвездия различных галактик, горы на поверхности Луны и так далее.
Геометрия изучает также пространство, в котором расположены различные геометрические фигуры: треугольники, круги, пирамиды, шары, кубы и другие.
Многие предметы в окружающем нас мире имеют аналоги в геометрии, то есть геометрические фигуры в геометрии – модели объектов реальной природы: пирамиды Древнего Египта и пирамиды в геометрии, жилые дома вокруг нас и прямоугольные параллелепипеды в геометрии и так далее.
Все планеты Солнечной системы представляются нам шарообразными телами.
Так, планета Земля с точки зрения геометрии рассматривается как шар, диаметр которого приблизительно равен 12 800 км, радиус – 6400 км. Диаметр шара – отрезок, соединяющий любые две точки поверхности шара и проходящий через его центр. Половина диаметра называется радиусом. Размеры шаров, а, следовательно, и планет принято сравнивать по длине радиусов.
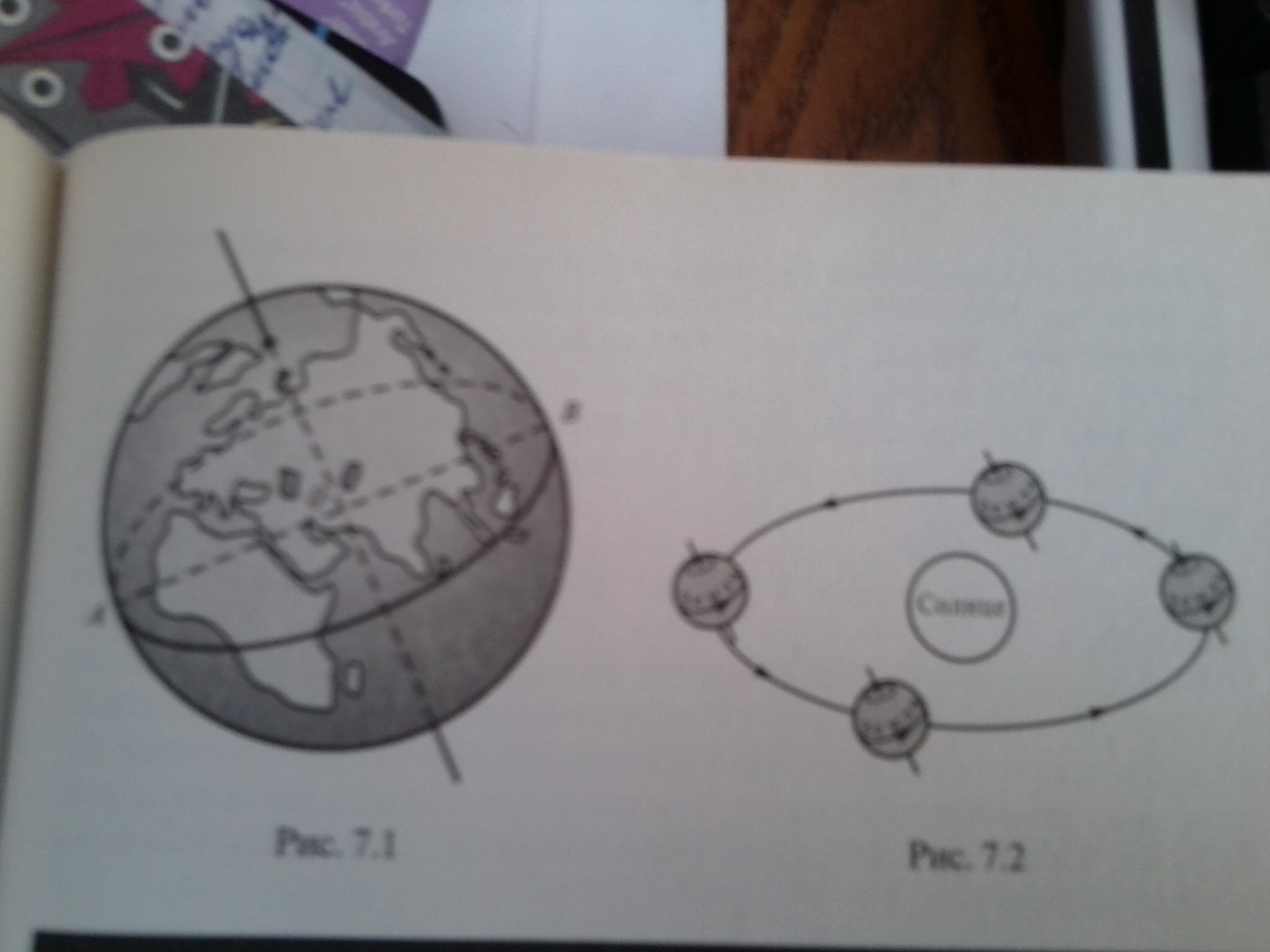
Поверхность шара называется сферой. С точки зрения геометрии поверхностью Земли и других планет являются сферы.
Земля движется вокруг Солнца по почти круговой орбите, радиус которой равен 150 000 000 км. При этом диаметр Солнца более чем в 100 раз больше диаметра Земли и равен 1 390 000 км. Луна тоже представляется нам шарообразным телом, ее диаметр почти в 4 раза меньше диаметра Земли, он равен приблизительно 3500 км.
Итак, есть пространство, в котором мы живем и пространство, которое изучается в геометрии (евклидово пространство).
Человечество в процессе своего развития потратило много сил на изучение закономерностей окружающего мира и на создание геометрии, которую изучаем в школе. Но чем больше ученые занимались этими проблемами, тем чаще появлялись многочисленные сложные вопросы.
Верно ли, что пространство, в котором мы живем, устроено как пространство, которое изучаем в курсе школьной геометрии? Евклидово ли оно? Выполняются ли в нашем реальном пространстве законы геометрии Евклида?
Казалось бы, ответы очень просты, так как законы евклидовой геометрии очевидны: «Через две точки проходит только одна прямая», «Каждая прямая бесконечна в обе стороны», «Перпендикуляр и наклонная к одной прямой непременно пересекаются».
Кажется, все это так и иначе быть не может! Об этом говорил и знаменитый немецкий философ И. Кант: «Иначе мыслить нельзя!». Но вот великий наш соотечественник Н. И. Лобачевский показал, что прекрасно можно думать иначе! Он построил геометрию, в которой все аксиомы Евклида выполняются, кроме одной – аксиомы параллельных. Оказалось, что его геометрия не только не хуже евклидовой, но в некоторых отношениях даже совершеннее ее, богаче.
Возникают и другие вопросы: можно ли вообразить, что прямая имеет конечную длину; разве кто-нибудь уходил по прямой так далеко, что убедился в ее бесконечности; быть может, если уйдем по прямой очень-очень далеко, то вдруг окажемся в исходной точке путешествия?
Именно так и произошло бы с человеком, который, полагая, что Земля – плоская, отправился в некотором направлении, стараясь все время идти по кратчайшей линии; думая, что идет по прямой, и вдруг пришел бы в начальную точку путешествия.
Может быть, зря думаем, что прямая бесконечна, а она является замкнутой линией вроде окружности, только очень большой длины? В истории развития человечества было много ясных вещей, которые потом оказались просто неверными. Ведь все считали (пока люди не доказали, что Земля – шар), что вертикали, проведенные к поверхности Земли, строго параллельны, а оказалось, что они пересекаются в центре Земли. Спутники Магеллана думали, что если они будут аккуратно каждый день делать записи в судовом журнале, то, объехав вокруг света и вернувшись домой, не ошибутся в счете дней. А все же оказалось, что один день пропал.