ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.04.2024
Просмотров: 109
Скачиваний: 1
СОДЕРЖАНИЕ
8 Вычислить определенный интеграл
9 Исследовать сходимость рядов
10 Исследовать ряды на сходимость
14 Вычислить криволинейный интеграл
26. Решить первую краевую задачу для уравнения теплопроводности:
28.Найти изолированные особые точки аналитической функции и выяснить их характер:
30. Решить интегральное уравнение
Найти методом моментов точечные оценки неизвестных параметров а и s нормального распределения.
Решение:
формулы методов моментов имеют вид:
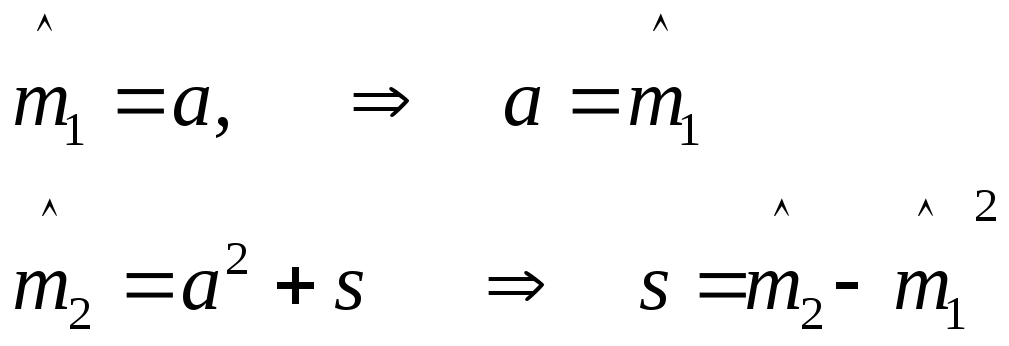
![]() ,
,
![]()
все подсчеты запишем в таблицу, после чего вычислим значение параметров
|
|
|
|
|
|
|
|
|
6 9 26 25 30 26 21 24 20 8 5 |
0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,2 2,3 |
0,072 |
0,228 0,428 0,628 0,828 1,028 1,228 1,428 1,628 1,828 2,128 2,228 |
0,052 0,183 0,394 0,686 1,057 1,508 2,039 2,650 3,342 4,528 4,964 |
|
|
200 |
14,4 |
|
|
21,403 |
![]()
![]()
![]()
33. ЭВМ может находиться в одном из следующих состояний: S1 – исправна, работает; S2 – неисправна (остановлена) и идет поиск неисправности; S3 – неисправность обнаружена и идет ремонт; S4 – ремонт закончен и идет подготовка к пуску. Известно: среднее время безотказной работы ЭВМ равно 24 часам; для ремонта её приходится останавливать в среднем на 4 часа; поиск неисправностей длится в среднем 0,4 часа; подготовка к пуску занимает 2 часа. Вычислить предельные вероятности состояний рассматриваемой системы.
Решение:
S1 – исправна, работает;
S2 – неисправна (остановлена) и идет поиск неисправности;
S3 – неисправность обнаружена и идет ремонт;
S4 – ремонт закончен и идет подготовка к пуску.
составим цепь Маркова

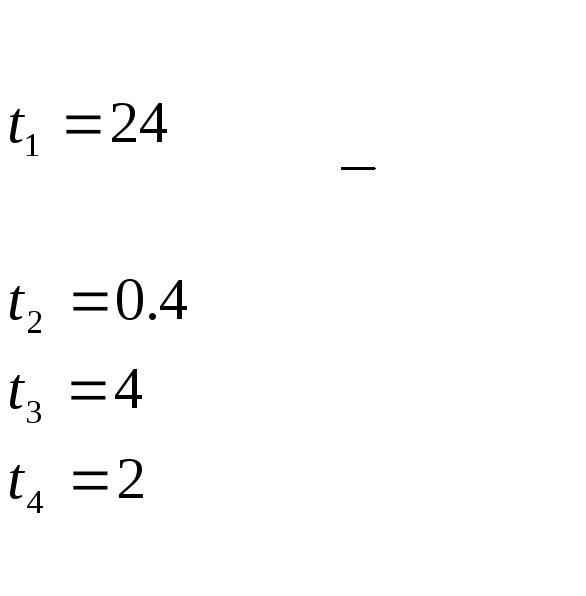
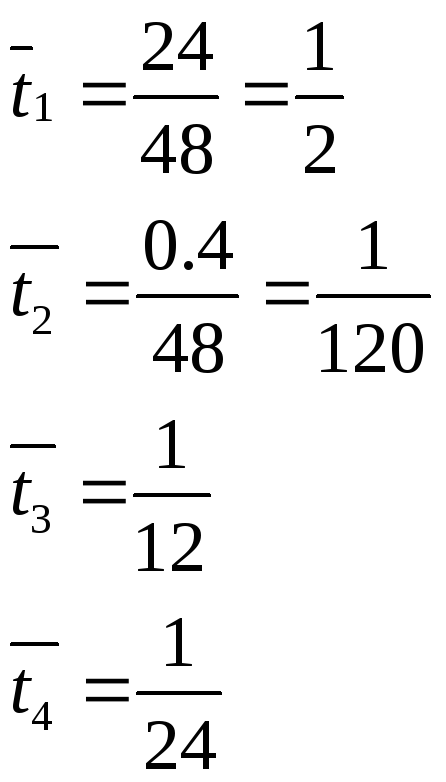
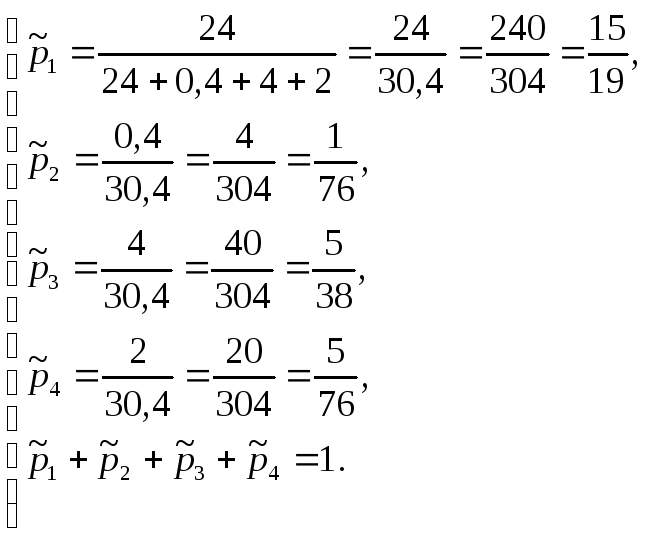
34. Из 25 студентов группы 5 студентов знают все 30 вопросов программы, 10 студентов выучили по 25 вопросов, 7 студентов по 20 вопросов, трое по 10 вопросов. Случайно выбранный студент ответил на два заданных вопроса. Какова вероятность, что он из тех трех студентов, которые подготовили 10 вопросов.
Решение:
найти р из 25 трое.
Воспользуемся классическим опр
вероятности
![]() ,
,
