Файл: Матан(3блок).doc

1 Вычислить пределы

А)

Решение

Б)

Решение

В)

Решение

Б.3 В.2 Определить наибольшее и наименьшее значения ф-ии в области. Область задания ф-ии представляет собой треугольник ограниченный координатными осями и прямой.

Найдем стационарные точки внутри области здания функции:

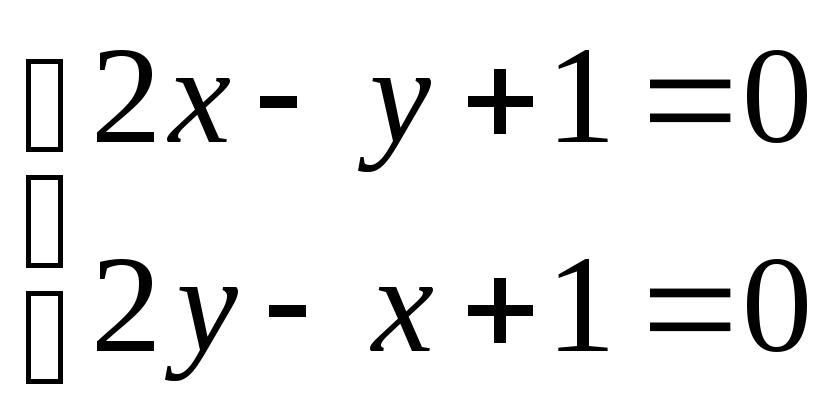x = -1 y = - 1

Получили точку (-1;-1). Других стационарных точек нет. (-1;-1) принадлежит данной области, найдем значение функции в этой точке

Z(- 1, - 1)= -1.

Исследуем ф-ию на границе области. Поскольку граница состоит из трех участков, описанных тремя разными уравнениями исследуем ф-ию на каждом участке отдельно.

а) ОА, А(-3,0) . уравнение связи y=0. С учетом уравнения связи ф-ия представляется в виде, тогда

Стационарная точка: (-1/2,0). Значение функции в ней z(-1/2,0)=-1/4 -1/2=-1/4.

---

б) ОВ, В(0,-3)

Уравнение связи: х=0

С учетом его ф-ия имеет вид , тогда

y=-1/2

Стационарная точка (0,-1/2), значение ф-ии в ней z(0,-1/2)=1/4-1/2=-1/4

в) исследуем функцию вдоль участка прямой .

Подставляя в выражение для ф-ии, получим

Тогда

следовательно х=-3/2, y=-3/2.

Стационарная точка (-3/2,-3/2). Значение функции в ней z(-3/2,-3/2)=-3/4.

Вычислим значения функции в точках О, А, В.

z(0,0)=0; z(-3,0)=9, z(0,-3)=9.

Сравнивая значения заключаем: 9- наибольшее значение функции, достигаемое в точках (-3,0) и (0,-3); -1 – наименьшее значение функции, достигаемое внутри области в точке (-1,-1).

Б.3 В.3

Найдем точки пересечения параболы и прямой:

А(-2,4), В(2,4)

Найдем стационарные точки внутри области задания ф-ии

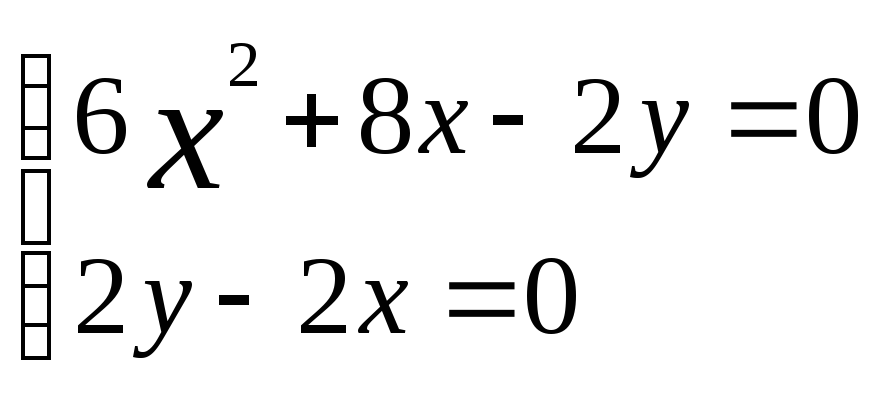
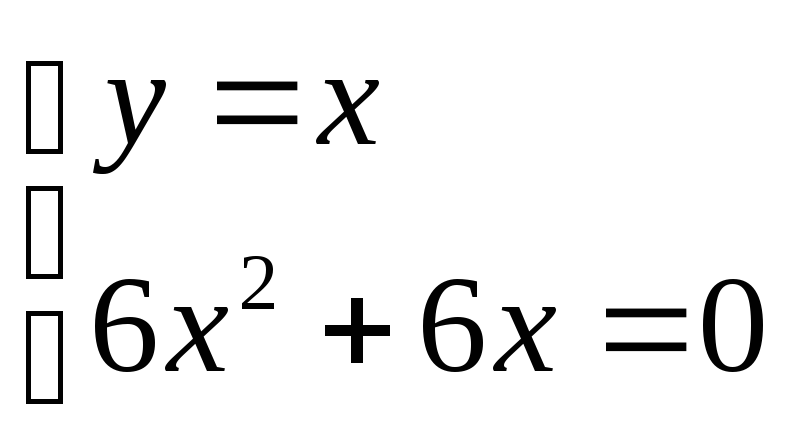
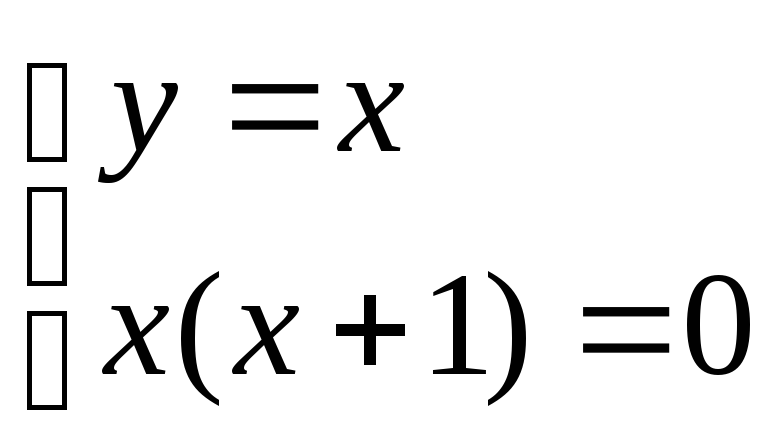
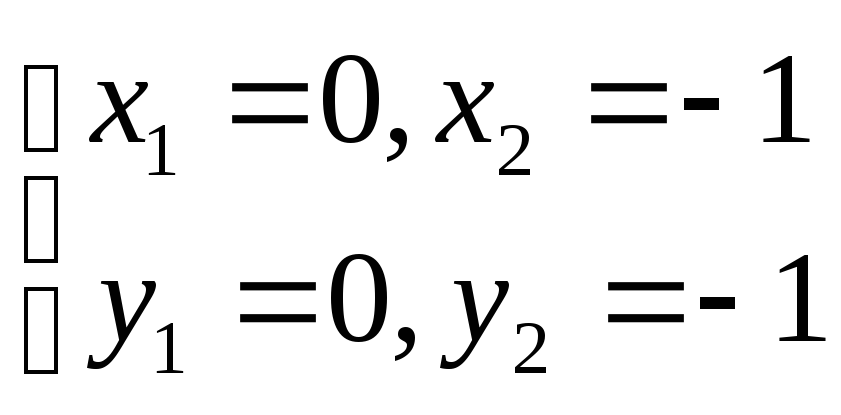
получили две точки (0,0) и (-1,-1). Точка (-1,-1) не принадлежит рассматриваемой области. Найдем значение ф-ии в точке (0,0): .

---

Исследуем ф-ию на границе области.

Исследуем вдоль участка. Подставляяв выражение для функции получим:, тогда

точку (0,0) уже рассматривали.

Исследуем вдоль участка y=4

стационарные точки (-2,4) и (2/3,4). Значения ф-ии в этих точках: .

Исследуем в точках В(2,4).

Сравнивая значения заключаем: 32 – наибольшее значение ф-ии достигаемое в точках (-2,4) и (2,4); 0 – наименьшее значение ф-ии, достигаемое в точке (0,0).

Б.3 В.4 Найти наибольшее и наименьшее значение ф-ии в данной области

Область задания ф-ии представляет собой треугольник ограниченный прямыми:

Найдем стационарные точки внутри области задания ф-ии

---

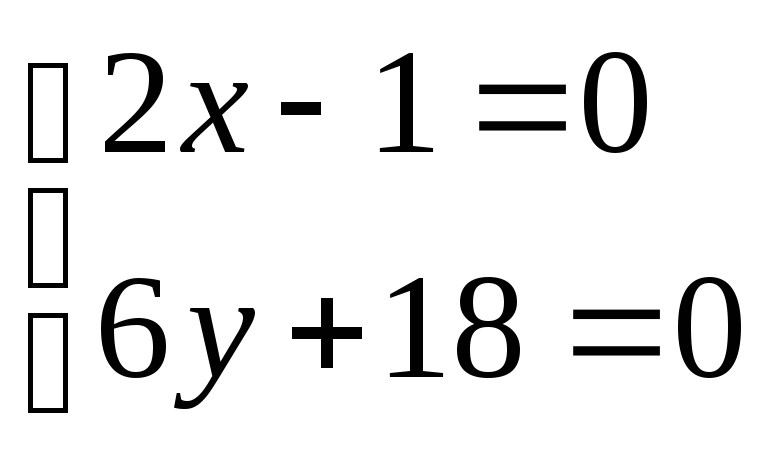x=1/2 y= - 3

получили точку (1/2, -3) которая не принадлежит рассматриваемой области, поэтому ее не рассматриваем.

Исследуем ф-ию на границе области. Поскольку граница состоит из трех участков, описанных тремя разными уравнениями то исследуем ф-ию на каждом участке отдельно.

1) ОВ, В(0,4). Уравнение связи x=0. ф-ия с учетом уравнения связи имеет вид:

точка (0,-3) не принадлежит рассматриваемой области.

2) y=4. Функция принимает вид

Стационарная точка (1/2,4). Значение ф-ии в ней

3) ОА, А(4,0) уравнение связи y=x. Ф-ия принимает вид:

точка (-17/8,-17/8) не принадлежит рассматриваемой области.

4) Рассмотрим точки О(0,0), А(4,0), В(0,4)

,

Сравнивая значения заключаем: 116 – наибольшее значение, достигаемое в точке (0,4), -4 – наименьшее значение достигаемое в точке (0,0).

5 найти дифференциал второго порядка ф-ии z=y ln x

Решение

---

6 найти производную сложной ф-ии u=ln(x^2+y^2) x=st y=s/t

Решение

u=f(x,y) x=x(s,t) y=y(s,t)

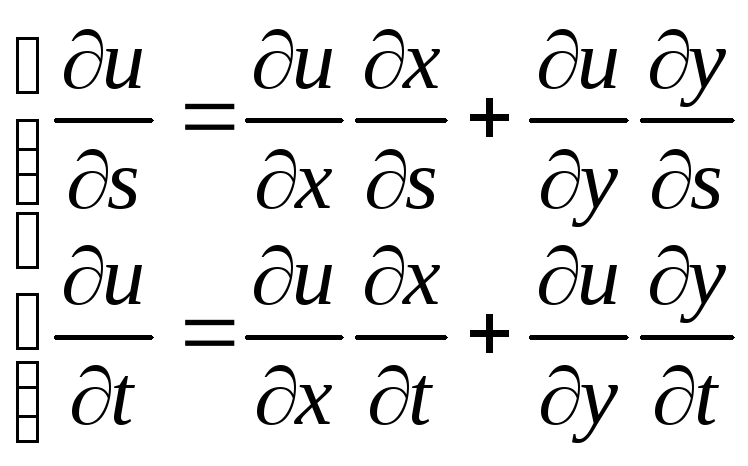
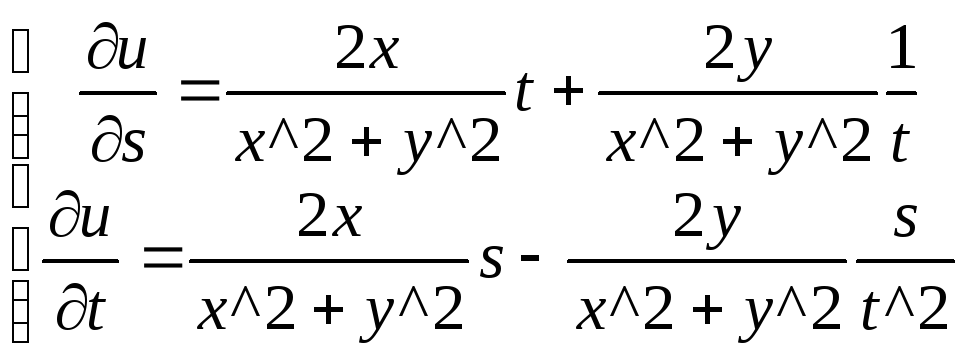
Полный дифференциал представится в виде

7 найти d^3z если z=e^x cos y

Решение

---