Файл: Матан(3блок).doc

Разложение не содержит отриц степеней z, следовательно точка z=0 является устранимой точкой.

29. Найти вычеты функции

А) , Б), В).

****теория****

1) В случае когда z=a- устранимая точка

2) Если z=a – полюс функции f порядка р , то

(1)

В частности при р=1 (1) примет вид: (2)

3) Пусть функция f в окружности простого полюса z=a имеет вид: (3, где - аналитические в точкеz=a ф-ции, причем Имеем

(4)

4) Теорема Пусть , тогда сумма вычетов функцииf во всех ее конечных особых точках и вычета на бесконечности равна:

(5)

Решение: А)

Особыми точками данной функции являются . Данные точки являются простыми полюсами, поэтому применим формулу

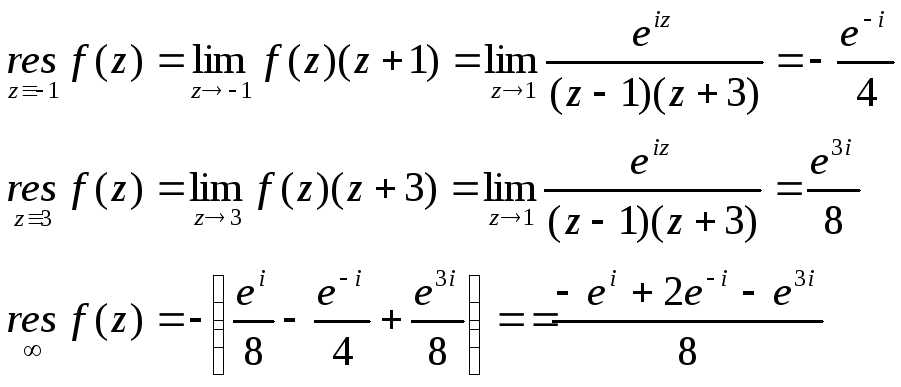
Б)

Особыми точками данной функции является .

Точка является полюсом первого порядка функцииf, поэтому для вычисления вычета в этой точке применим формулу , получим

---

Аналогично

Согласно формуле имеем

Следовательно

В) В точках данная функция имеет простые полюсы. Воспользуемся функцией, в которой.

Тогда

.

Бесконечно удаленная точка является предельной для особых точек.

---

30. Решить интегральное уравнение

А) ;

Решение:

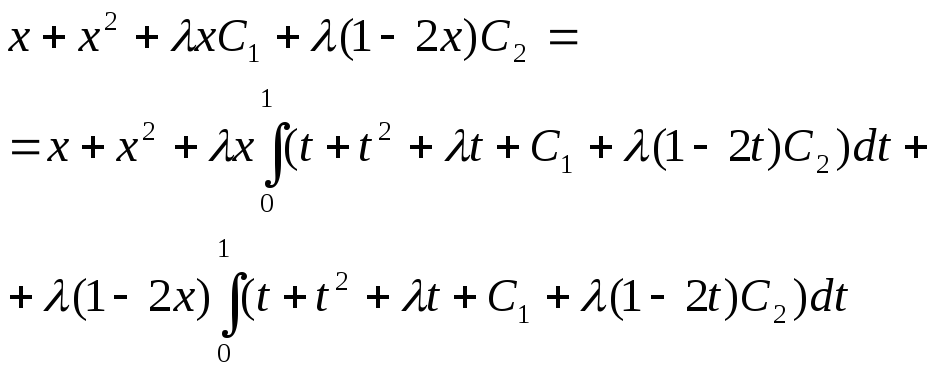
Делая подстановку и решая систему, получаем

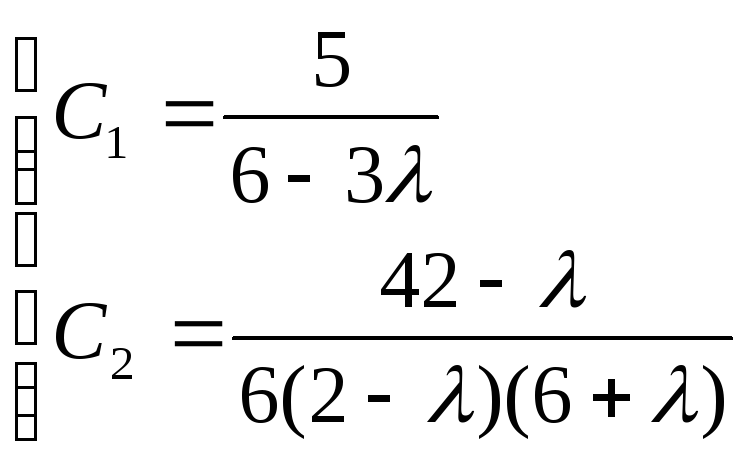
Подставляем в исходное равенство

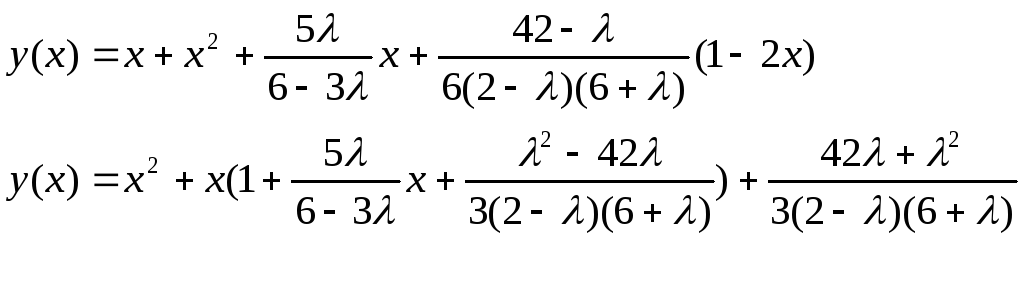После упрощение(в скобках приведете к одному знаменателю сами), получаем

, следовательно

Ответ: 1) , если

2) если

30. Решить интегральное уравнение

Б)

Из таблицы оригиналов и изображений имеем ,

Подставим изображения в исходное уравнение, получим:

Разложим получившееся выражение на простые дроби

Домножим левую и правую часть равенства на знаменатель

---

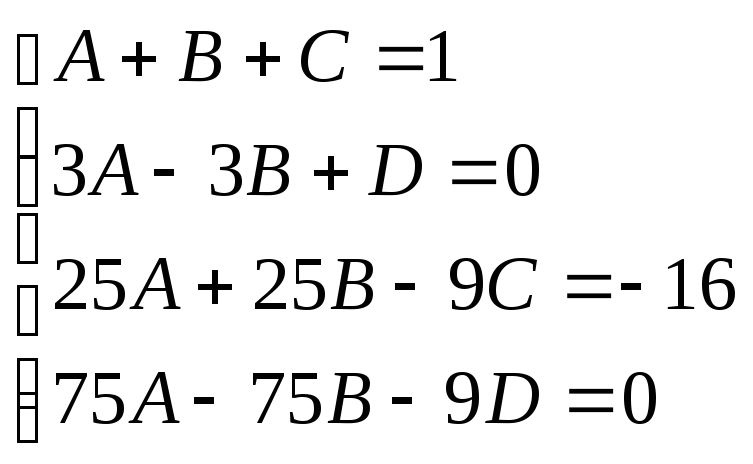
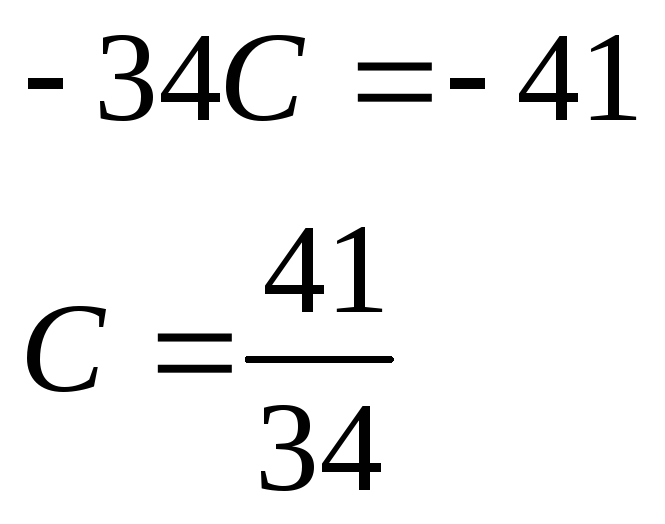
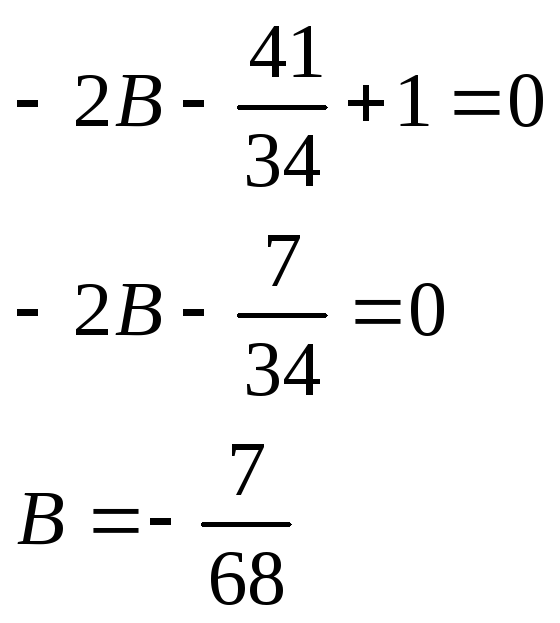
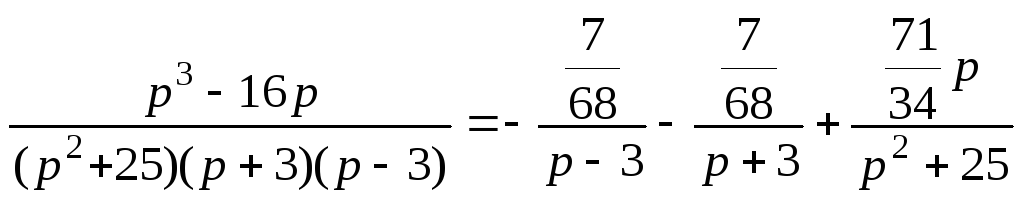
Из таблицы оригиналов и изображений получаем

Ответ: .

31. Методом малого параметра найти три члена разложения (по степеням малого параметра µ) решения уравнения

Решение: так как правая часть является аналитической функцией переменных при у>0, то решение ищем в виде:

(1)

Очевидно, что

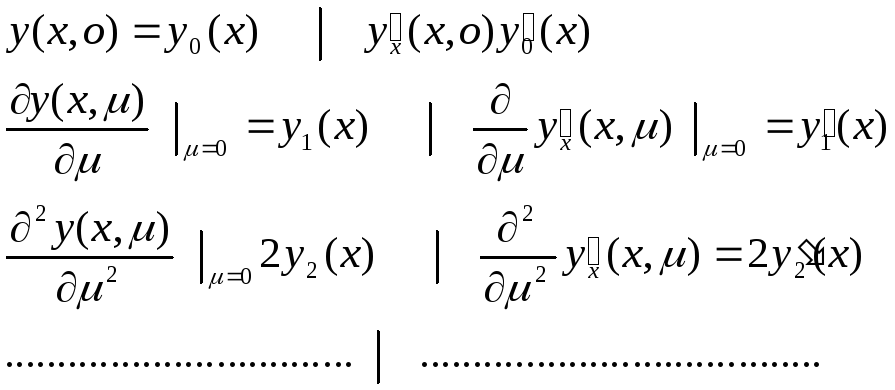
Подставим в уравнение

Положим (2)

Исходя из начального условия

---

Из (2)

Дифференцируем по параметру наше уравнение

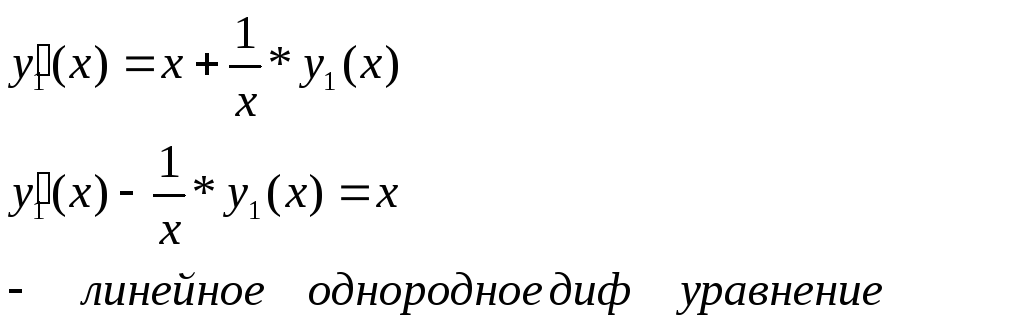
Варируем const

Но

Дифференцируем по параметру:

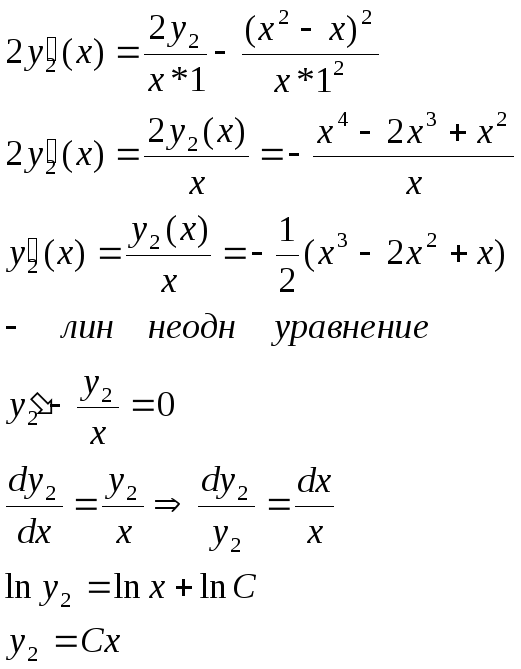
Варируем const

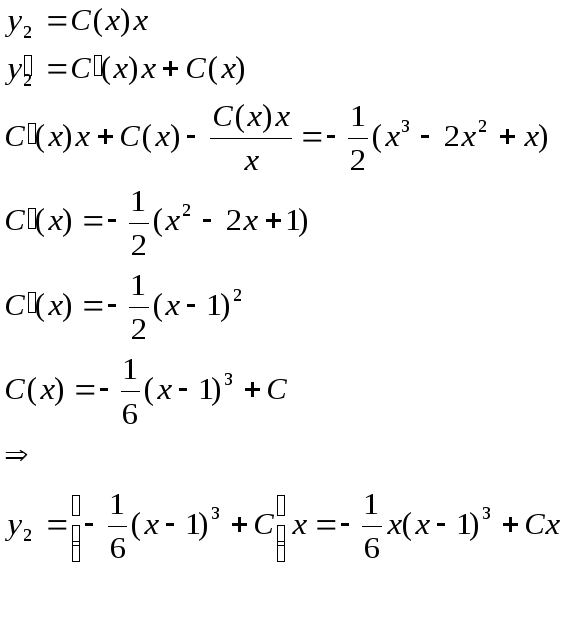
Так как

Значит

И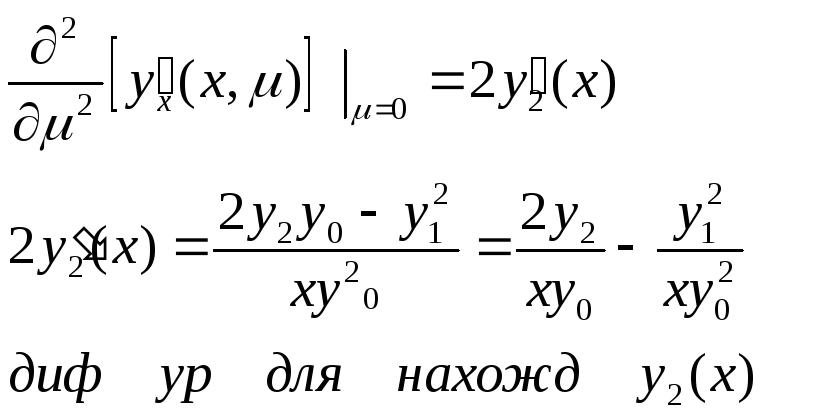так

32. Случайная величина ξ (отклонение контролируемого размера изделия от номинала) подчинена нормальному закону распределения с неизвестными параметрами а и s. Ниже приведена таблица наблюдаемых отклонений от номинала, подвергнутых группировке, для п=200 изделий (х_i – середины интервалов отклонений; n_i – число наблюдений, попадающих в данный интервал):

хiя	0,3	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9	2,2	2,3
n i	6	9	26	25	30	26	21	24	20	8	5

---