Файл: Матан(3блок).doc

---

8 Вычислить определенный интеграл

А)

Решение

Выделим полный квадрат в знаменателе

x^2+3x+2=(x+3/2)^2-1/4

сделаем подстановку x+3/2=t dt=dx

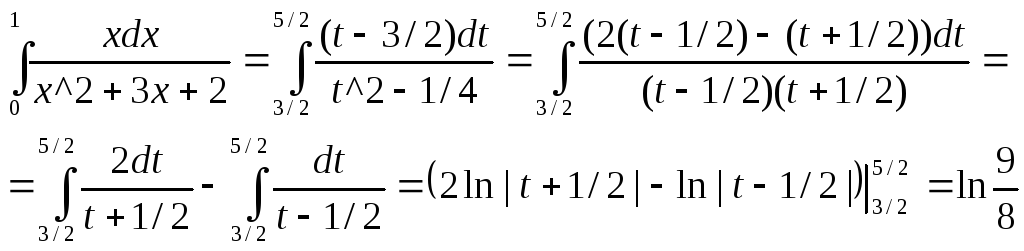
Б)

Решение

сделаем замену t=cosx dt=-sinxdx

В)

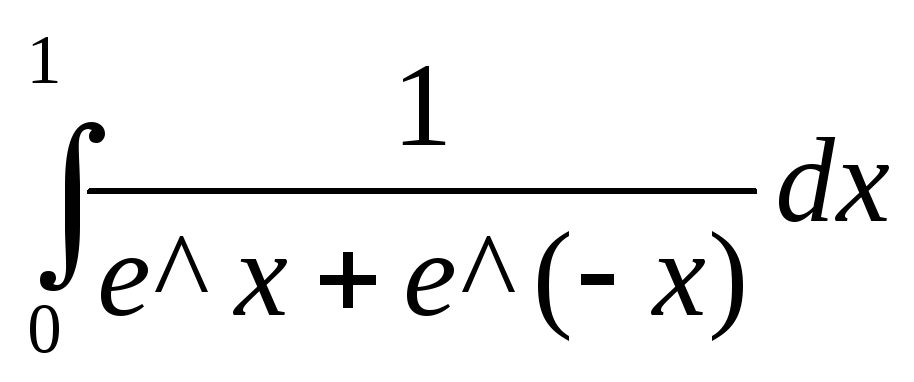
Решение

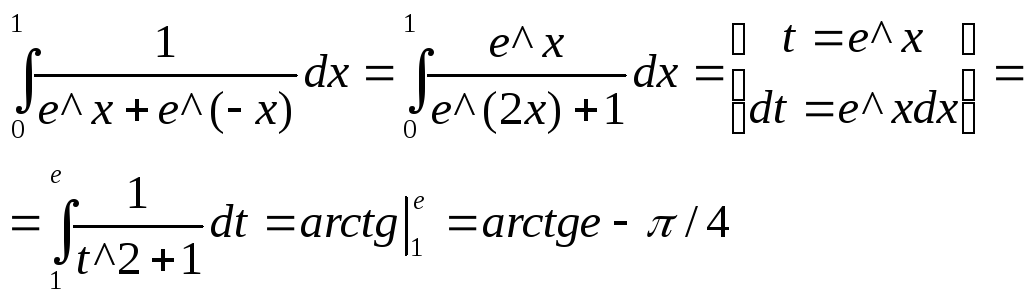
9 Исследовать сходимость рядов

А)

Решение

Все члены ряда монотонно убывают по абсолютной величине, общий член ряда стремится к нулю => ряд сходится по признаку Лейбница

б)решение

признак Даламбера то сходится

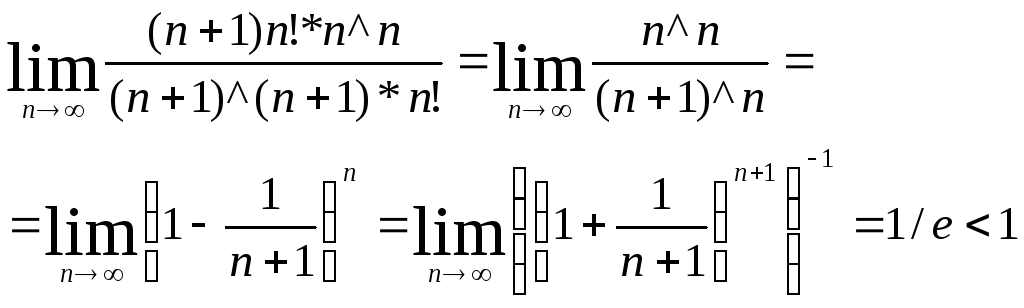В) Решение

Члены данного ряда являются значениями ф-ии ln(1+1/x)-положительная, напрерывная, неубывающая на Вычислим

=>ряд расходится

10 Исследовать ряды на сходимость

А)

Решение

---

След ряд сходися на интервале (-2,2)

При х=2 получаем гармонический ряд

При х=-2 ряд сх по признаку Лейбница

Б)

Решение

Ряд сх на интервале (-4,4)

-------------------------------------------------------------------------------------

11 разложить в ряд Фурье ф-ию f(x)=|x| на промежутке (-1,1)

Решение

Т.к. ф-ия четная то

b_n=0

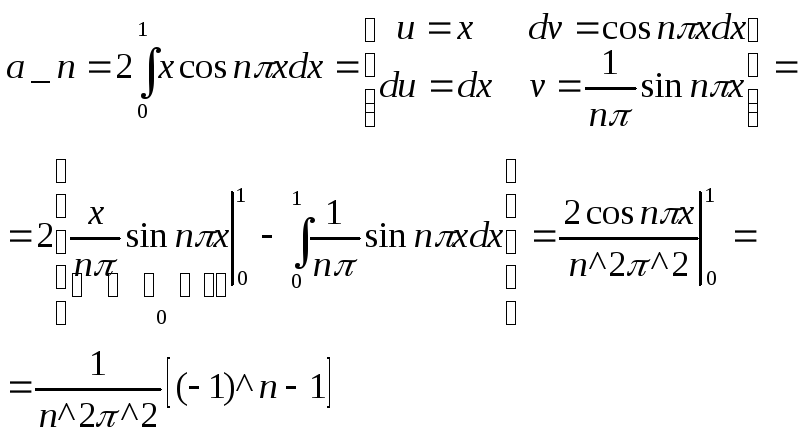
Тогда

Б.3 В.12 Разложить в тригонометрический ряд ф-ию f(x)= в [0,2].

Продолжим ф-ию четным образом на симметричный отрезок.

.

---

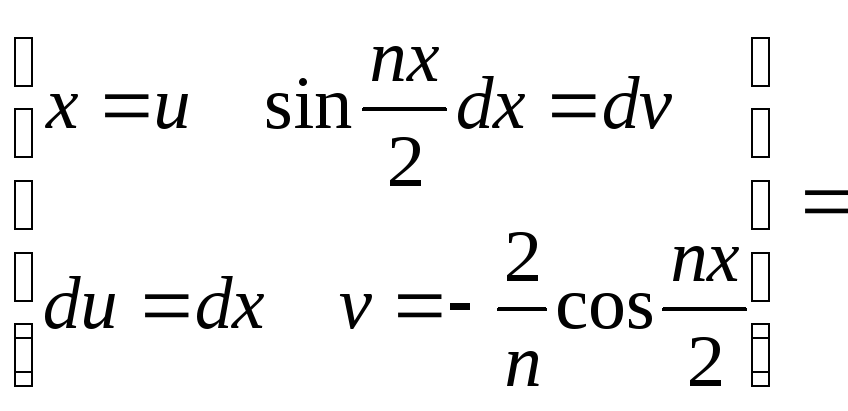
13 разложить в ряд Фурье ф-ию f(x)=sin(x/2) в [-] и построить график суммы полученного ряда

Решение

Т.к. фкция нечетная то a_n=0

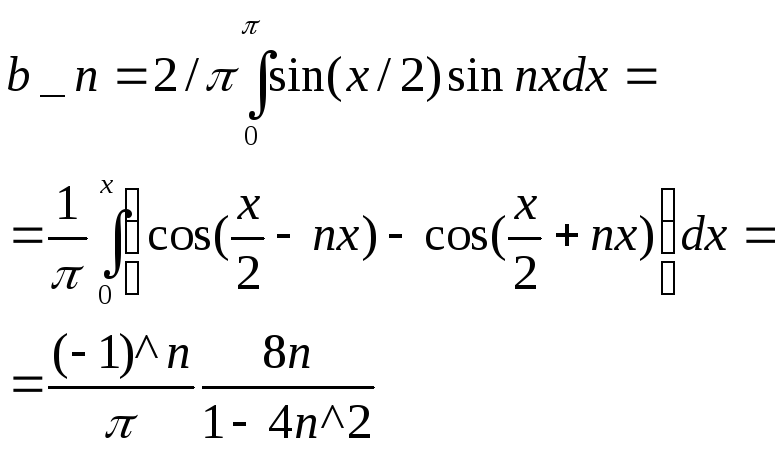
Т.о. ряд Фурье данной ф-ии

График

14 Вычислить криволинейный интеграл

где

Решение

Имеем

x^2=cos t y^2=sin t

По формуле

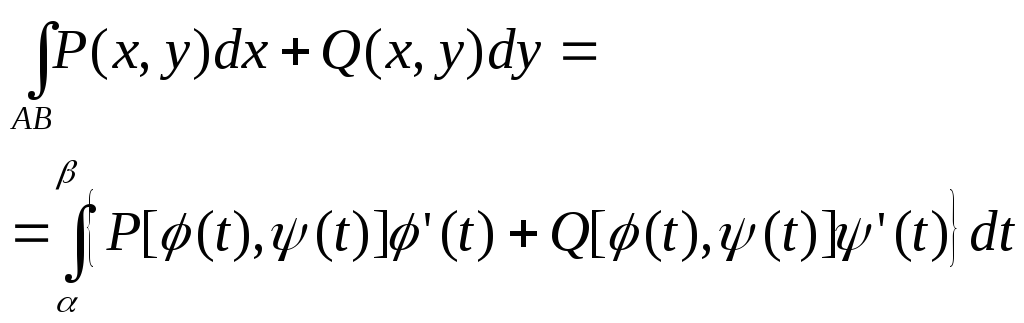
Получаем

15 вычислить криволинейный интеграл

от точки (0,0) до точки (1,2)

по кривым

а)y=2x б)y=2x^2 в)y=2

решение

по формуле

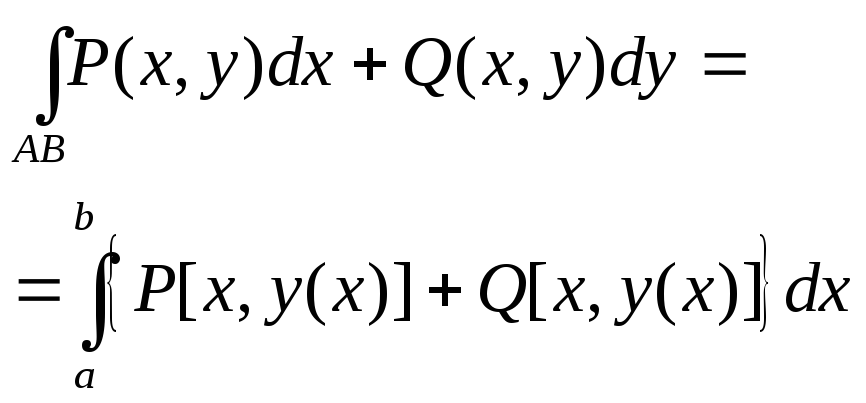
А)

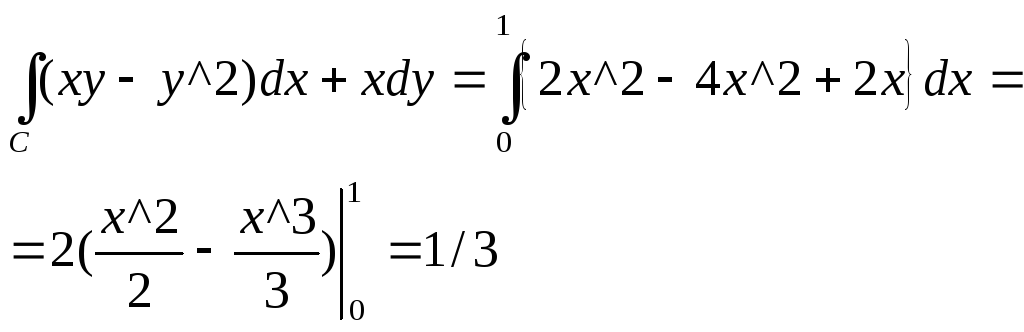
Б)

В)

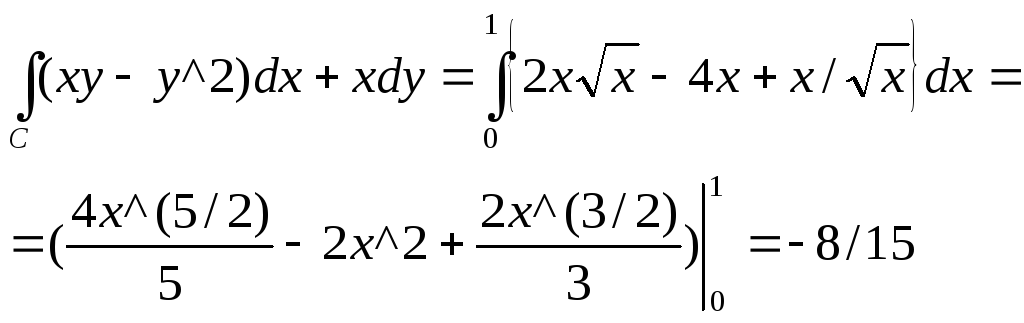
16. Решить систему

---

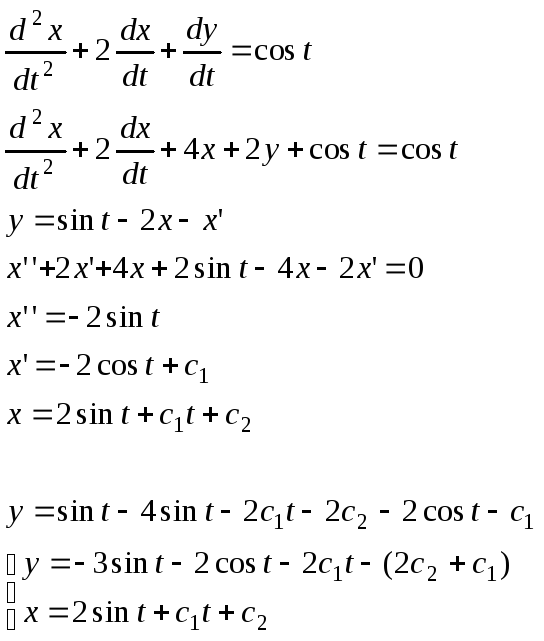
17. Решить систему методом Эйлера

Составим характеристическое уравнение

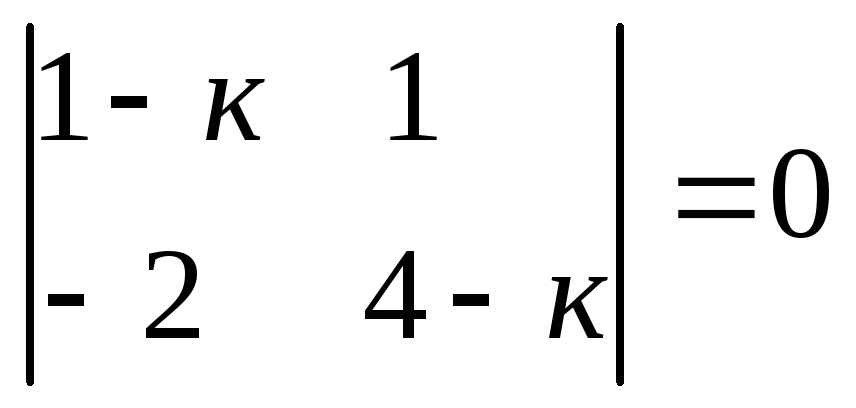
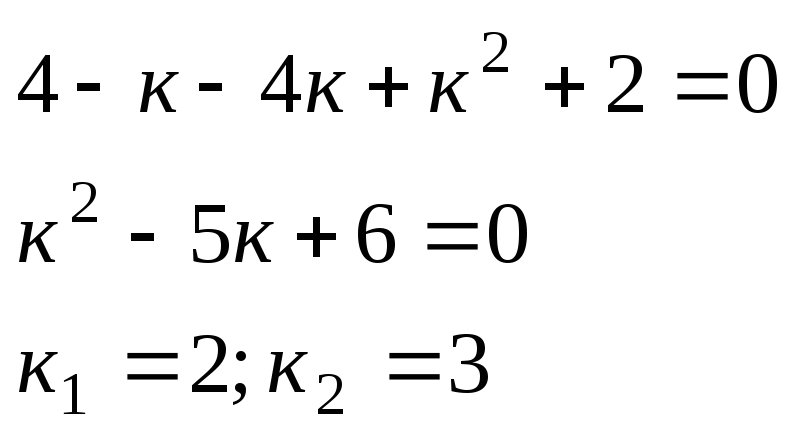
. Пусть тогда

. Следовательно ,

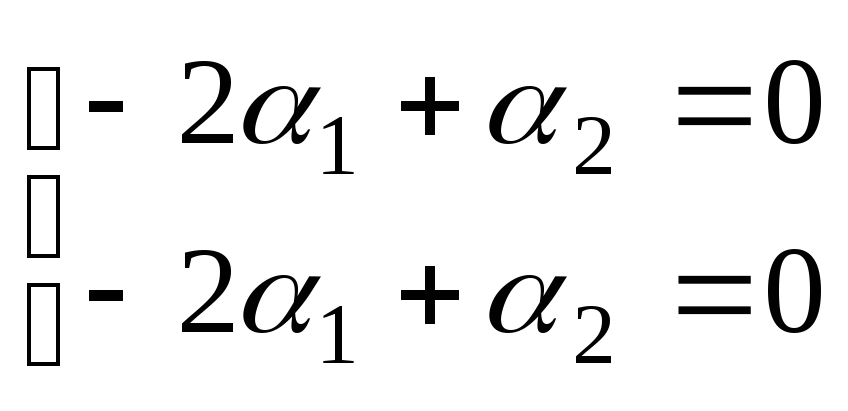
. Пусть , тогда

. Следовательно ,

Ответ:

18. Проинтегрировать систему уравнений матричным методом

Данная система равносильна матричному уравнению

, где ,.

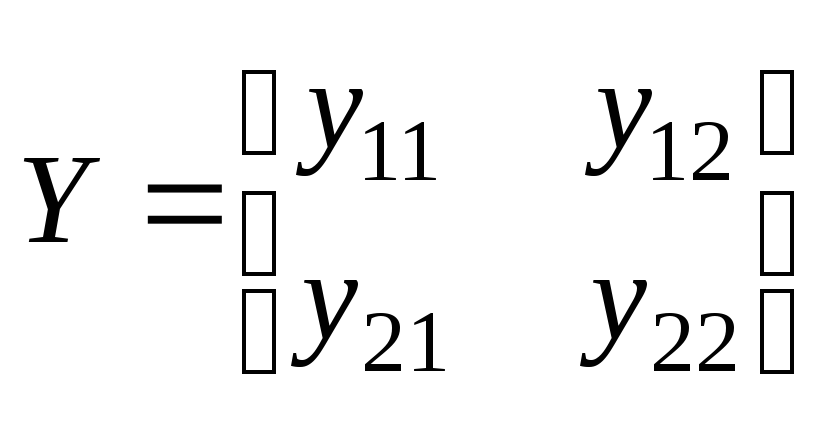Приведем матрицу А к каноническому виду; составим характеристическое уравнение

---