ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.04.2024
Просмотров: 111
Скачиваний: 1
СОДЕРЖАНИЕ
8 Вычислить определенный интеграл
9 Исследовать сходимость рядов
10 Исследовать ряды на сходимость
14 Вычислить криволинейный интеграл
26. Решить первую краевую задачу для уравнения теплопроводности:
28.Найти изолированные особые точки аналитической функции и выяснить их характер:
30. Решить интегральное уравнение
Решение:
![]()
В круге единичного радиуса, тогда
![]() - частное решение,
удовлетв ур-ю Пуассона.
- частное решение,
удовлетв ур-ю Пуассона.
![]()
Искомое решение будет иметь вид:
![]() -
оно записано в полярных координатах.
Где
-
оно записано в полярных координатах.
Где
![]() является решением уравнения Лапласа:
является решением уравнения Лапласа:

Рассмотрим
![]() в
полярных координатах:
в
полярных координатах:
![]()
Подставляем в
![]() и получим
и получим
![]()
Так как по условию r=1, то
![]()
![]()
По принципу максимума
![]() ,
,
тогда
![]() =
=![]()
и решение задачи
имеет вид
![]()
24. Решить задачу Дирихле для единичного круга, если на его границе задана функция:
А)
![]() ,
Б)
,
Б)![]() .
.
Решение:
А) ***теория***Рассмотри
уравнение Лапласа
![]() в полярных координатах
в полярных координатах![]() или то же самое
или то же самое![]() с граничными условиями
с граничными условиями![]() .
Решение этого уравнения имеем в виде
.
Решение этого уравнения имеем в виде
![]() .
Подставив вего в уравнение Лапласа в
полярных координатх, получи:
.
Подставив вего в уравнение Лапласа в
полярных координатх, получи:
![]() ю
Разделим переменные
ю
Разделим переменные
![]()
Перенесем лямда и приведем к общему знаменателю, тогда решение можно будет искать отдельно по двум уравнениям
1)
![]() и его решение есть
и его решение есть![]()
2)
![]() ,
его решение ищем в виде
,
его решение ищем в виде![]() ,
что дает
,
что дает
![]() ,
тогда
,
тогда
![]() .
.
Итак, решение задачи Дирихле имеет вид:
![]() ***
***
Для нашей задачи
![]() ,
то есть
,
то есть
![]()
![]()
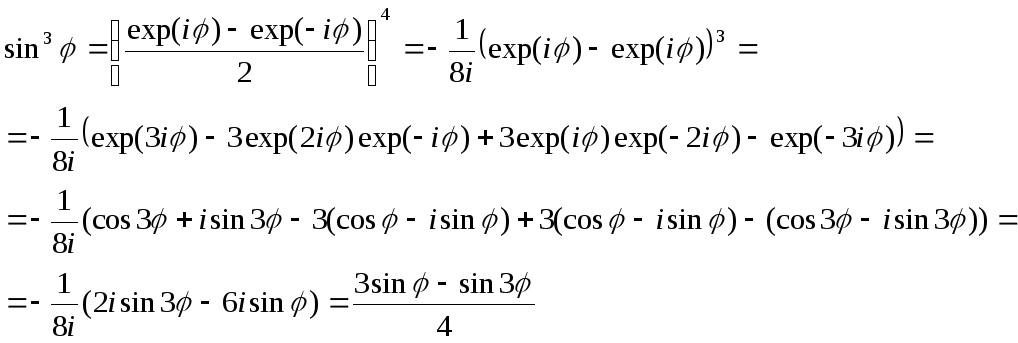
Следовательно решение примет вид
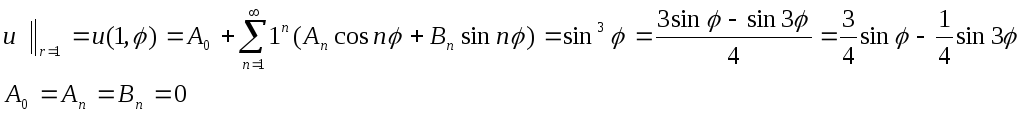
Б)
![]() .
.
Аналогично с первым решаем второе
![]()
![]() ****
****![]() ;
;![]() ****
****

25. Решить задачу Коши
![]()
Решение: преобразуем это уравнение к каноническому виду:
Уравнение характеристик
![]()
Распадается на 2 уравнения
![]()
интегралами которых являются прямые
![]()
Вводя новые переменные
![]()
Уравнение колебаний струны преобразуем к виду
![]()
Где
![]() -
функция только переменного
-
функция только переменного![]() .
Интегрируя (2) по
.
Интегрируя (2) по![]() при
фиксированном
при
фиксированном![]() ,
получим
,
получим
![]()
26. Решить первую краевую задачу для уравнения теплопроводности:
![]()
Решение:
Решение будем искать в виде
![]() (4), где Х(х)- функция
только первого х, T(t)-
функция только t.
(4), где Х(х)- функция
только первого х, T(t)-
функция только t.
Подставляя (4) в (1) и производя деление обеих частей равенства на XT, получим
![]() ,
где
,
где
![]() ,
так как левая часть равенства зависит
только отt
, а правая- только от х.
,
так как левая часть равенства зависит
только отt
, а правая- только от х.
Отсюда следует,
что
![]()
Граничные условия
(3) дают
![]()
Таким образом для
определения функции
![]() мы получи задачу о собственных значениях
(задача Штурма-Ляувиля)
мы получи задачу о собственных значениях
(задача Штурма-Ляувиля)
![]()
Только для значений
параметра
![]() ,
равных
,
равных![]() существуют нетривиальные решения
уравнения (5), равные
существуют нетривиальные решения
уравнения (5), равные
![]()
Этим значениям
![]() соответствуют решения уравнения (6)
соответствуют решения уравнения (6)
![]() где
где
![]() -
неопределенные пока коэффициенты.
-
неопределенные пока коэффициенты.
Таким образом
функции
![]() является частными уравнениями (1),
удовлетворяющими нулевым граничным
условием.
является частными уравнениями (1),
удовлетворяющими нулевым граничным
условием.
Требуя выполнения начальных условий, получаем
![]()
То есть С_п
являются коэффициентами Фурье функции
![]() при разложении её в ряд по синусам на
интервале (0,1)
при разложении её в ряд по синусам на
интервале (0,1)
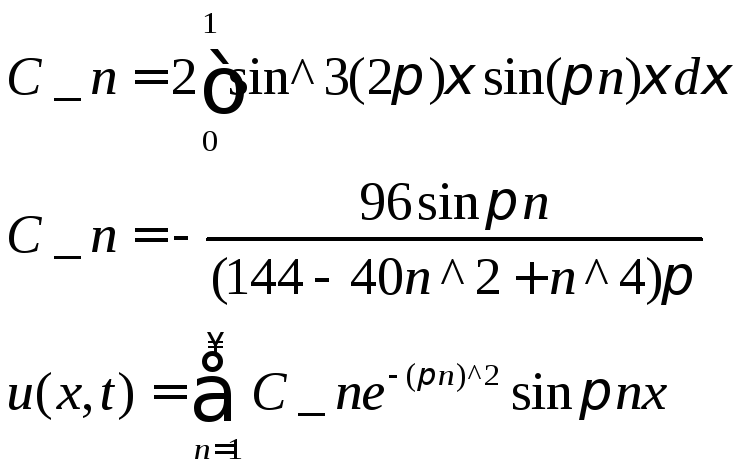
Таким образом искомое решение
![]()
27 разложить в ряд Лорана ф-ию 1/((z-2)(z-3)) в кольце 2<|z|3
Решение
Особые точки являются полюсами z=2, z=3
Разложим на простые дроби
![]()
![]()
![]()

28.Найти изолированные особые точки аналитической функции и выяснить их характер:
А)
![]() ,
Б)
,
Б)![]() ,
В)
,
В)![]() .
.
Решение:
А)
![]()
Особые точки
![]()
Очевидно, все точки изолированные и являются полюсами, так как
![]()
Б)
![]()
Запишем разложение в окрестностях особых точек.
Разложим дробь на элемент дроби
![]()
z=0: Первая дробь представляет собой слагаемое требуемого вида
![]() -
это разложение содержит только главную
часть, состоящую из одного числа; это
разложение имеет место в области
-
это разложение содержит только главную
часть, состоящую из одного числа; это
разложение имеет место в области
![]() .
Для второй дроби точкаz=0
не является особой, то получаем ряд
Тейлора в круге
.
Для второй дроби точкаz=0
не является особой, то получаем ряд
Тейлора в круге
![]() :
:
![]() .
Таким образом разложение
.
Таким образом разложение
![]() содержит конечное число отриц степенейz
(т=1)
следовательно точка z=0-
полюс первого
порядка.
содержит конечное число отриц степенейz
(т=1)
следовательно точка z=0-
полюс первого
порядка.
Аналогично
z=1:
![]() -
это разложение справедливо во всей
плоскости с выколотой точкой
-
это разложение справедливо во всей
плоскости с выколотой точкой
![]() ,
то есть в области
,
то есть в области![]() .
От первого слагаемого получим
.
От первого слагаемого получим
![]()
Таким образом
![]()
Как видим разложение содержит конечное число отриц степеней (1-z), следовательно точка z=1- полюс функции f(z), так как т=1, то полюс простой.
В)
![]()
Особая точка z=0
Разложение f(z) в ряд Лорана по степеням z :
![]()