Файл: Матан(Блок 1).doc

Уравнение Фредгольма с вырожденным ядром выглядит так: ,

λ-параметр.

12. Вероятностное пространство. Случайные величины. Закон больших чисел в форме Чебышева.

Опр. Набор трёх объектов , где -произвольное непустое множество, -алгебра подмножеств , - мера на и , наз. Вероятностным пространством.

Пусть дано вероятностное пространство и под случайной величиной понимаем некоторую функцию.

Опр. Числовая функция от элементарного события называется случайной величиной, если для любого числа x справедливо: .

Смысл определения: т.к. не любое подмножество является событием и все события составляют -алгебру подмножеств , то естественно рассмотреть такие , для которых имеет смысл говорить о вероятности попадания в достаточно простые числовые множества .

Известно, что нельзя заранее предвидеть, какие из возможных значений примет случайная величина в результате испытания, но при некоторых широких условиях суммарное поведение достаточно большого числа случ. Величин утрачивает случайный характер и становится закономерным. Эти условия указывают в теоремах под общим названием закон больших чисел.

---

Теорема ( нер-во Чебышева). Для любого >0 имеют место неравенства:

и .

Теорема (Чебышева). Если последовательно независимые случ. Величины и существует и для любого справедливо .

---

В.13. Задача Коши для уравнения колебания струны. Формула Даламбера.

Первая краевая задача для уравнения :

Найти функцию , определенную в области , , удовлетворяющую уравнению для , , граничным и начальным условиям

Если рассматривается явление в течении малого промежутка времени, когда влияние границ ещё не существенно, то вместо полной задачи можно рассматривать предельную задачу с начальными условиями для неограниченной области:

найти решение уравнения

для , , с начальными условиями

при (1)

Эту задачу называют задачей Коши.

Рассмотрим задачу для неограниченной струны:

(2)

(3)

Преобразуем уравнение (2) к каноническому виду

Уравнение характеристик , распадается на два уравнения:

, интегралами которых являются прямые

---

Вводя новые переменные ,уравнение колебаний струны преобразуется к виду: (4).

Найдем общий интеграл последнего уравнения. Очевидно, для всякого решения уравнения (4) , где - некоторая функция только переменной . Интегрируя это равенство по при фиксированном , получим:

, (5) где и являются функциями только переменных и . Т.к. всякое решение уравнения (4) м.б. представлено в виде (5) при соответствующем выборе и , то формула (3) является общим интегралом этого уравнения. Сл., функция (6) является общим интегралом уравнения (2).

Допустим, что решение рассматриваемой задачи существует, тогда оно даётся формулой (6). Определим функции и т.о., чтобы удовлетворялись начальные условия:

Интегрируя второе равенство получим:

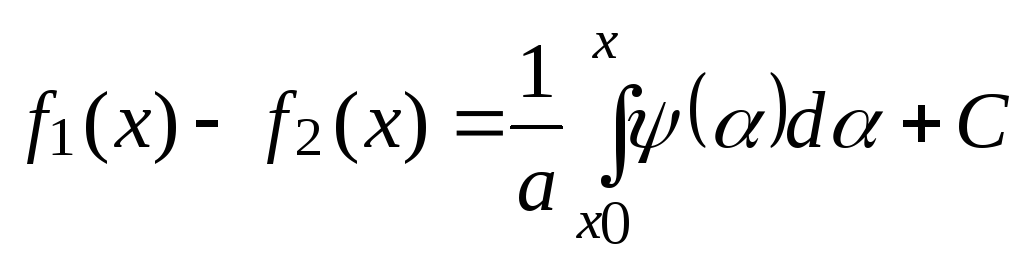,где и C – постоянные. Из равенств

находим

---

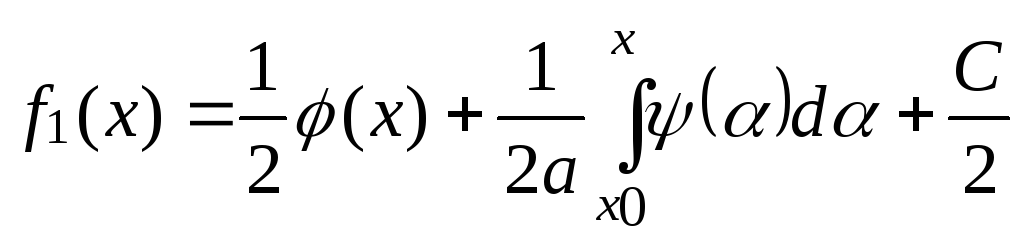
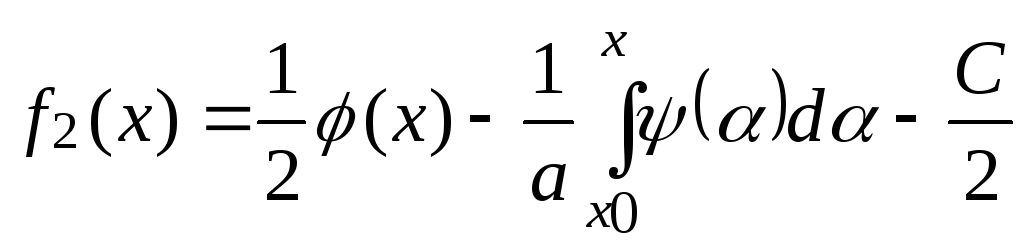(7)

Т.о. мы определили функции и ч/з заданные функции и , причем равенства (7) должны иметь место для любого значения аргумента. Подставляя в (6) найденные значения и , получим:

- формула Даламбера.

В.14. Постановка краевых задач для уравнения теплопроводности. Метод разделения переменных для решения первой краевой задачи.

Рассмотрим однородный стержень длины , теплоизолированный с боков и Д. тонкой, чтобы в любой момент времени температуру во всех точках поперечного сечения м.б. считать одинаковой. Процесс распространения температуры в стержне м.б. описан функцией имеет вид - уравнение теплопроводности, где - плотность теплового потока, равная количеству тепла, протекшего в единицу времени ч/з площадь в/см^2, c –удельная теплоемкость, - плотность. - плотность тепловых источников в точке х в момент t. В частности, если стержень однороден, то уравнение теплопроводности: , если источники отсутствуют, т.е. =0, то уравнение теплопроводности

1) Постановка краевых задач.

Для выделения единого решения уравнения теплопроводности Н. к уравнению присоединить начальные и граничные условия. Начальное условие состоит в задании значений функции в начальный момент .

---