Файл: Матан(Блок 1).doc

Рассмотрим 3 основных типа граничных условий.

1)На конце стержня x=0 задана температура , где - функция, заданная в некоторых промежутке , T – промежуток времени, в течении которого изучается процесс.

2) На конце , задано значение производной .

3) На конце задано линейное соотношение м/ду производной и функцией.

, где - коэффициент теплообмена, - некоторая функция.

Первая краевая задача состоит в отыскании решения уравнения теплопроводности при , удовлетворяющего условиям:

, где и - заданные функции.

Аналогично ставятся и другие краевые задачи с различными комбинациями краевых условий при x=0 и .

Первая краевая задача для полубесконечного стержня.

Найти решение уравнения теплопроводности в области и , удовлетворяющее условиям

2) Метод разделения переменных.

Рассмотрим первую краевую задачу для уравнения теплопроводности на отрезке: (1) с начальными условиями (2) и граничными условиями (3)

Для решения этой задачи рассматривают, как принято в методе разделения переменных, сначала основную вспомогательную задачу:

Найти решение уравнения , не равное тождественно нулю, удовлетворяющее однородным граничным условиям(3`) и представимое в виде , (4) где - функция только переменного x, - функция только переменного t.

Подставляя (4) в (1) и производя деление обеих частей равенства на , получим:

, т.к. левая часть зависит только от t, правая - от х.

,(5) (5`)

Граничные условия (3`) дают:

Т.о. для определения функции X(x) получим задачу о собственных значен. (Штурма - Лиувилля) ,(6)

Известно, что только для значений параметра , равных (7) существует нетривиальное решение уравнения (5), равные (8)

Этим значениям соответствуют решения уравнения (5`)

(9)

Функции (10) является частными решениями уравнения (1), удовлетворяющими нулевым граничным условиям

Составим ряд (*)

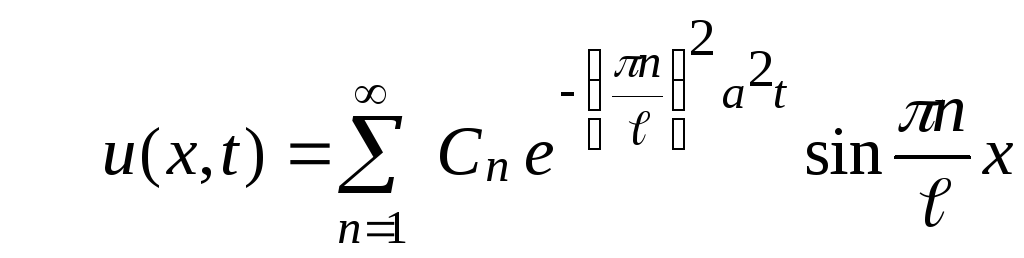Функция удовлетворяет граничным условиям, т.к. им удовлетворяют все члены ряда. Требуя выполнения начальных условий, получаем:

(11), т.е. является коэффициентами Фурье функции при разложении её в ряд по синусам на интервале :

(12)

Т.о., ряд (*) с коэффициентами , определенными по формуле (12) удовлетворяет всем условиям искомой задачи и является решением задач (1),(2),(3).