Файл: Матан(Блок 1).doc

Т. Если ряд (5) сх-ся не при всех значениях z и не только при z=0, то существует число R>0 такое, что ряд сходится абсолютно при и расходится при

В.9. Ряд Фурье по ортогональной системе функций. Неравенство Бесселя, равенство Парсеваля, сходимость ряда Фурье.

Опр.: Пусть дана посл-ть, элементами кот-й явл-ся ф-ции (1) и определены в некоторой области . Такая посл-ть называется функциональной.

Опр.: Функциональный ряд вида (2) наз-ся тригонометрическим рядом.

Каждый член тригонометрического ряда – это ф-ция с периодом . Поэтому, если ряд (2) будет сходится, то его сумма будет периодическая с периодом .

Опр. Система функций называется ортогональной ситемой на , если выполняются 2 условия:

1) 2)

Т. Система функций является ортогональной системой на промежутке .

Любой бесконечно дифференцируемой функции соответствует ряд Тейлора.

Возьмём функцию , определённую на и сотавим с её помощью числа 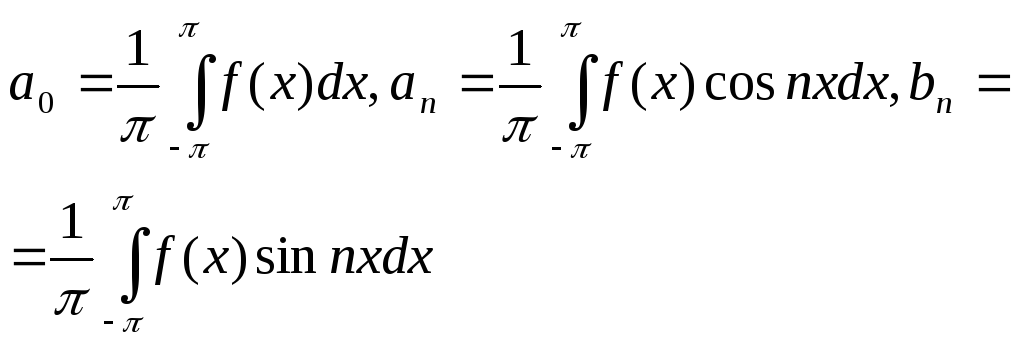(3)

Опр. Тригонометрический ряд, коэффициентами кот. служат числа (3) наз-ся рядом Фурье функции, а сами коэффициенты наз-ся коэф-ми Фурье функции .

---

Чтобы можно было вычислить коэф-ты Фурье, нужно предположить, чтобы функция была интегрируема на , след. каждой такой функции можно поставить в соответствие ряд Фурье. е

Утв. Если функциональный ряд сх-ся на и некоторая ограниченная на функция, то ряд также будет равномерно сходится на .

Т. Если функция разлагается на в равномерно сходящийся тригонометрический ряд есть её ряд Фурье.

Ряд Фурье четной и нечетной функции.

Пусть функция определена на и является четной: . Тогда её коэффициенты Фурье , .

Пусть определенная на - нечетная, т.е. . Тогда, , .

Сходимость ряда Фурье.

Будем говорить , что функция , определённая на всей числовой прямой и периодическая с периодом , является периодическим продолжением функции ; если на . Если на ряд Фурье сх-ся к функции , то он сх-ся на всей числовой прямой к её периодическому продолжению.

---

Т.Пусть функция и её производная - непрерывные функции на или же имеют на нём конечное число точек разрыва 1-го рода. Тогда ряд Фурье функции сх-ся на всей числовой прямой, причем в каждой точке , в которой непрерывна, сумма ряда равна , а в каждой точке разрыва функции сумма ряда равна , где и . На концах отрезка сумма равна . В любой точке сумма ряда Фурье равна , если x – точка непрерывности , и равна , если x – точка разрыва , где - периодическое продолжение функции .

---

Ряд Фурье с периодом .

Пусть определена на и удовлетворяет на отрезке . Разложим её в ряд Фурье. Положим и рассмотрим функцию . Разложим на в ряд Фурье: , где .

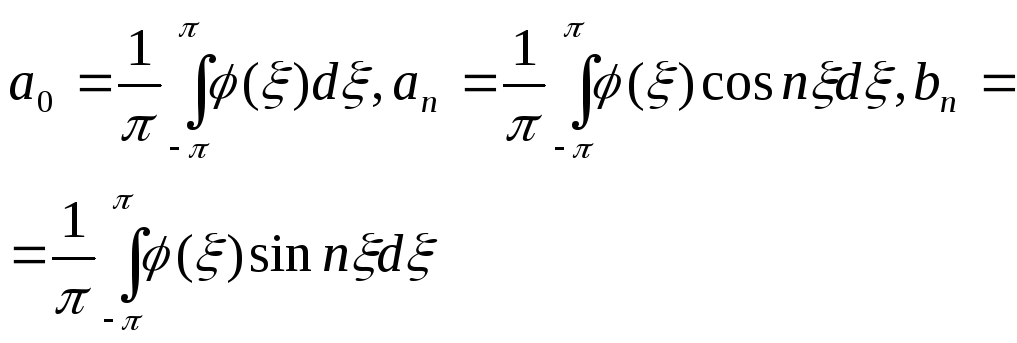П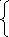ерейдем к примеру (4)примет вид:

,

.

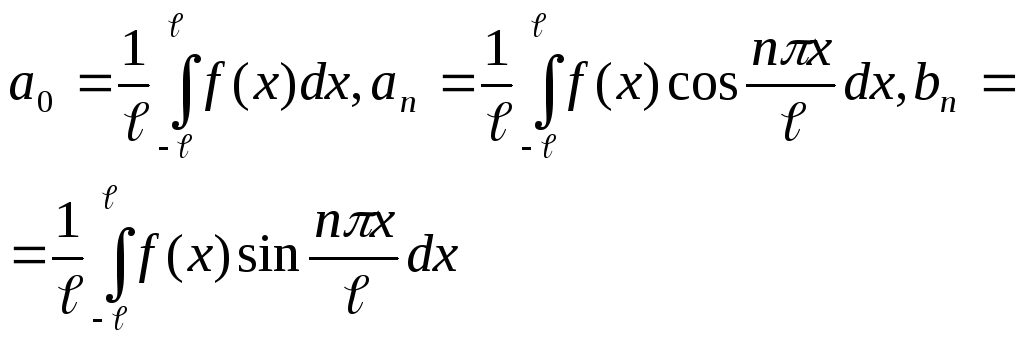№10. Линейные обыкновенные дифференциальные уравнения и их системы. Фундаментальная система решений. Определитель Вронского.

Опр1 Обыкновенным диф-ым уравн-м называется рав-во, содержащее независимую переменную х, независимую функцию у и ее производные у′,у′′,…,у⁽ⁿ⁾: F(x,y, у′,у′′,…,у⁽ⁿ⁾)=0 (1), F, если не оговорено предполагают действительной функцией.

Опр2. Диф-ое уравн-ие 1го порядка называется линейным, если его можно записать в виде у′+p(x)y=g(x),где p(x) и g(x) заданные функции, в частности постоянные. Линейным диф-м ур-м 2го порядка назыв-ся уравнение вида a(x) у′′+b(x) у′+c(x)y=f(x), где a(x)≠0,b(x),c(x),f(x)функции непрерывные на инт (а,b).Уравнение вида у⁽ⁿ⁾+a_n-1y^(n-1)+a₁y′+a₀y=0, где a_0, a_1,…, a_n-1=const(числа ≠0) назыв-ся линейным однородным уравнением n-го порядка.

Опр3 Пусть у₁=у₁(х),у₂=у₂(х) два каких-либо частных решения однородного диф-го уравн-я 2го порядка. Определитель вида W(x)=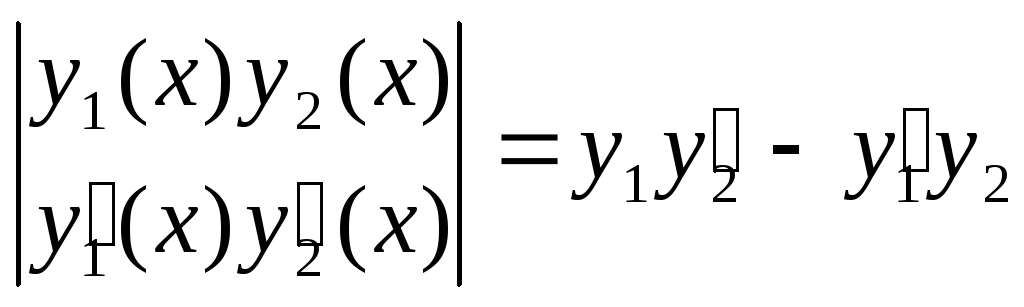 наз-ся определителем Вронского или вронскианом для у₁ и у_2.

---

Если опред-ль Вронского в точке х₀=0, то он =0 на всем интерв (a,b).Если опред Вронск в точке х₀≠0, то он ≠0 ни в одной точке инт-ла (a,b).

Опр4 Система частных решений у₁=у₁(х),у₂=у₂(х) однородного диф-го уравн-я 2го порядка наз-ся фундаментальной системой решения этого уравнения,если W(x) ≠0 на (a,b).

Опр5 Системой дифференциальных уравнений наз-ся система вида:

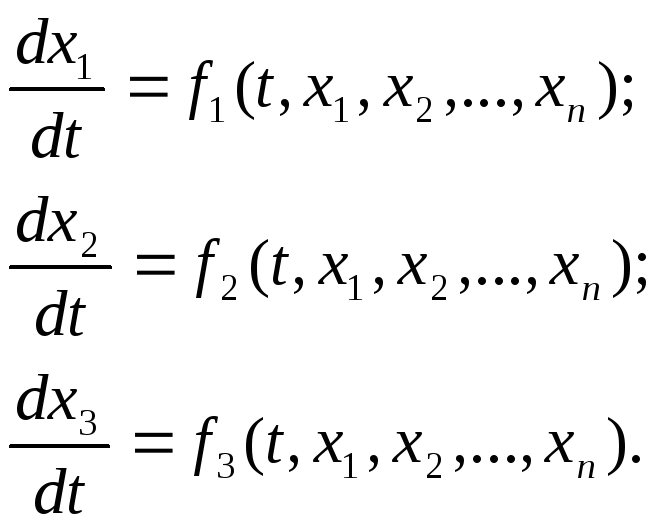
Опр6Система вида ==…=

наз-ся системой диф-ых ур-й в симметричной форме(?).

Опр7 Система диф-ых ур-й наз-ся линейной,если она линейна относительно неизвестных функций и их производных. Система n-линейных ур-ий 1го порядка, записанная в: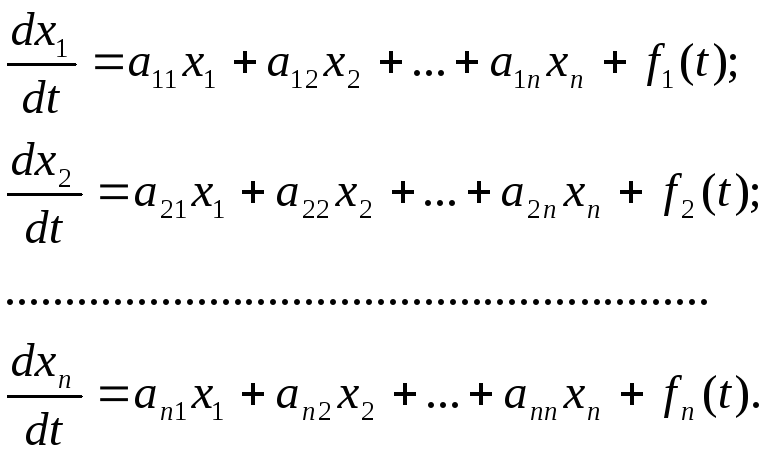или в матричной векторной форме

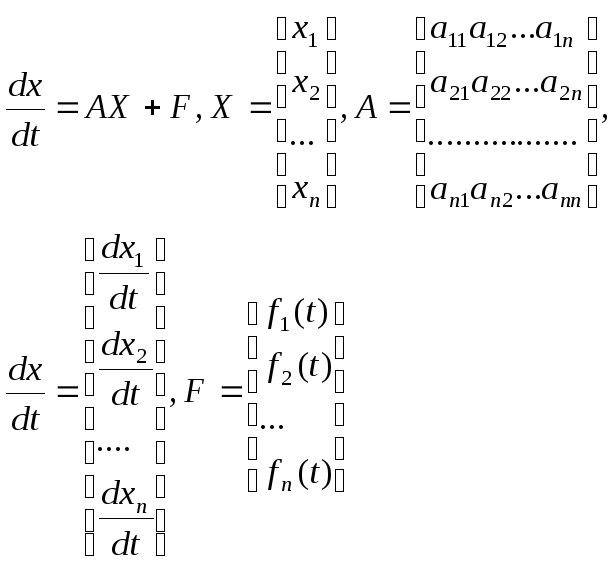
Опр8 Система n линейно независимых решений системы наз-ся ее фундаментальной системой решений,здесь A=A(t)-квадратная матрица разм. nn,элементы кот a_ij(t),ij=1,2,…,n непрерывные функции на I.

№11 Опр1 Интегр-м уравн-м наз-т ур-ие,которое сод-т некотор искомую функцию под знаком интегр.

Опр2 Ур-ие вида K(t,τ)y(τ)dτ+f(t), где y(t)-искомая функция,а f(t)- задан на интерв (a,b) функция наз-ся ур-ем Фредгольма 2го рода. Уравнение вида K(t,τ)y(τ)dτ=f(t) наз-ся ур-ем Фредгольма 1го рода, где K(t,τ)-ядро этих интегр-х уравнений, f(t)-свободный член.

Опр3 Ядро интегр-го ур-ия K(t,τ),которое можно представить в виде

K(t,τ)= наз-ся вырожденным ядром.

---