Файл: Тема 10.doc

Прологарифмировав функцию Гомперца , получим модифицированную экспоненту. Вводя в модифицированную экспоненту величину, обратную, получим логистическую кривую. Следовательно, логистическая кривая имеет сходство с кривой Гомперца. Различие между ними состоит в том, что изменение во времени первых разностей кривой Гомперца асимметрично, а у логистической кривой их изменение во времени имеет симметричный вид, напоминающий нормальное распределение.

Для выбора уравнения можно воспользоваться формулой стандартной ошибки

Можно также применить критерий наименьшей суммы квадра­тов отклонения эмпирических уровней от теоретических

.

Из множества возможных уравнений тренда можно выбрать то уравнение, которому соответствует минимальное значение, т.е. критерий наименьших квадратов отклонений, либо использовать формулу средней ошибки аппроксимации:

Все эти характеристики имеют один и тот же смысл: показывают, как близко аналитическая функция выравнивания огибает все значения исходного ряда. Поэтому, проводя сравнительную оценку моделей тренда, можно использовать лишь одну из перечисленных характеристик. Результаты такой оценки, полученные на основе прочих характеристик, как правило, совпадают. Наиболее часто в качестве меры точности аппроксимации выбирают остаточную дисперсию или остаточное среднее квадратическое отклонение.

Расчет параметров полиномов различными методами. После того как выяснен характер кривой развития, необходимо определить ее параметры. Элементарный метод определения параметров уравнения тренда, описанного полиномом или экспонентой, состоит в решении системы уравненийпо известным уровням ряда динамики.

Пример. Дан ряд динамики, представленный табл. 10.2. Приняв условные обозначения времени через и взяв две точки - конечный и начальный уровни, можно построитьуравнение прямой по этим двум точкам.

Уравнение прямой имеет вид: 1996 г. его уровень составил:; Для 2001 г.:.

Решая эти уравнения как систему уравнений, получим: ;;. Следовательно, приближенная модель динамики готовой продукции выражается уравнением. Здесь параметр соответствует абсолютному приросту.

Можно предположить и развитие по параболе второго порядка: , но тогда следует взять три точки, например 1996, 1999, 2001 гг., т.е. уровни при,,.

Составим систему трех уравнений с тремя неизвестными:

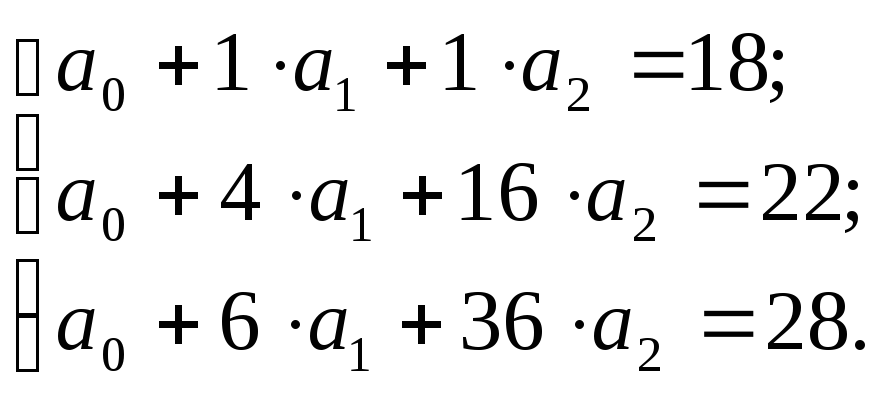
Решая эту систему, получим: ,и, а само уравнение применительно к нашему примеру выразится, что в приближенной форме определит модель динамики данного явления.

Отрицательным моментом в таком моделировании тренда служат разные числовые выражения параметров в различных точках их определения.

Другим способом определения параметров уравнения является метод средних значений (линейных отклонений), заключающийся в следующем: ряд расчленяется на две примерно равные части и вводится требование, чтобы сумма выравненных значений в каждой части совпала с суммой фактических значений, т.е. чтобы сумма отклонений фактических данных от выравненных равнялась нулю.

В случае выравнивания по прямой линии

получим:

откуда

.

Если применить это требование к каждой из двух частей ряда, то, вычислив для каждой части динамического ряда и, получим два уравнения с двумя неизвестными. В результате решения этой системы уравнений находим параметры и, т.е. начальный уровень и скорость ряда. При этом значение.

Метод средних значений прост и требует минимального количества вычислений. Его недостаток заключается в том, что при произвольном расчленении ряда на две части мы будем получать разные результаты. Метод средних значений, как и выравнивание ряда динамики с помощью среднего прироста и темпа роста, может применяться для ориентировочных расчетов.

Выравнивание ряда динамики с помощью метода конечных разностей. Этот метод заключается в следующем.

Пусть ряд динамики описывается полиномом-й степени. Для полинома-й степени вычислим первые разности:

;

вторые разности:

и т.д.

Общая формула -й разности:

Любой член () ряда динамики можно выразить через начальный уровень рядаи конечные разности:

,

но , поэтому и т.д.

Отсюда получаем:

Если первые разности не равны, но варьируют с незначительными отклонениями друг от друга, а средняя арифметическая вторых разностей настолько мала, что ею можно пренебречь, то первые разности можно считать практически равными.

Окончательная формула для расчета уровней ряда динамики при равных или почти равных первых разностях будет:

Если, анализируя вторые разности, мы придем к выводу, что они практически равны, то, вычислив коэффициенты параболы 2-го порядка, получим тренд ряда динамики:

Метод наименьших квадратов при расчете параметров полиномов. Этот метод при моделировании рядов динамики можно рассматривать как некоторый прием получения оценки детерминированной компоненты, которая характеризует тренд изучаемого явления.

В экономике часто применяется функция вида: