Файл: Тема 9.doc

Регрессионный метод заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной) и многофакторной (множественной).

По форме зависимости различают:

линейную регрессию, которая выражается уравнением прямой (линейной функцией) вида: ;
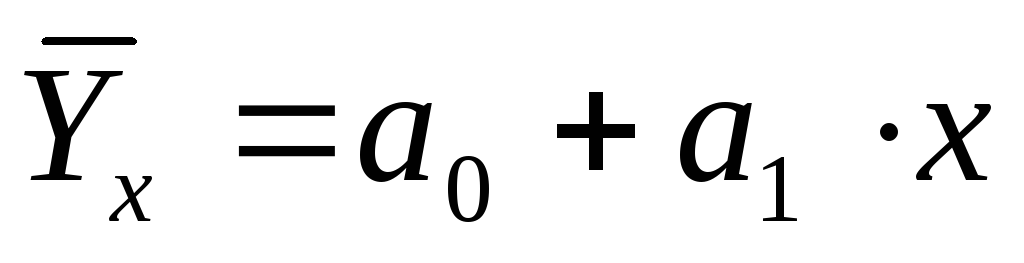нелинейную регрессию, которая выражается уравнениями вида:

- парабола;

- гипербола и т.д.

По направлению связи различают:

прямую регрессию (положительную), возникающую при условии, если с увеличением или уменьшением независимой величины значения зависимой также соответственно увеличиваются или уменьшаются;
обратную (отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.

Положительную и отрицательную регрессии можно легче понять, если использовать их графическое изображение (рис. 9.2, 9.3).

Для простой (парной) регрессии в условиях, когда достаточно полно установлены причинно-следственные связи, приобретает практический смысл только последнее положение; при множественности причинных связей невозможно четко отграничить одни причинные явления от других.

9.2 Основные задачи и предпосылки применения корреляционно-регрессионного анализа

Все явления и процессы, характеризующие социально-экономическое развитие и составляющие единую систему национальных счетов, тесно взаимосвязаны и взаимозависимы между собой.

В статистике показатели, характеризующие эти явления, могут быть связаны либо корреляционной зависимостью, либо быть независимыми (см. табл. 9.1).

Корреляционная зависимость является частным случаем стохастической зависимости, при которой изменение значений факторных признаков влечет за собой изменение среднего значения результативного признака.

Корреляционная зависимость исследуется с помощью методов корреляционного и регрессионного анализов.

Корреляционный анализ изучает взаимосвязи показателей и позволяет оценить:

тесноту связи между показателями с помощью парных, частных и множественных коэффициентов корреляции;
уравнение регрессии.

Основной предпосылкой применения корреляционного анализа является необходимость подчинения совокупности значений всех факторных и результативного () признаков-мерному нормальному закону распределения или близость к нему. Если объем исследуемой совокупности достаточно большой, то нормальность распределения может быть подтверждена на основе расчета и анализа критериев Пирсона, Ястремского, Боярского, Колмогорова, чисел Вастергарда и т.д. Если, то закон распределения исходных данных определяется на базе построения и визуального анализа поля корреляции. При этом если в расположении точек наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному распределению.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака () от факторных.

Основной предпосылкой регрессионного анализа является то, что только результативный признак () подчиняется нормальному закону распределения, а факторные признаки могут иметь произвольный закон распределения. В анализе динамических рядов в качестве факторного признака выступает время. При этом в регрессионном анализе заранее подразумевается наличие причинно-следственных связей между результативным () и факторными признаками.

Уравнение регрессии, или статистическая модель связи социально-экономических явлений, выражаемая функцией

является достаточно адекватной реальному моделируемому явлению или процессу, если выполняются следующие требования к их построению:

совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями;
моделируемые явления должны описываться одним или несколькими уравнениями причинно-следственных связей;
все факторные признаки должны иметь количественное (цифровое) выражение;
объем исследуемой выборочной совокупности должен быть достаточно большим;
причинно-следственные связи между явлениями и процессами должны описываться линейной или приводимой к линейной формами зависимости;
параметры модели связи не должны иметь количественных ограничений;
территориальная и временная структура изучаемой совокупности должна быть постоянной.

Соблюдение данных требований позволяет исследователю построить статистическую модель связи, наилучшим образом аппроксимирующую моделируемые социально-экономические явления и процессы.

Теоретическая обоснованность моделей взаимосвязи, построенных на основе корреляционно-регрессионного анализа, обеспечивается соблюдением следующих основных условий.

все признаки и их совместные распределения должны подчиняться нормальному закону распределения;
дисперсия моделируемого признака () должна все время оставаться постоянной при изменении величины () и значений факторных признаков;
отдельные наблюдения должны быть независимыми, т.е. результаты, полученные в 1-м наблюдении, не должны быть связаны с предыдущими и содержать информацию о последующих наблюдениях, а также влиять на них.

Отступление от выполнения этих условий и предпосылок приводит к тому, что модель регрессии будет неадекватно отражать реально существующие связи между анализируемыми признаками.

Одной из проблем построения уравнения регрессии является ее размерность, т.е. определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным.

Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, реализуемую быстрее и качественнее. В то же время построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс в единой системе национального счетоводства.

Практика выработала определенный критерий, позволяющий установить оптимальное соотношение между числом факторных признаков, включаемых в модель, и объемом исследуемой совокупности. Согласно данному критерию, число факторных признаков () должно быть в 5-6 раз меньше объема изучаемой совокупности.

Общая блок-схема реализации корреляционного и регрессионного методов анализа представлена на рис. 9.4.

Приведенная последовательность реализации корреляционного и регрессионного методов анализа позволяет достаточно полно охарактеризовать и смоделировать реально существующие взаимосвязи и взаимозависимости между показателями, характеризующими развитие социально-экономических явлений и процессов.

Построение корреляционно-регрессионных моделей, какими бы сложными они ни были, само по себе не вскрывает полностью всех причинно-следственных связей. Основой их адекватности является предварительный качественный анализ, основанный на учете специфики и особенностей исследуемых социально-экономических явлений и процессов.

9.3 Парная регрессия на основе метода наименьших квадратов и метода группировок

Парная регрессия характеризует связь между двумя признаками - результативным и факторным. Аналитическая связь между ними описывается следующими уравнениями:

прямой	-	(9.1)
гиперболы	-
параболы	- и т.д.

Определить тип уравнения можно, исследуя зависимость графически. Однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи - гиперболическая. Если факторный признак увеличивается в арифметической прогрессии, а результативный - значительно быстрее, то используется связь параболическая или степенная.

Оценка параметров уравнений регрессии (,ив уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Основной принцип метода наименьших квадратов рассмотрим на следующем примере: будем считать, что две величины (два показателя)ивзаимосвязаны между собой, причемнаходится в некоторой зависимости от. Следовательно, будет зависимой,а -независимой величинами.