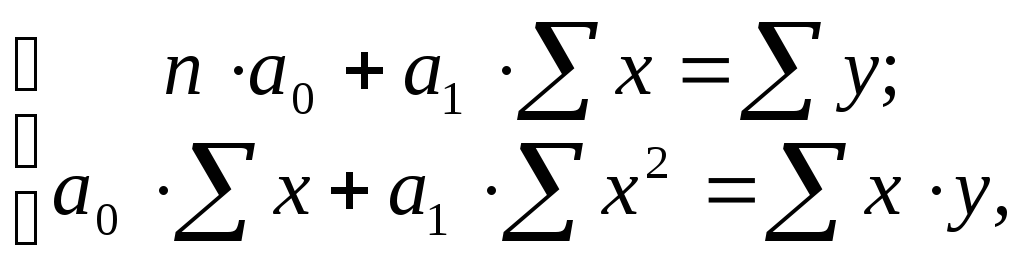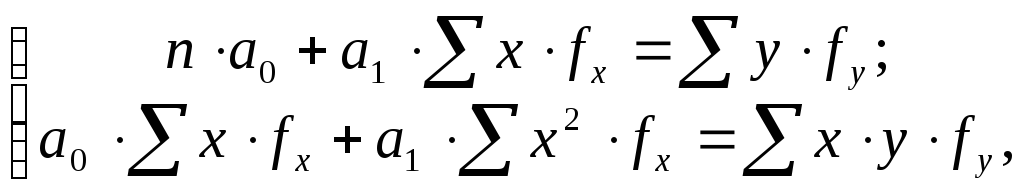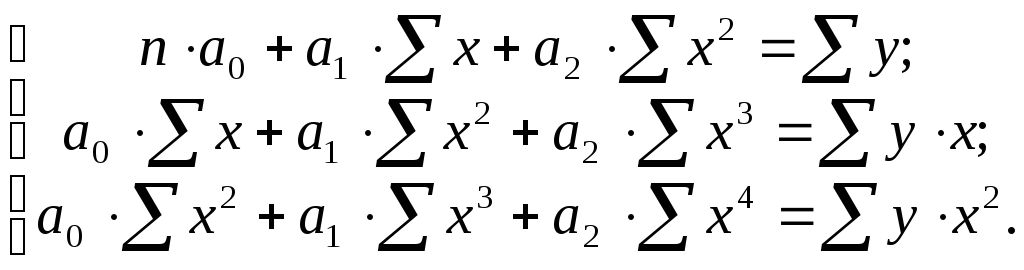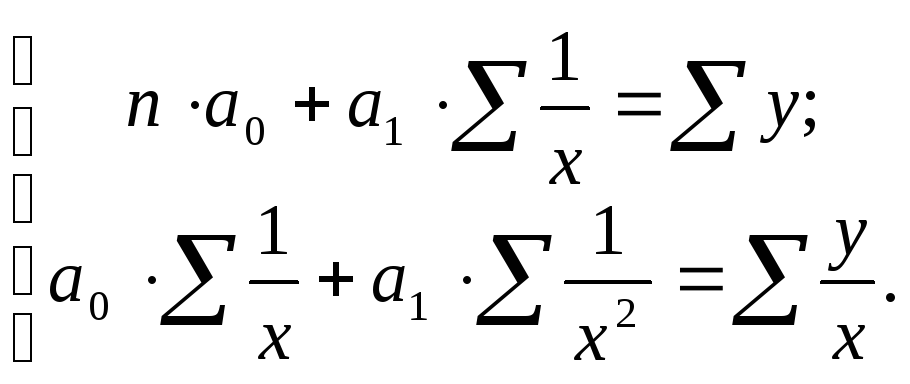Файл: Тема 9.doc

Сущность метода наименьших квадратов заключается в нахождении параметров модели (,), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:

.

Для прямой зависимости:

.

Рассмотрим в качестве функции параметров и, проведем математические преобразования (дифференцирование) и получим:

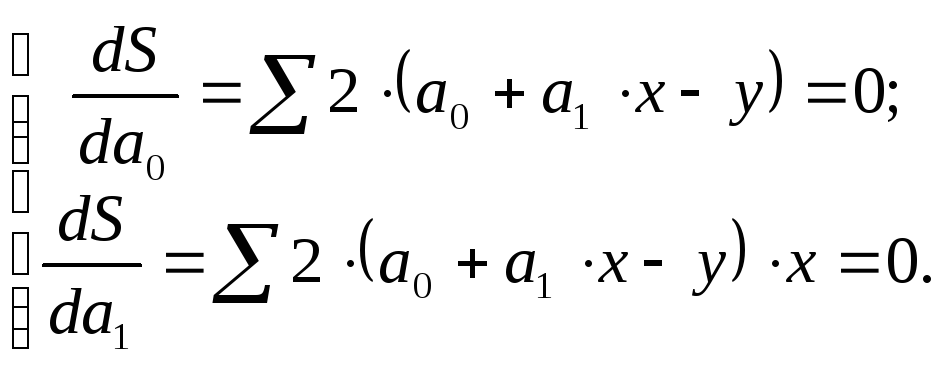
Откуда система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов примет следующий вид:

(9.2)

где - объем исследуемой совокупности (число единиц наблюдений).

В уравнениях регрессии параметр показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр(а в уравнении параболы и) - коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

На практике часто исследования проводятся по большому числу наблюдений. В этом случае исходные данные удобнее представлять в сводной корреляционной таблице. При этом анализу подвергаются сгруппированные данные и по факторному , и по результативному признакам, т.е. уравнение парной регрессии целесообразно строить на основесгруппированных данных.

---

Если значения признаков и заданы в определенных интервалах (а–b), то для каждого интервала сначала определяют середину интервала, а затем уже коррелируют значения и и строят 2 уравнения регрессии между ними.

Система нормальных уравнений для определения коэффициентов уравнения регрессии в данном случае примет вид:

(9.3)

где - объем рассматриваемой выборки;

; - частота попадания факторного (результативного) признака в определенный интервал;

; - значение результативного и факторного признаков по конкретной группе.

Если связь между признаками икриволинейная и описывается уравнением параболы второго порядка, то

.

В данном случае задача сводится к определению неизвестных параметров: ,,.

Значения величин и представлены двумя рядами данных:

---

Если бы все значения, полученные по данным наблюдения, лежали строго на кривой, описываемой уравнением параболы, или для каждой из точек было бы справедливо равенство:

,

то не существовало бы никаких проблем. Однако на практике имеем другое:

где - разность между данными наблюдения и данными, полученными по уравнению связи.

Эта разность как раз и появляется из-за ошибок упрощения, поэтому возникает проблема нахождения таких коэффициентов уравнения (регрессии), при которых ошибка была бы минимальной. Можно минимизировать сумму абсолютных отклонений (ошибок), т.е.

,

или минимизировать сумму кубических ошибок, и тогда получим метод наименьших кубов:

,

или, наконец, минимизировать наибольшую абсолютную ошибку:

.

Однако наиболее оптимальным вариантом является оценка ошибки по методу наименьших квадратов:

.

Метод наименьших квадратов обладает тем замечательным свойством, что делает число нормальных уравнений равным числу неизвестных коэффициентов. Приведенное уравнение параболы второго порядка имеет три неизвестных коэффициента: ,,.

Следовательно, применяя метод наименьших квадратов, мы получим уравнение:

.

Для нахождения значений неизвестных коэффициентов ,,, при которых функция была бы минимальной, необходимо приравнять частные производные по этим величинам нулю, т.е.

---

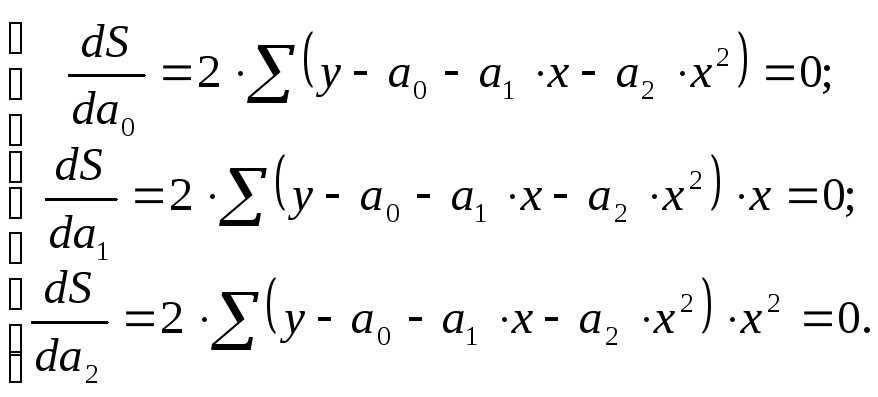
Проделав простейшие преобразования, получим систему нормальных уравнений:

(9.4)

Решив систему, найдем значения неизвестных коэффициентов ,,и получим уравнение регрессии. Вычислим по уравнению регрессии теоретические значения и сравним с данными наблюдения, т.е. рассчитаем так называемую остаточную сумму квадратов (табл. 9.2).

Таблица 9.2
Расчет остаточной суммы квадратов
Номер наблюдения	Значения по данным
	наблюдения	Уравнения регрессии
1
2
3
.

---

Остаточная сумма квадратов совпадает с минимальной возможной величиной по методу наименьших квадратов.

Оценка обратной зависимости между и, когда с увеличением (уменьшением) уменьшается (увеличивается) результативный признак, может быть осуществлена на основе уравнения гиперболы:

.

Систему нормальных уравнений для нахождения параметров гиперболы можно представить следующим образом:

(9.5)

Применение метода наименьших квадратов объясняется неизбежным наличием случайных ошибок в результатах опыта.

Статистические данные обладают ошибками упрощения, которые возникают как следствие:

• неполноты охвата, потому что часть единиц совокупности, полученных в результате наблюдения, не может быть использована в исследовании;

• неполноты факторов, определяющих то или иное социально-экономическое явление, в силу того, что ни в одно уравнение, или модель, нельзя включить бесконечное число аргументов (во всех случаях отбирается только часть воздействующих факторов, причем отбор носит чисто субъективный характер);

• характера выбранного уравнения связи. Как бы хорошо оно ни было обосновано, как бы теоретически адекватно ни описывало исследуемое явление, оно не может быть его точным аналогом.

Решение вопроса о возможности использования метода наименьших квадратов для изучения связей между социально-экономическими явлениями зависит от свойства оценок, получаемых с помощью этого метода.

Даже при сравнительно небольшом числе наблюдений применение метода наименьших квадратов позволяет получить достоверные оценки.

Метод наименьших квадратов может быть также использован в анализе косвенных наблюдений, являющихся функциями многих неизвестных.

Обобщенная блок-схема построения уравнения парной регрессии представлена на рис. 9.5.

---