Файл: Тема 9.doc

Наиболее сложным этапом, завершающим регрессионный анализ, является интерпретация уравнения, т.е. перевод его с языка статистики и математики на язык экономики.

Интерпретация моделей регрессии (рис. 9.7) осуществляется методами той отрасли знаний, к которой относятся исследуемые явления. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом иоценки значимости входящих в модель факторных признаков, т.е. с выяснения, как они влияют на величину результативного признака. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый. Особое значение при этом имеет знак перед коэффициентом регрессии. Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает; если факторный признак со знаком минус, то с его увеличением результативный признак уменьшается. Интерпретация этих знаков полностью определяется социально-экономическим содержанием моделируемого (результативного) признака. Если его величина изменяется в сторону увеличения, то плюсовые знаки факторных признаков имеют положительное влияние. При изменении результативного признака в сторону снижения положительное значение имеют минусовые знаки факторных признаков. Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он со знаком минус, то необходимо проверить расчеты параметров уравнения регрессии. Такое явление чаще всего бывает из-за допущенных ошибок при решении. Однако при анализе совокупного влияния факторов при наличии взаимосвязей между ними характер их влияния может меняться. Для того чтобы быть уверенным, что факторный признак изменил знак влияния, необходима тщательная проверка решения данной модели, так как часто знаки могут меняться в силу допущенных ошибок при сборе или обработке информации.

При анализе адекватности уравнения регрессии исследуемому процессу возможны следующие варианты.

построенная модель на основе ее проверки по 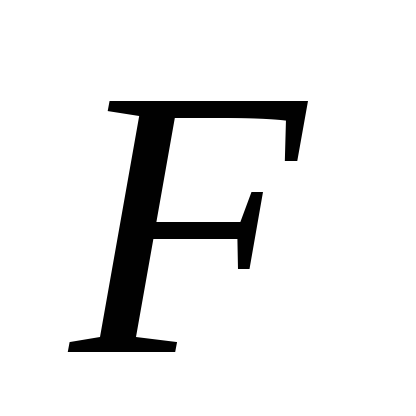-критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений и осуществления прогнозов;
модель по -критерию Фишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решений, но не для производства прогнозов;
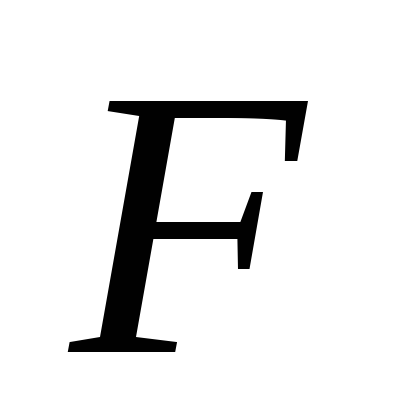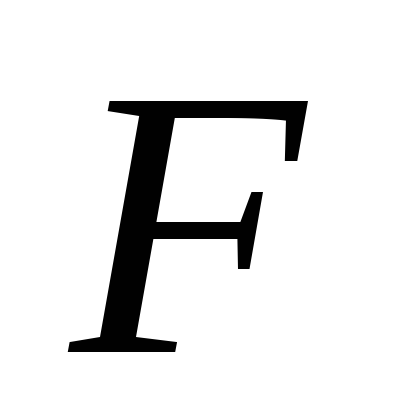модель по -критерию Фишера адекватна, но все коэффициенты регрессии незначимы. В этом случае модель полностью считается неадекватной. На ее основе не принимаются решения и не осуществляются прогнозы.

С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности, определяемые по формуле

(9.15)

где		коэффициент эластичности;
		среднее значение соответствующего факторного признака;
		среднее значение результативного признака;
		коэффициент регрессии при соответствующем факторном признаке.

Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%.

Другим показателем экономического анализа является частный коэффициент детерминации:

(9.16)

где		частный коэффициент детерминации:
		парный коэффициент корреляции между результативным и -м факторным признаками;
		соответствующий коэффициент уравнения множественной регрессии в стандартизованном масштабе.

Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией 1-го признака, входящего в множественное уравнение регрессии.

Множественный коэффициент детерминации () представляющий собой множественный коэффициент корреляции в квадрате; он характеризует, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель.

Для более точной оценки влияния каждого факторного признака на моделируемый используют -коэффициент, определяемый по формуле

(9.17)

где		коэффициент вариации соответствующего факторного признака;
		для фактора - численности работающих:

Таким образом, обобщенная блок-схема интерпретации моделей регрессии имеет вид (рис. 9.7).

Наиболее полная экономическая интерпретация моделей регрессии позволяет выявить резервы развития и повышения деловой активности субъектов экономики.

9.6 Собственно-корреляционные параметрические методы изучения связи. Оценка существенности корреляции

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторов.

Линейный коэффициент корреляции был впервые введен в начале 1890-х гг. Пирсоном, Эджвортом и Велдоном и характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

В теории разработаны и на практике применяются различные модификации формул для расчета данного коэффициента:

(9.18)

где

линейный коэффициент корреляции.

Используя математические свойства средней и формулу (9.18), получим:

(9.19)

Дальнейшие преобразования позволяют получить следующую формулу линейного коэффициента корреляции:

, или,

(9.20)

где

число наблюдений.

Произведя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:

(9.21)

или

(9.22)

Коэффициент корреляции может быть выражен через дисперсии слагаемых:

(9.23)

Формулы (9.21), (9.22), (9.23) применяются при изучении совокупностей малого объема ().

Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой

(9.24)

где		коэффициент регрессии в уравнении связи;
		среднее квадратическое отклонение соответствующего статистически существенного факторного признака.

Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределение которых близко к нормальному. Легко доказывается, что условие является необходимым и достаточным для того, чтобы величинык были независимы. При этом условии коэффициенты регрессии,также обращаются в нуль, а прямые регрессии по и по оказываются взаимно перпендикулярными (параллельными: одна оси абсцисс, а вторая оси ординат).
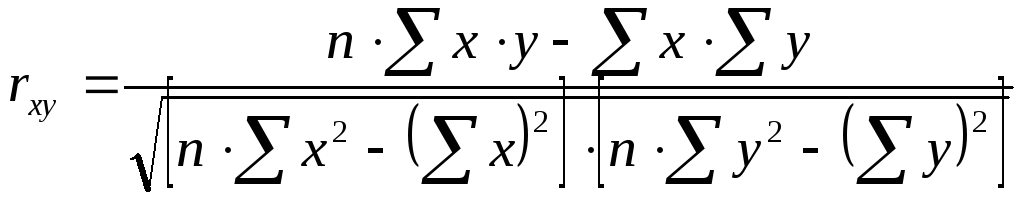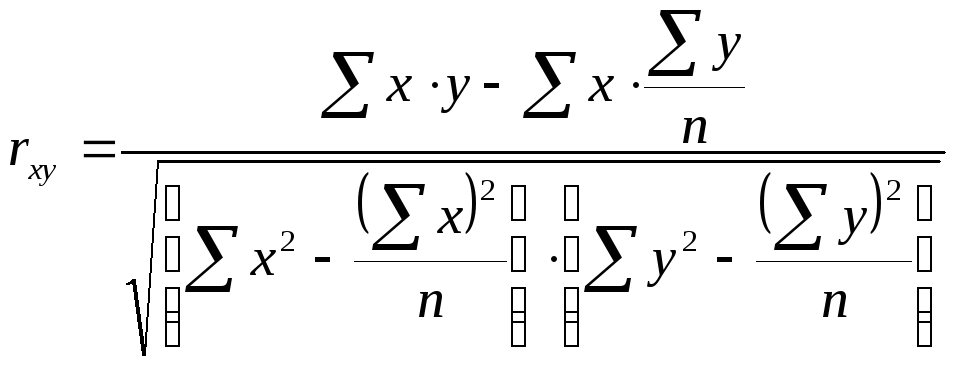