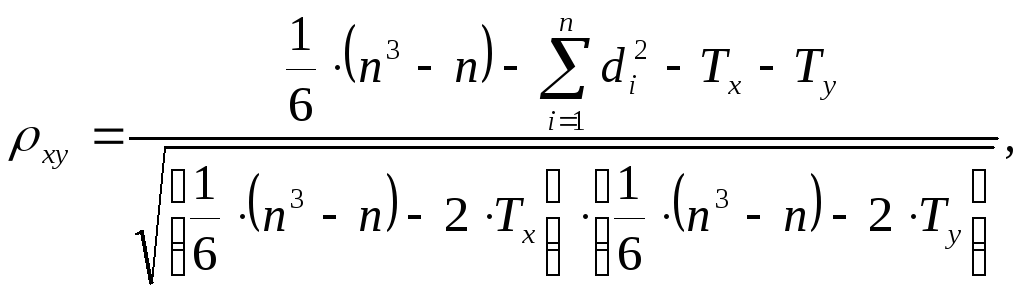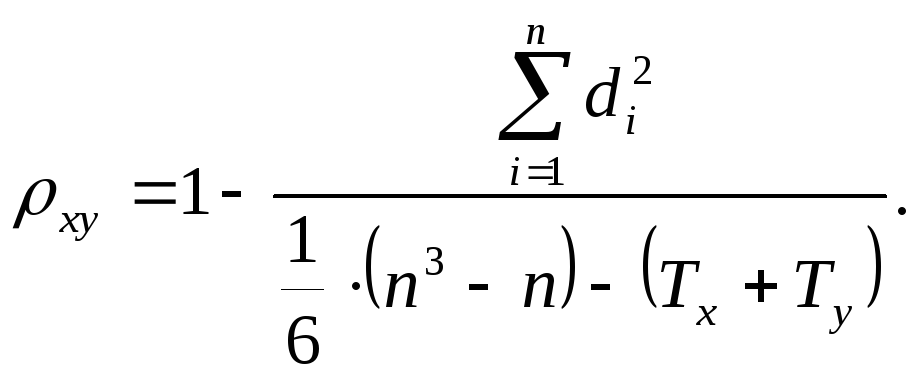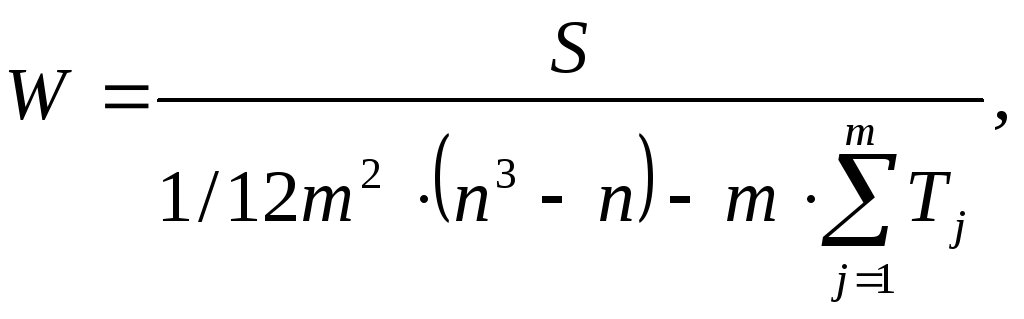ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 164
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 9 статистическое изучение взаимосвязи социально-экономических явлений
Причинность, регрессия, корреляция
9.2 Основные задачи и предпосылки применения корреляционно-регрессионного анализа
9.3 Парная регрессия на основе метода наименьших квадратов и метода группировок
9.4 Множественная (многофакторная) регрессия
9.5 Оценка существенности связи. Принятие решений на основе уравнения регрессии
9.7 Методы изучения связи социальных явлений
9.8 Непараметрические показатели связи. Ранговые коэффициенты связи
9.8 Непараметрические показатели связи. Ранговые коэффициенты связи
В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам, например знакам отклонений рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Данные коэффициенты исчисляются при условии, что исследуемые признаки подчиняются различным законам распределения.
Простейшим непараметрическим показателем
тесноты связи между двумя признаками
![]() и
и![]() являетсякоэффициент Фехнера. В
основе его расчета лежит принцип
сопоставления не абсолютных значений
признаков
являетсякоэффициент Фехнера. В
основе его расчета лежит принцип
сопоставления не абсолютных значений
признаков![]() и
и![]() ,
а их отклонений от среднего уровня.
,
а их отклонений от среднего уровня.
Применение коэффициента Фехнера в
практических расчетах основано на
предположении, что отклонения эмпирических
значений признака (![]() )
от его средней величины (
)
от его средней величины (![]() )
носят случайный характер и должны
случайным образом сочетаться с
отклонениями эмпирических значений
признака (
)
носят случайный характер и должны
случайным образом сочетаться с
отклонениями эмпирических значений
признака (![]() )
от его среднего уровня (
)
от его среднего уровня (![]() ).
).
Соотношение пар совпадений или
несовпадений знаков отклонений (![]() )
и (
)
и (![]() )
позволяет судить о наличии и степени
тесноты связи между
)
позволяет судить о наличии и степени
тесноты связи между![]() и
и![]() .
.
Коэффициент Фехнера (![]() )
определяется по формуле следующего
вида:
)
определяется по формуле следующего
вида:
![]()
|
где |
|
|
|
|
|
|
Коэффициент Фехнера может принимать
как положительные, так и отрицательные
значения в пределах от (-1) до (+1), т.е.
![]() .
.
При
![]() связь между признаками
связь между признаками![]() и
и![]() функциональная.
функциональная.
При
![]() связь отсутствует.
связь отсутствует.
Промежуточные значения коэффициента Фехнера характеризуют степень тесноты связи между двумя признаками. Знак коэффициента Фехнера свидетельствует о направлении связи между двумя признаками.
Если
![]() ,
то связь обратная, т.е. с увеличением
или снижением
,
то связь обратная, т.е. с увеличением
или снижением![]() снижается или увеличивается
снижается или увеличивается![]() .
Если
.
Если![]() ,
то связь прямая, т.е. с увеличением или
снижением
,
то связь прямая, т.е. с увеличением или
снижением![]() увеличивается или снижается
увеличивается или снижается![]() .
.
Недостатком коэффициента Фехнера, что значительно сокращает возможности его практической реализации, является равенство весов различных по абсолютной величине отклонений фактических значений признаков от их среднего уровня.
Ранговые коэффициенты связи. В качестве условных обозначений значений признаков и оценки связей между ними также используются ранги и ранговые коэффициенты связи.
Ранжирование - это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.
Ранг - это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Данные ранги называютсясвязными.
Принцип нумерации значений исследуемых признаков является основой непараметрических методов изучения взаимосвязи между социально-экономическими явлениями и процессами.
Среди непараметрических методов оценки
тесноты связи наибольшее значение имеют
ранговые коэффициенты Спирмена (![]() )
и Кендалла (
)
и Кендалла (![]() ).
Эти коэффициенты могут быть использованы
для определения тесноты связи как между
количественными, так и между качественными
признаками при условии, если их значения
упорядочить или проранжировать по
степени убывания или возрастания
признака.
).
Эти коэффициенты могут быть использованы
для определения тесноты связи как между
количественными, так и между качественными
признаками при условии, если их значения
упорядочить или проранжировать по
степени убывания или возрастания
признака.
Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле (для случая, когда нет связных рангов)
|
|
(9.45) |
|
где |
|
|
|
|
|
|
Коэффициент Спирмена принимает любые
значения в интервале
![]() .
Значимость коэффициента корреляции
рангов Спирмена проверяется на основе
1-критерия Стьюдента. Расчетное значение
критерия определяется по формуле
.
Значимость коэффициента корреляции
рангов Спирмена проверяется на основе
1-критерия Стьюдента. Расчетное значение
критерия определяется по формуле
|
|
(9.46) |
Значение коэффициента корреляции
считается статистически существенным,
если
![]() .
.
Если совокупность значений по исследуемому признаку содержит связные ранги, то коэффициент корреляции Спирмена вычисляется по формуле
|
|
(9.47) |
|
где |
|
|
|
|
|
|
На практике, если величины
![]() и
и![]() несущественно отличаются относительно
значения
несущественно отличаются относительно
значения![]() ,
пользуются формулой
,
пользуются формулой
|
|
(9.48) |
Ранговый коэффициент корреляции
Кендалла (![]() )
может также использоваться для измерения
взаимосвязи между качественными и
количественными признаками, характеризующими
однородные объекты, ранжированные по
одному принципу. Расчет рангового
коэффициента Кендалла осуществляется
по формуле:
)
может также использоваться для измерения
взаимосвязи между качественными и
количественными признаками, характеризующими
однородные объекты, ранжированные по
одному принципу. Расчет рангового
коэффициента Кендалла осуществляется
по формуле:
|
|
(9.49) |
|
где |
|
|
|
|
|
|
Расчет данного коэффициента выполняется в следующей последовательности:
значения
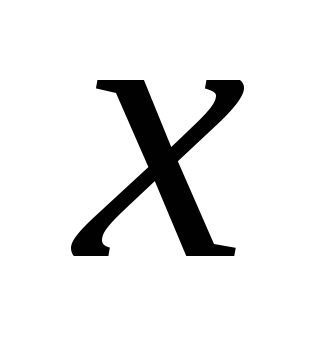 ранжируются в порядке возрастания или
убывания;
ранжируются в порядке возрастания или
убывания;значения
 располагаются в порядке, соответствующем
значениям
располагаются в порядке, соответствующем
значениям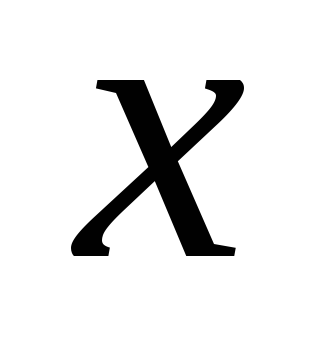 ;
;для каждого ранга
 определяется число следующих за ним
значений рангов, превышающих его
величину. Суммируя таким образом числа,
определяют величину
определяется число следующих за ним
значений рангов, превышающих его
величину. Суммируя таким образом числа,
определяют величину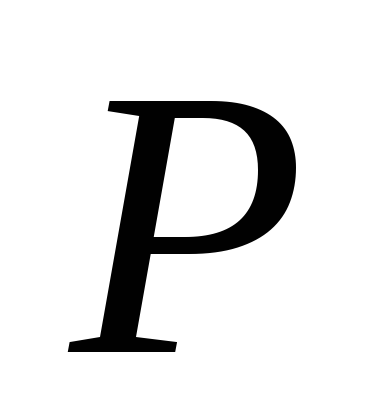 как меру соответствия последовательностей
рангов по
как меру соответствия последовательностей
рангов по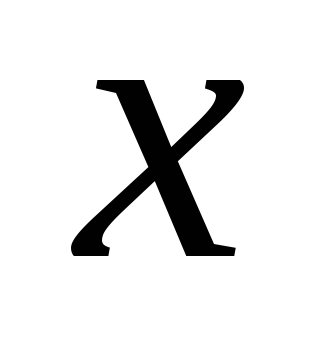 и
и и учитывают со знаком (+);
и учитывают со знаком (+);для каждого ранга
 определяется число следующих за ним
рангов, меньших его величины. Суммарная
величина обозначается через
определяется число следующих за ним
рангов, меньших его величины. Суммарная
величина обозначается через и фиксируется со знаком (-);
и фиксируется со знаком (-);определяется сумма баллов по всем членам ряда.
Если в изучаемой совокупности есть связные ранги, то расчеты необходимо проводить по следующей формуле:
|
|
(9.50) |
|
где |
|
|
Связь между признаками можно признать статистически значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0,5.
Для определения тесноты связи между
произвольным числом ранжированных
признаков применяется множественный
коэффициент ранговой корреляции
(коэффициент конкордации) (![]() ),
который вычисляется по формуле
),
который вычисляется по формуле
|
|
(9.51) |
|
где |
|
|
|
|
|
|
|
|
|
|
Значимость коэффициента конкордации
проверяется на основе
![]() -критерия
Пирсона:
-критерия
Пирсона:
|
|
(9.52) |
В случае наличия связных рангов коэффициент конкордации определяется по формуле
|
|
(9.53) |