ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 152
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 9 статистическое изучение взаимосвязи социально-экономических явлений
Причинность, регрессия, корреляция
9.2 Основные задачи и предпосылки применения корреляционно-регрессионного анализа
9.3 Парная регрессия на основе метода наименьших квадратов и метода группировок
9.4 Множественная (многофакторная) регрессия
9.5 Оценка существенности связи. Принятие решений на основе уравнения регрессии
9.7 Методы изучения связи социальных явлений
9.8 Непараметрические показатели связи. Ранговые коэффициенты связи
Коэффициенты оценки связи качественных признаков, представленных двумя градациями. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяютсякоэффициенты ассоциации и контингенции. При исследовании связи числовой материал располагают в виде таблиц сопряженности, например табл. 9.4. Для вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой).
|
Таблица 9.4 |
||
|
Таблица для вычисления коэффициентов ассоциации и контингенции |
||
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты определяются по формулам:
коэффициент ассоциации
![]()
|
|
(9.39) |
коэффициент контингенции
![]()
|
|
(9.40) |
Коэффициент контингенции всегда меньше
коэффициента ассоциации. Связь считается
подтвержденной, если
![]() или
или![]() .
.
Коэффициенты оценки связи качественных признаков, представленных несколькими градациями.
Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона-Чупрова (табл. 9.5).
|
Таблица 9.5 |
||||
|
Вспомогательная таблица для расчета коэффициента взаимной сопряженности |
||||
|
|
I |
II |
III |
Всего |
|
I |
|
|
|
|
|
II |
|
|
|
|
|
III |
|
|
|
|
|
Итого |
|
|
|
|
Этот коэффициент вычисляется по следующей формуле:
|
. |
(9.41) |
|
где |
|
|
|
|
|
|
![]()
|
|
|
|
|
|
|
|
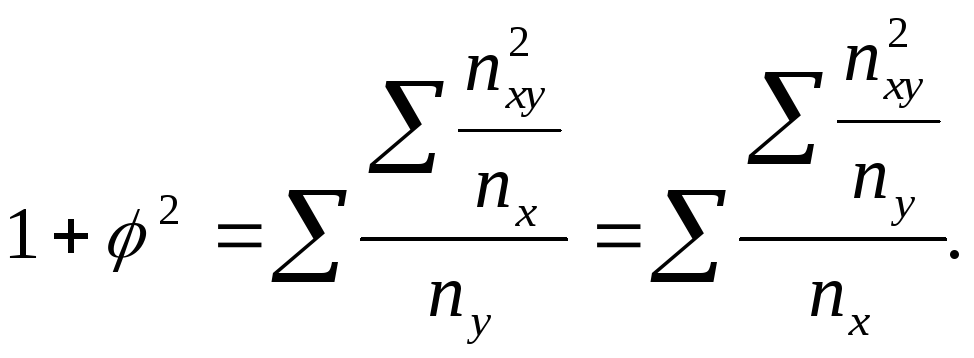
В статистике существуют модификации
коэффициента Чупрова, например,через расчет
![]() -критерия
Пирсона.Коэффициент взаимной
сопряженности (
-критерия
Пирсона.Коэффициент взаимной
сопряженности (![]() )
вычисляется по формуле
)
вычисляется по формуле
|
. |
(9.42) |
|
где |
|
|
Другой модификацией коэффициента взаимной сопряженности Чупрова является:
|
. |
(9.43) |
|
где |
|
|
|
|
|
|
|
|
|
|
Особое значение для оценки связи имеет биссериальный коэффициент корреляции, который дает возможность оценить связь между качественным альтернативным и количественным варьирующим признаками. Данный коэффициент вычисляется по формуле
|
|
(9.44) |
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
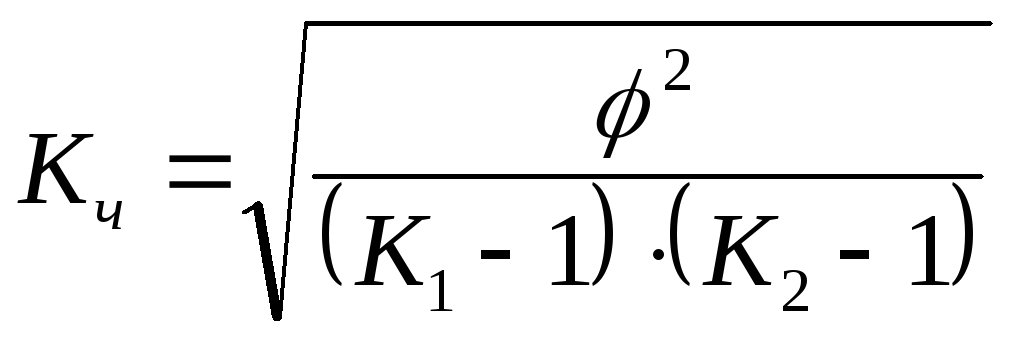 ,
,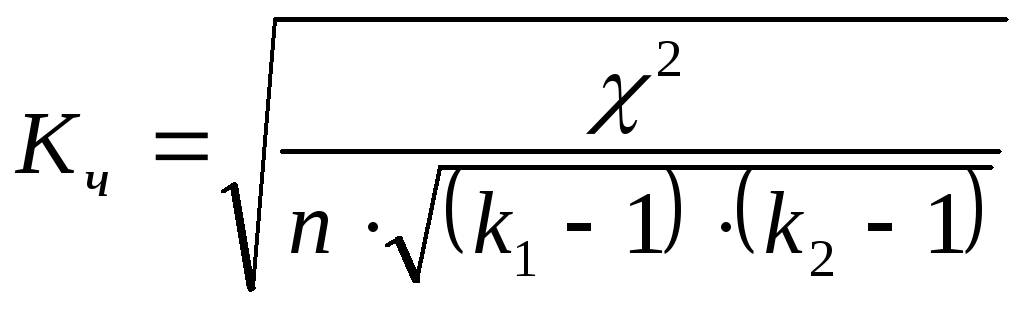 ,
,