Файл: задания по ВМиПП в матлабе.pdf

49 

элемент схемы замещения отражает обмен энергией между источником и элек-
трическим полем. Обозначение емкостного элемента приведено на рисунке 2.4, 
в. 

Если напряжение между выводами емкостного элемента изменяется сину-

соидально: 





u

Cm

C

t

sin

U

u













, 

то ток через емкостной элемент: 











































2

t

sin

I

t

cos

U

C

dt

du

C

i

u

Cm

u

Cm

C

C













, 

где амплитуды напряжения и тока связаны соотношением  

C

I

U

Cm

Cm







, 

действующие значения тока и напряжения соответственно  

C

C

C

C

x

I

C

I

U











, 

а их начальные фазы  

2

i

u











. 

Величина 

C

1

x

C







  называется  емкостным  сопротивлением,  единица  ее 

измерения – [Ом]. Комплексные значения синусоидального тока и напряжения 
емкостного элемента: 

i

j

C

C

e

I

I











 и  

u

j

C

C

e

U

U











. 

Закон Ома в комплексной форме для емкостного элемента: 

C

C

C

C

I

x

j

I

C

j

1

U

























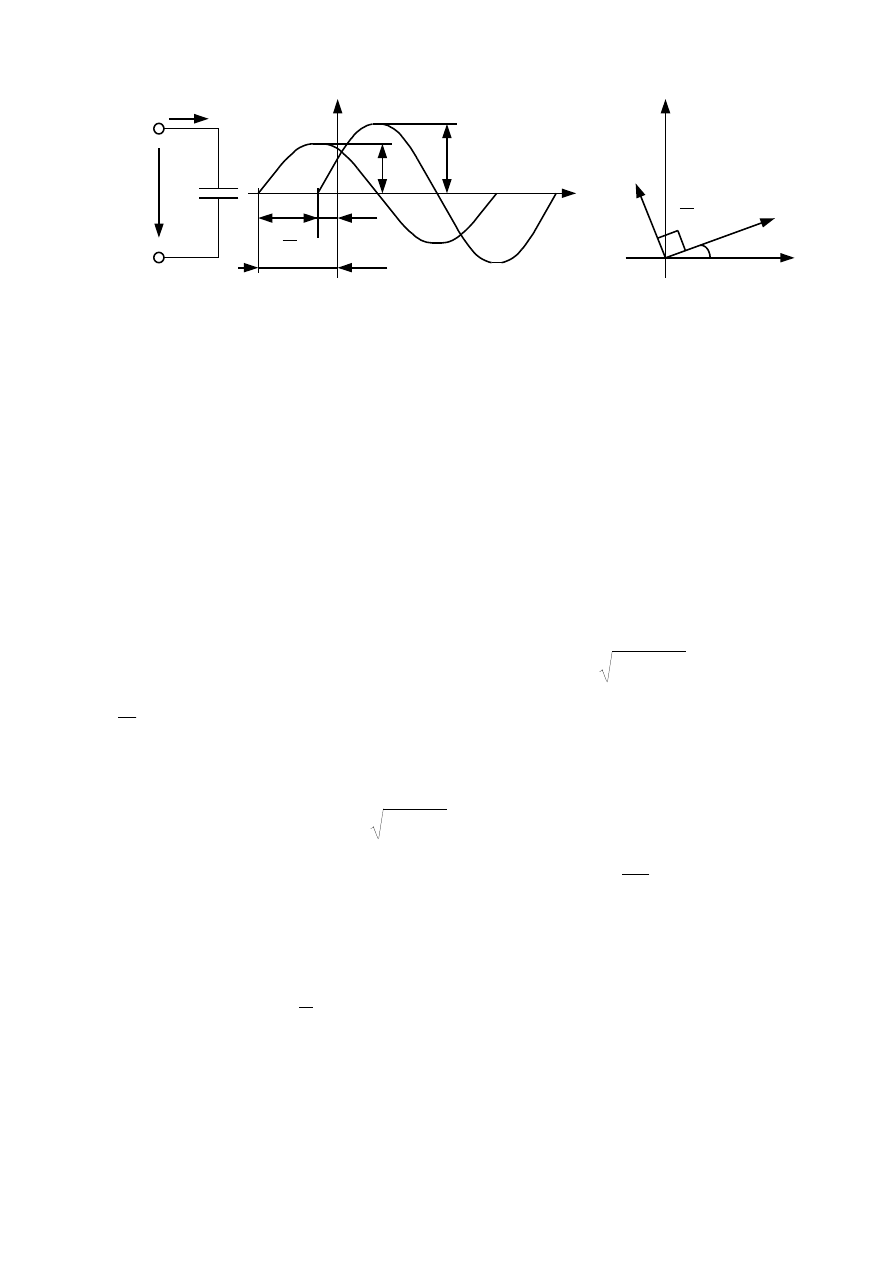
График  мгновенных  значений  напряжения  и  тока  на  емкостном  элементе 

показан на рисунке 3.7 а. Соответствующая векторная диаграмма приведена  на 
рисунке 3.7 б, из которой видно, что вектор напряжения отстает от вектора тока 
на угол 



/2. 

50 

C

u

C

i

C

i



Cm

I

Cm

U

C

U

C

I

a

б

C

u

C

i

u



2



t

1



j



u



2



Рисунок 3.7 - График изменения мгновенных значений (а) и векторная 

диаграмма (б) тока и напряжения на емкостном элементе 

3.1.4 Цепи переменного тока с последовательным и параллельным со-

единением элементов 

3.1.4.1 Последовательное соединение резистора и катушки индуктив-

ности 

Реальная катушка индуктивности кроме индуктивности обладает активным 

сопротивлением 

L

r .  Цепь,  состоящая  из  последовательно  соединенных  рези-

стора 

R

и  катушки  индуктивности 

L

  (рисунок  3.8а)  обладает  эквивалентным 

активным  сопротивлением 

L

Э

r

R

R





,  где 

L

r   -  активное  сопротивление  ка-

тушки  индуктивности  и  индуктивным  сопротивлением 

L

x

L







.  Полное  со-

противление такой цепи определяется из выражения 

2
L

2

Э

x

R

z





, а ток в цепи 

z

U

I



. Этот ток будет одинаковым для всех элементов цепи, а приложенное на-

пряжение распределится между элементами цепи, при этом напряжение на ре-
зисторе 

R

I

U

R





, совпадает по фазе с током, а напряжение на катушке индук-

тивности 

I

z

U

L

L





  (где 

2
L

2

L

L

x

r

z





  -  полное  сопротивление  реальной  ка-

тушки  индуктивности)  опережает  ток  на  угол 

L

L

L

r

x

arctg





.  Напряжение  на 

катушке можно представить в виде двух составляющих – активной 

I

r

U

L

r

L





, 

совпадающей  по  фазе  с  током,  и  реактивной  составляющей 

I

x

U

L

Lp





,  опе-

режающей ток на угол 

2



. Таким образом общее напряжение  U  питания содер-

жит  две  составляющие  –  активную 

L

r

R

a

U

U

U





  и  индуктивную 

Lp

U

.  Ре-

51 

зультирующий угол сдвига 

L

L

r

R

x

arctg







. В данном случае угол 



 считается 

положительным, так как ток 

I

 отстает от напряжения  U . 

Все соотношения для токов и напряжений этой схемы удобно представить 

в  виде  векторной  диаграммы.  Для  цепей  с  последовательным  соединением  за 
основу  диаграммы  принимается  величина,  общая  для  всех  элементов  цепи  – 
вектор тока 

I

, и относительно него под соответствующими углами откладыва-

ются векторы напряжений на отдельных элементах. Разновидностью векторных 
диаграмм  является  топографическая  векторная  диаграмма,  на  которой  каждая 
точка диаграммы соответствует определенной точке электрической цепи. Топо-
графическая  векторная  диаграмма  для  цепи  с  последовательным  соединением 
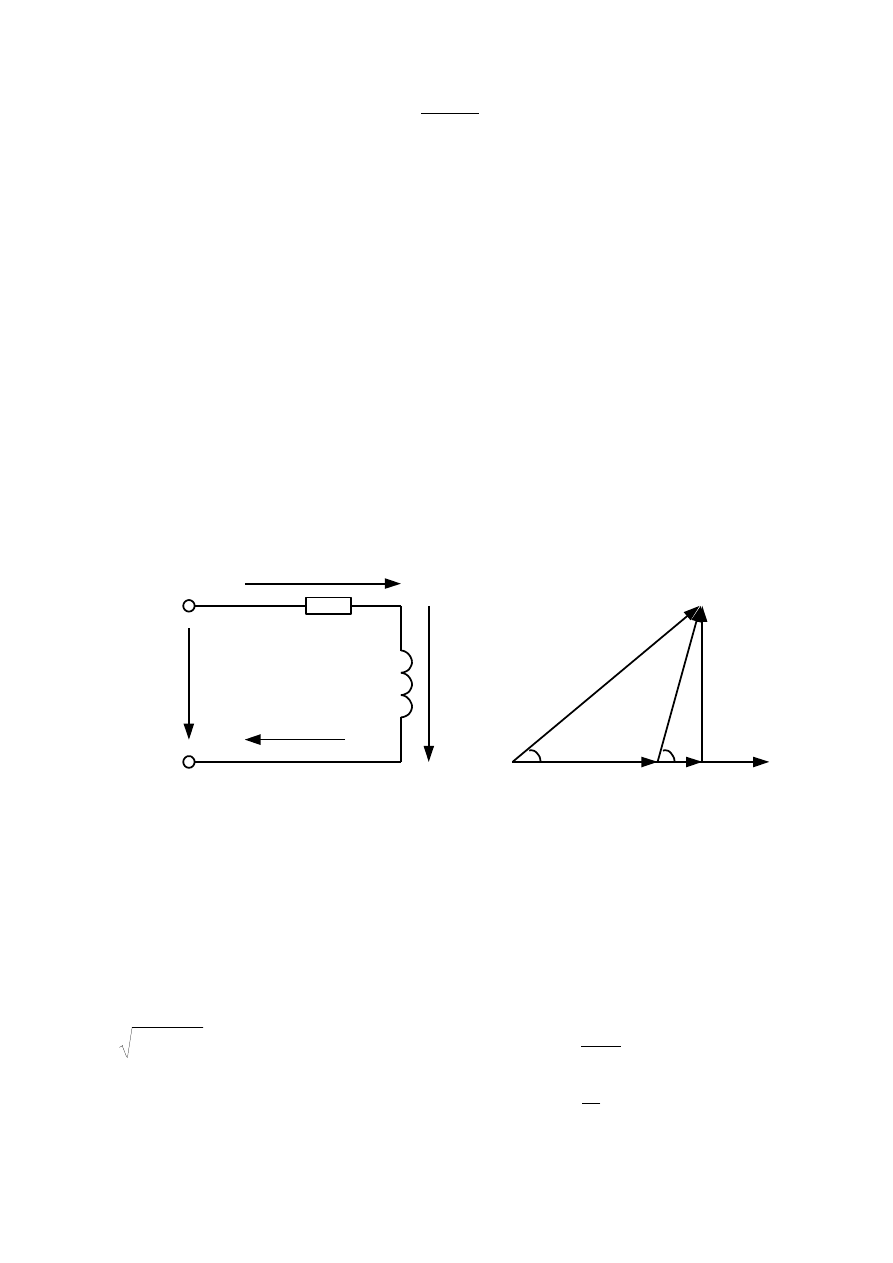
резистора  и  катушки  индуктивности  имеет  вид,  показанный  на  рисунке  3.8б. 
Эта диаграмма имеет вид треугольника напряжений, образованного векторами 

a

U , 

Lp

U

 и   U . Делением всех сторон треугольника напряжений на ток 

I

 полу-

чается подобный ему треугольник сопротивлений, а умножением сторон на ток 

I

 - треугольник мощностей. 

R

L

U

R

U

L

U

I

U

R

U

L

r

U

L

U

Lp

U

L





I

а

б

Рисунок 3.8 - Схема (а) и векторная диаграмма (б) цепи с 

последовательным соединением резистора и катушки индуктивности 

3.1.4.2 Последовательное соединение резистора и конденсатора 

Для  цепи,  состоящей  из  последовательно  соединенных  резистора  и  кон-

денсатора (рисунок 3.9 а), характерны следующие соотношения: 

2
C

2

x

R

z





-  полное  сопротивление  цепи,  где 

C

1

x

C







  -  емкостное  сопро-

тивление.  Ток,  протекающий  по  элементам  цепи: 

z

U

I



.  Падение  напряжения 

52 

на активном сопротивлении: 

R

I

U

R





, падение напряжения на конденсаторе: 

C

C

x

I

U





 является чисто емкостным (не имеет активной составляющей) и от-

стает от тока на угол 

2



. Результирующий угол сдвига между током 

I

 и напря-

жением  U : 

R

x

arctg

C





, в данном случае считается отрицательным, так как ток 

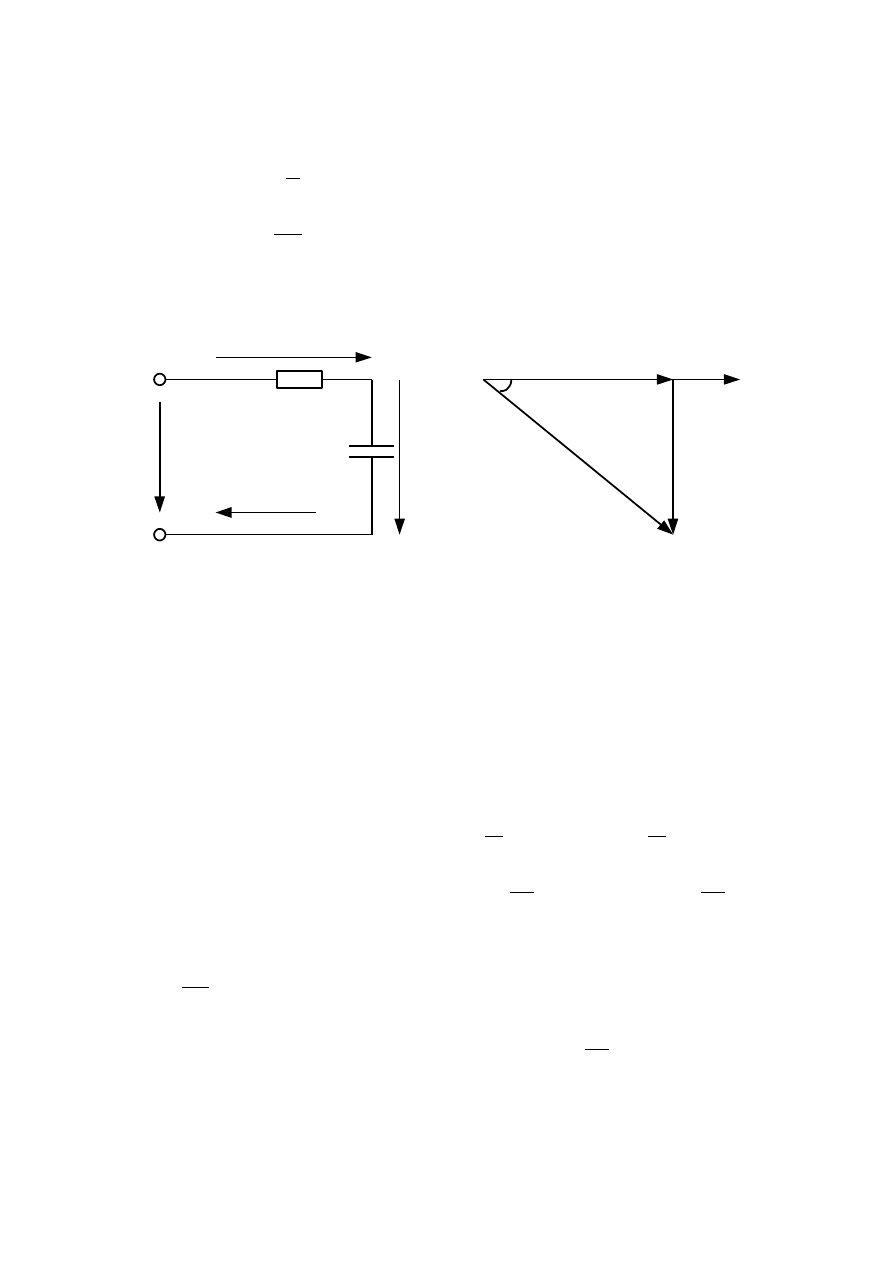
опережает напряжение. Векторная диаграмма соответствующая последователь-
ному соединению резистора и конденсатора показана на рисунке 3.9б.  

R

С

U

R

U

С

U

I

U

R

U

С

U



I

а

б

Рисунок 3.9 - Схема (а) и векторная диаграмма (б) цепи с 

последовательным соединением резистора и конденсатора 

3.1.4.3 Параллельное соединение резистора и катушки индуктивности 

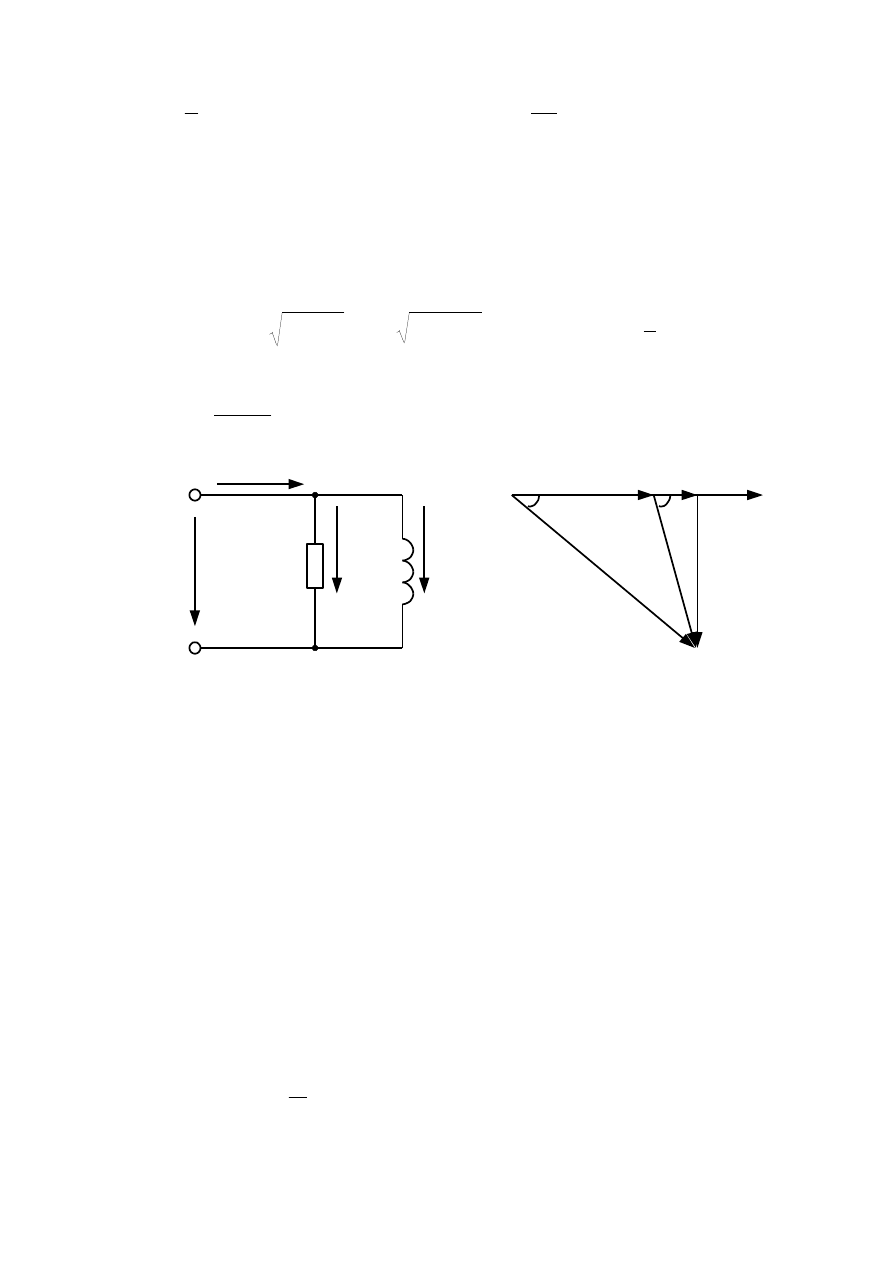
В разветвленной цепи, состоящей из параллельно соединенных резистора и 

катушки индуктивности (рисунок 3.10а), каждый ее элемент находится под од-
ним и тем же напряжением  U , которое создает в резисторе чисто активный ток, 

совпадающий по фазе с напряжением: 

U

g

R

U

I

R







, где 

R

1

g



- проводимость 

резистора. Ток в катушке индуктивности: 

U

y

z

U

I

L

L

L







, где 

L

L

z

1

y



 - полная 

проводимость катушки индуктивности. Ток 

L

I   отстает от  напряжения  на  угол  

L

L

L

r

x

arctg





 и содержит активную составляющую тока, совпадающую по фазе 

с  напряжением  U : 

L

L

L

r

g

U

cos

I

I

L











,  где 

2
L

L

L

z

r

g



  -  активная  проводи-

мость катушки, и реактивную составляющую тока, отстающую от напряжения 

53 

U на  угол 

2



:   

L

L

L

Lp

b

U

sin

I

I











, где 

2
L

L

L

z

x

b



-  реактивная проводимость 

катушки  индуктивности.  Общий  ток  в цепи 

I

  имеет  активную  составляющую 

U

g

U

)

g

g

(

I

I

I

Э

L

r

R

a

L















,  где 

L

Э

g

g

g





-  эквивалентная  активная 

проводимость  цепи,  и  реактивную  составляющую,  равную  реактивной  состав-
ляющей тока катушки 

L

L

L

Lp

p

b

U

sin

I

I

I













. Таким образом общий ток 

в цепи может быть выражен как геометрическая сумма активной и реактивной 

составляющих: 

y

U

b

g

U

I

I

I

2
L

2

Э

2
p

2
a















,  где 

z

1

y



-  эквивалентная 

полная проводимость цепи. Вектор тока 

I

 отстает от вектора напряжения  U  на 

угол 

L

L

r

R

x

arctg







. 

R

L

U

L

I

I

U

R

I

L

r

I

L

I

Lp

I

L





I

а

б

R

I

Рисунок 3.10 - Схема (а) и векторная диаграмма (б) цепи с параллельным 

соединением резистора и катушки индуктивности 

Все  эти  соотношения  представлены  на  векторной  диаграмме  (рисунок 

3.10,б). При параллельном соединении за основу диаграммы принят вектор на-
пряжения  U общий  для  всех  элементов  схемы,  и  диаграмма  имеет  вид  тре-
угольника токов. Делением всех сторон треугольника на  напряжение  U  полу-
чается подобный ему треугольник проводимостей, а умножением сторон на на-
пряжение  U - подобный треугольник мощностей. 

3.1.4.4 Параллельное соединение резистора и конденсатора 

В разветвленной цепи, состоящей из параллельно соединенных резистора и 

конденсатора (рисунок 3.11а), напряжение  U на обоих элементах схемы одина-
ково. Это напряжение создает в резисторе активный ток, совпадающий по фазе 

с  напряжением: 

R

U

I

R



.  При  этом  ток  в  конденсаторе  чисто  реактивный  (не