Добавлен: 23.10.2018
Просмотров: 7327
Скачиваний: 22
39
Таблица 2.6 – Результаты измерения
№
1
2
3
4
5
6
U, В
20
40
60
80
100
120
I, А
Построить вольт-амперную характеристику лампы накаливания. Исполь-
зуя графический метод расчета определить токи
1
I ,
2
I ,
3
I в ветвях схемы ри-
сунка 2.26 и падения напряжения на участках
ab
U
и
bc
U
, при напряжениях пи-
тания, заданных преподавателем. Результаты расчетов занести в таблицу 2.7.
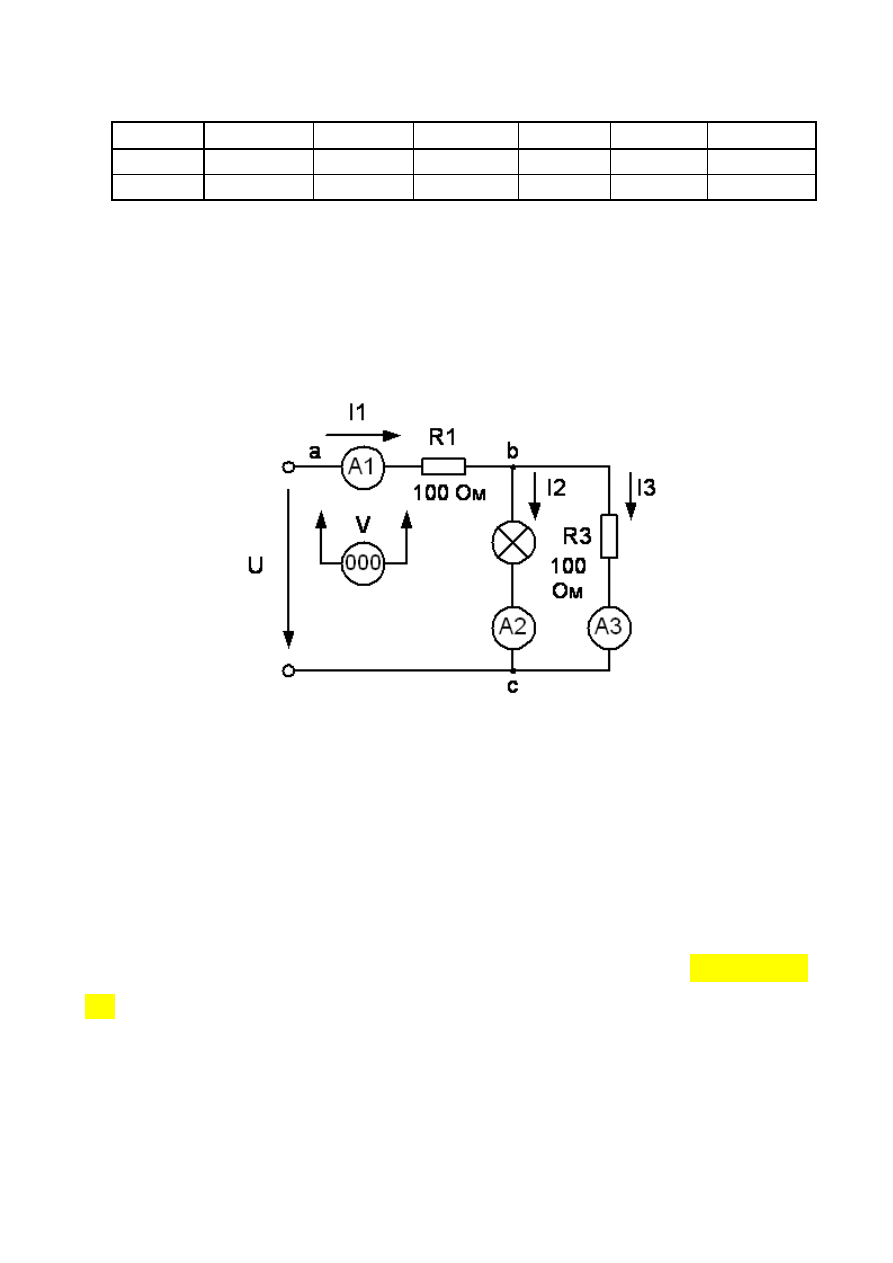
Рисунок 2.26 - Схема со смешанным соединением линейных и нелинейных
элементов
Собрать электрическую цепь на рисунке 2.26. Для измерения токов ис-
пользовать магнитоэлектрические амперметры с пределами измерений 2 А
(А1), 2 А (А2) и 1 А (А3). Для измерения напряжения использовать цифровой
вольтамперметр. Произвести измерение токов
1
I ,
2
I ,
3
I и напряжений на уча-
стках схемы
ab
U
и
bc
U
, для двух значений напряжения питания, заданных ра-
нее. Результаты измерений занести в таблицу 2.7.
Убедиться в совпадении результатов измерения с данными, полученными
при расчете схемы графическим методом.
Таблица 2.7 – Результаты эксперимента

40
№
Измерено
Вычислено
U ,
В
ab
U
,
В
bc
U
,
В
1
I ,
А
2
I ,
А
3
I ,
А
ab
U
,
В
bc
U
,
В
1
I ,
А
2
I ,
А
3
I ,
А
1
2
2.4 Контрольные вопросы к лабораторной работе № 1
1. Что понимается под ветвью, узлом, контуром электрической схемы?
2. В чем отличие между принципиальной схемой и схемой замещения?
3. Сформулируйте закон Ома для участка цепи.
4. Как определяется эквивалентное сопротивление при последовательном,
параллельном и смешанном соединении резисторов?
5. В чем заключается метод эквивалентных преобразований?
6. Сформулируйте и поясните первый и второй законы Кирхгофа.

41
3. ЛАБОРАТОРНАЯ РАБОТА №2
Электрические цепи однофазного переменного тока
Цель работы: Изучение основных законов и методов расчета линейных элек-
трических цепей однофазного переменного тока.
3.1 Теоретическое введение
Основными преимуществами переменного синусоидального тока, обу-
славливающими его широкое распространение, являются возможность переда-
чи энергии на дальние расстояния с малыми потерями, а так же простое преоб-
разование электрической энергии с помощью трансформаторов. В настоящее
время для большинства электрических сетей принята частота синусоидального
тока 50 Гц – общепромышленная частота (в США и Японии – 60 Гц). Однако в
различных отраслях промышленности встречаются другие стандарты частоты.
Например, в электротермических установках используют диапазон частот 500
Гц – 50 кГц.
3.1.1 Максимальное, действующее и среднее значения синусоидаль-
ных величин
В линейной электрической цепи при действии синусоидально изменяю-
щейся напряжения
t
sin
U
u
m
токи также имеют форму синусоиды (рисунке
3.1):
t
sin
I
i
m
,
где
f
2
- угловая частота,
T
1
f
- частота переменного тока,
- началь-
ная фаза, I
m
,
m
U – максимальные значения (амплитуда) тока, напряжения.
Средним значением синусоидальной величины считают ее среднее значе-
ние за положительный полупериод или среднее значение по модулю за период.
Например, для тока, приняв начальную фазу равной нулю, получим:
T
0
m
m
2
/
T
0
m
CP
I
2
dt
t
sin
I
T
1
dt
t
sin
I
T
2
I
.
Синусоидальный ток, протекающий в резистивном элементе с сопротивле-
нием r, вызывает нагрев этого элемента из-за выделения тепловой энергии. Та-
кую же тепловую энергию в этом же резистивном элементе можно получить
при протекании через него некоторой величины постоянного тока. Величина
этого постоянного тока равна действующему значению соответствующего си-
42
нусоидального тока. Действующее значение синусоидального тока определяет-
ся по формуле:
2
I
dt
t
sin
I
T
1
dt
i
T
1
I
m
T
0
2
2
m
T
0
2
.
Аналогично, для любой другой синусоидальной величины:
t
sin
A
a
m
,
(ЭДС, напряжение и т.д.) среднее и действующее значения определяются из
выражений:
m
m
CP
A
637
.
0
A
2
A
,
m
m
A
707
.
0
2
A
A
.
3.1.2 Способы представления синусоидальных величин
Известно несколько способов представления синусоидальных величин: в
виде тригонометрических функций, в виде графиков, в виде вращающихся век-
торов и виде комплексных чисел. Представление синусоидальных величин в
виде тригонометрических функций рассматривалось выше (
t
sin
A
a
m
),
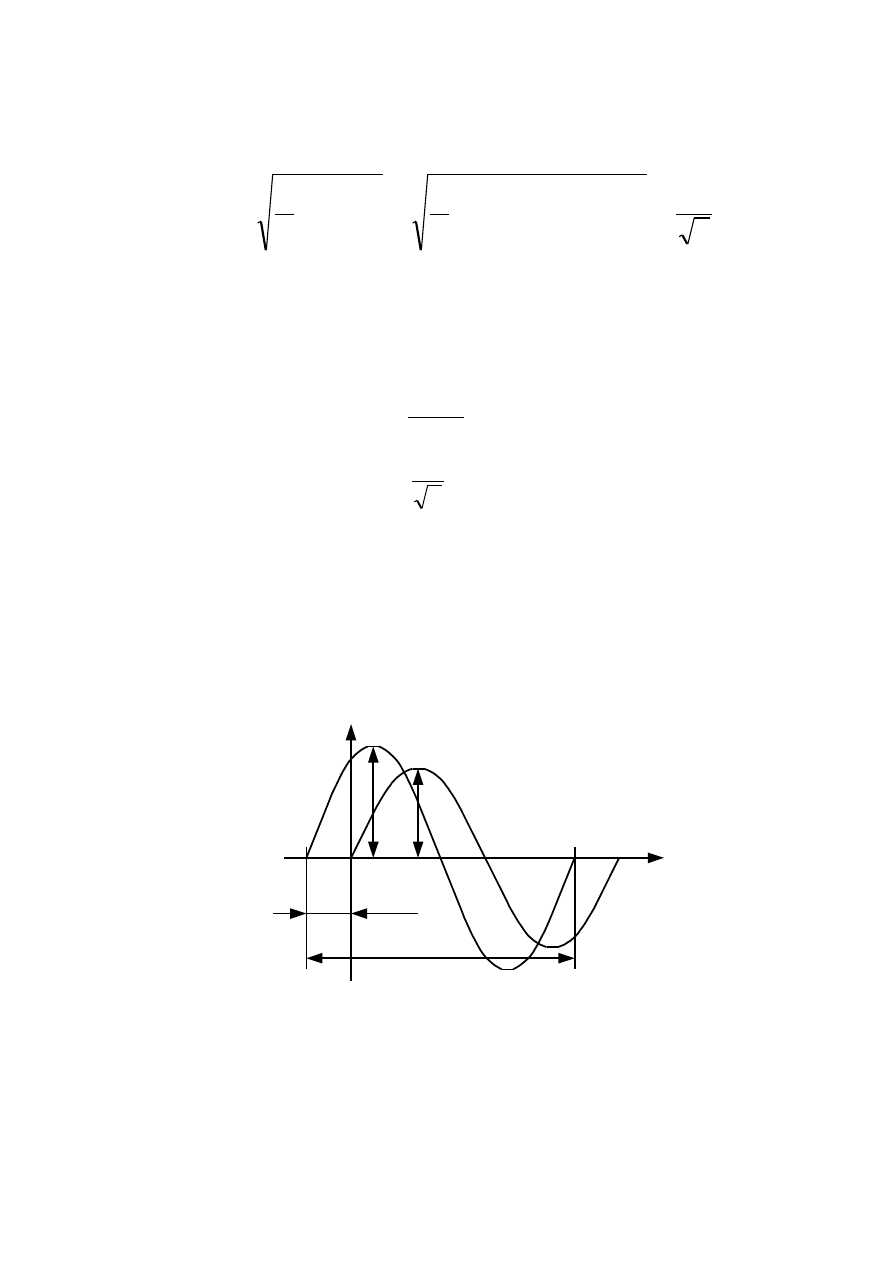
пример представления синусоидальных величин в виде графиков показан на
рисунке 3.1.
t
u
,i
m
I
Т
m
U
i
u
0
Рисунок 3.1 - Форма синусоидального тока
43
3.1.2.1 Представление синусоидальных величин вращающимися век-
торами
Для
представления
синусоидально
изменяющейся
величины
t
sin
A
a
m
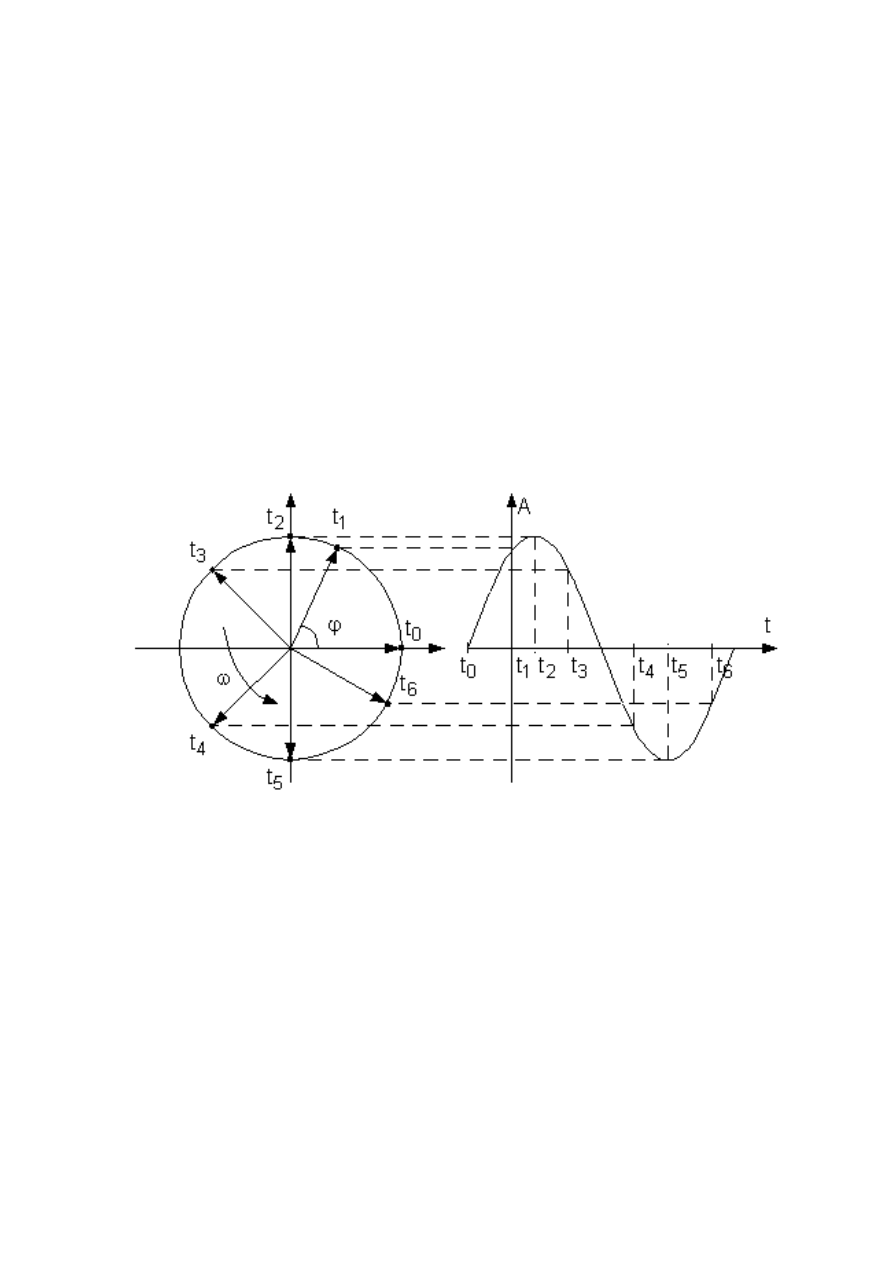
, график изменения во времени, которой показан на ри-
сунке 3.2, построим радиус-вектор этой величины
m
A
, для моментов времени
0
t
,
t
1
- t
6
. Длина этого вектора равна амплитуде синусоидальной величины
m
А
. В
момент времени
0
t , угол наклона вектора к горизонтальной оси равен
. В мо-
менты времени t
1
- t
6
, радиус вектор будет поворачиваться против часовой
стрелки на угол
t
. При этом его проекция на вертикальную ось будет
равна
t
sin
A
m
. Таким образом, синусоидально изменяющуюся величину
можно представить в виде вектора, вращающегося с постоянной угловой ско-
рость
, и имеющего длину равную амплитудному значению синусоидальной
величины.
Рисунок 3.2 - Представление синусоидальной величины вращающимся
вектором
Применение вращающихся векторов позволяет компактно представить на
одном рисунке несколько различных величин изменяющихся с одной частотой,
так как их положение (угол сдвига) друг относительно друга остается неизмен-
ным. Совокупность векторов нескольких синусоидальных величин одной час-
тоты называют векторной диаграммой. Пользуясь векторной диаграммой, сло-
жение и вычитание мгновенных значений можно заменить сложением и вычи-
танием соответствующих векторов.