Добавлен: 23.10.2018
Просмотров: 7328
Скачиваний: 22
44
3.1.2.2 Представление синусоидальных величин комплексными чис-
лами
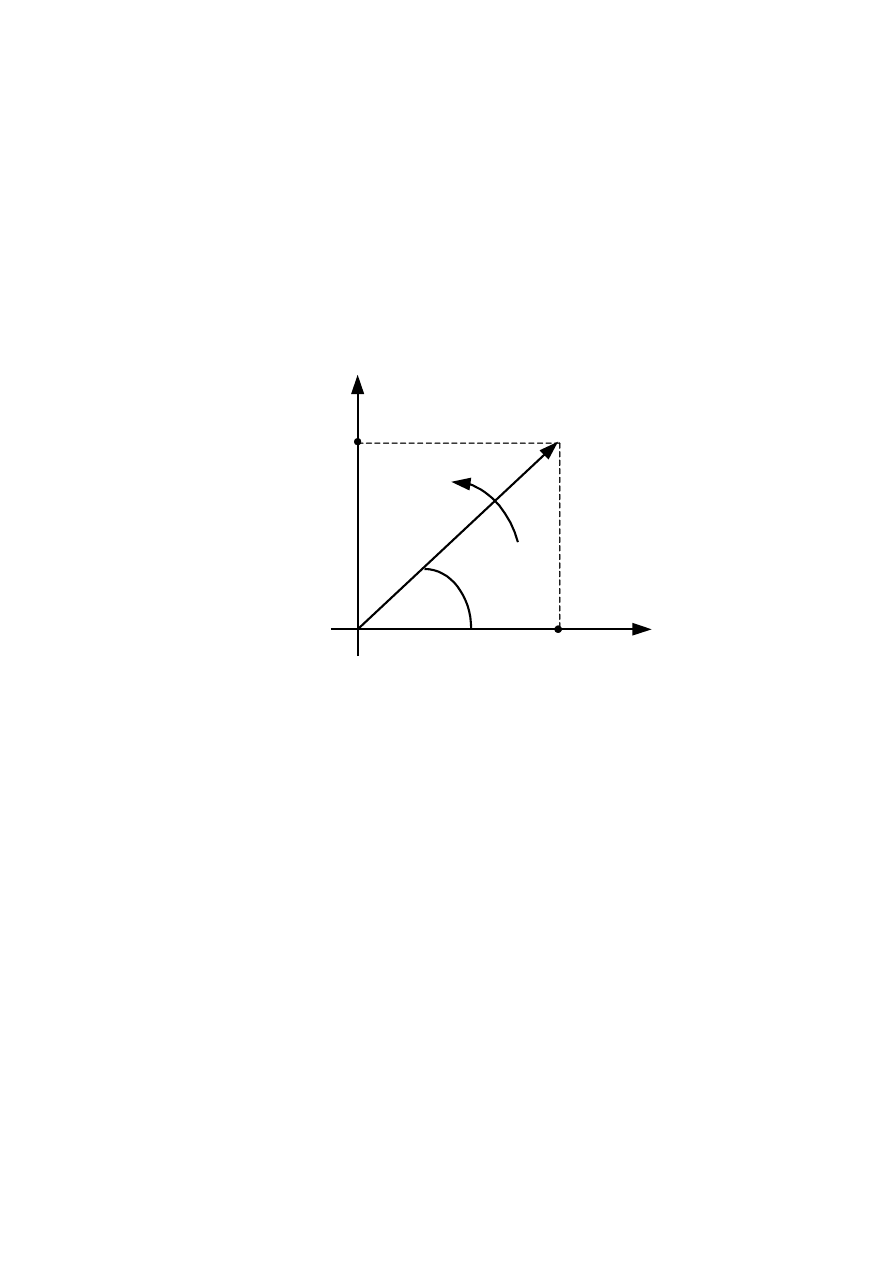
Вращающиеся векторы синусоидальных величин можно изобразить на
комплексной плоскости. При этом ось абсцисс совпадает с осью действитель-
ных чисел (ось +1), а ось ординат с осью мнимых величин (+j). Любому вектору
на комплексной плоскости соответствует определенное комплексное число (ри-
сунок 3.3). Так вращающемуся вектору, синусоидальной величины
t
sin
A
a
m
, будет соответствовать комплексное число:
t
j
j
m
t
j
m
е
е
А
е
А
t
1
j
m
I
)
I
Re(
m
)
I
Im(
m
Рисунок 3.3 - Комплексное представление
синусоидальной величины
Комплексное число, соответствующее положению вектора в начальный
момент времени (t = 0)
j
m
m
е
А
А
- называют комплексной амплитудой си-
нусоидальной величины. При увеличении во времени фазы синусоидальной
величины угол между вектором и осью растет, функцию поворота вектора на
угол
t
относительно начального положения выполняет комплексное число
t
j
е
. Для анализа синусоидальных величин имеющих одинаковую частоту
важно взаимное положение векторов в начальный момент времени, поэтому
для расчета используют только комплексные амплитуды синусоидальных вели-
чин или комплексные действующие значения. Вектор на комплексной плоско-
сти, длина которого равна действующему значению синусоидальной величины,
и соответствующее этому вектору комплексное число называют комплексным
действующим значением синусоидальной величины:

45
j
m
е
А
2
А
А
Представление синусоидальной величины комплексной амплитудой или
действующим значением аналогично представлению с помощью вращающего-
ся вектора. Однако представление синусоидальных величин в комплексной
форме позволяет применить эффективный комплексный метод расчета цепей
синусоидального тока, то есть сложение и вычитание векторов заменить сло-
жением и вычитанием комплексных чисел.
Применяются три формы записи комплексного значения синусоидальной
величины:
j
е
А
А
- показательная форма,
sin
A
j
cos
A
А
- тригонометрическая форма,
A
Im
j
A
Re
А
- алгебраическая форма,
где
A
Re и
A
Im - действительная и мнимая часть комплексного значения си-
нусоидальной величины. Переход от алгебраической формы к показательной
осуществляется по формулам:
2
2
A
Im
A
Re
А
,
A
Re
A
Im
arctg
.
Переход от показательной формы к тригонометрической осуществляется
по формуле Эйлера:
sin
j
cos
e
j
.
Сложение и вычитание комплексных величин производится в алгебраиче-
ской форме, а умножение и деление в показательной. При анализе цепей сину-
соидального тока применяют главным образом комплексные действующие зна-
чения синусоидальных величин, сокращенно их называют комплексными зна-
чениями.
3.1.3 Основные элементы цепей переменного тока
В цепях переменного тока, кроме процессов преобразования электроэнер-
гии в другие виды энергии (например в тепловую), происходит изменение энер-
гии магнитных и электрических полей. Поэтому схемы замещения цепей пере-
менного тока могут содержать активные сопротивления, индуктивные, емкост-
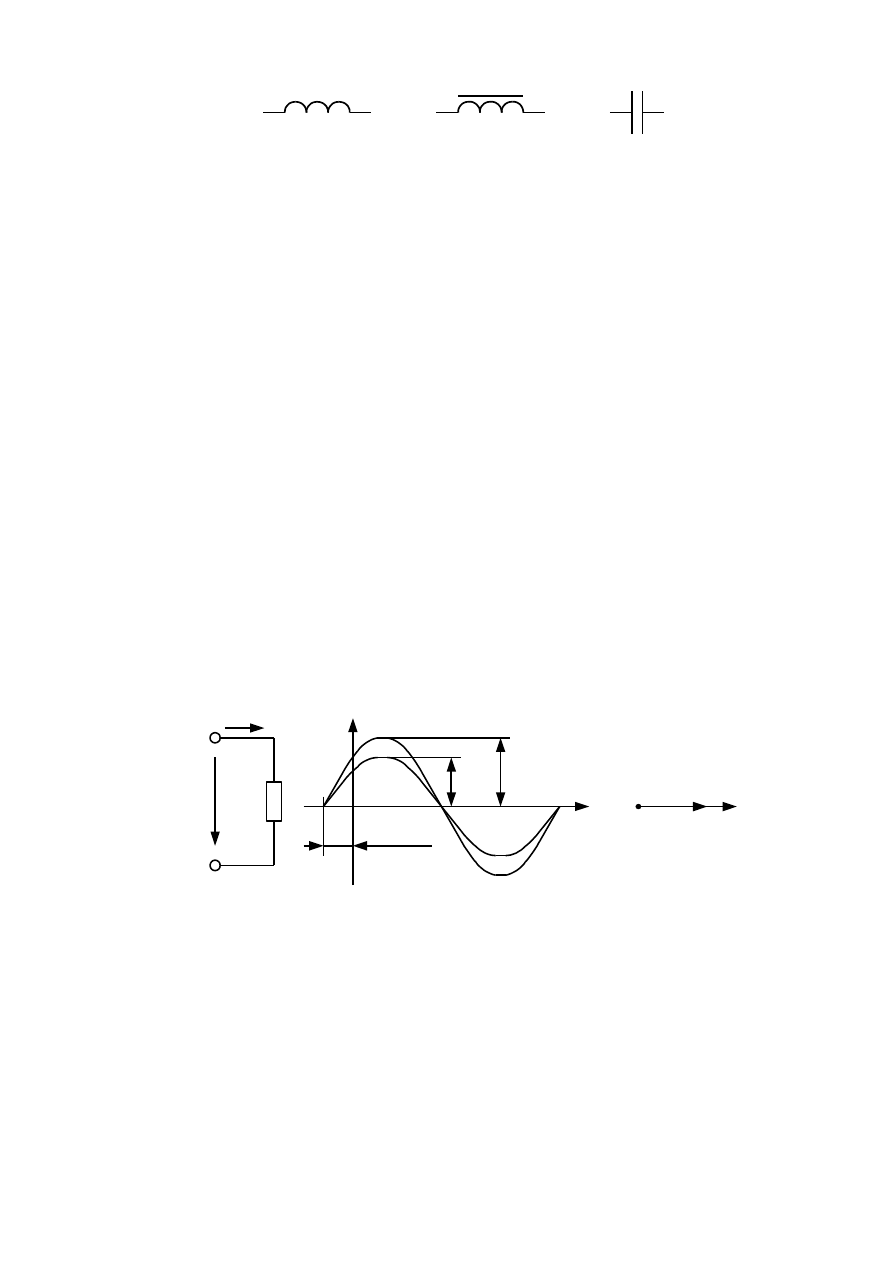
ные элементы. Обозначения основных элементов схем замещения переменного
тока приведены на рисунке 3.4.
46
а
б
в
Рисунок 3.4 - Обозначения основных элементов
цепей переменного тока
3.1.3.1
Резистивный элемент
Если ток в резистивном элементе синусоидальный
i
rm
r
t
sin
I
i
,
то по закону Ома напряжение, приложенное к элементу равно:
u
rm
i
rm
r
r
t
sin
U
t
sin
I
r
i
r
u
.
Представим ток и напряжение резистивного элемента соответствующими
комплексными значениями:
i
j
r
r
e
I
I
и
u
j
r
r
e
U
U
.
Для резистивного элемента ток и напряжение совпадают по фазе
u
i
(рисунке 3.5 а), а действующие значения напряжения и тока связаны между со-
бой соотношением
r
r
I
r
U
. С учетом этого закон Ома в комплексной форме
для резистивного элемента:
r
r
I
r
U
.
r
u
r
i
r
i
u
rm
I
rm
U
r
U
r
I
a
б
r
u
r
i
Рисунок 3.5 - График изменения мгновенных значений (а) и векторная
диаграмма (б) тока и напряжения на резистивном элементе
Соотношение между комплексными значениями тока и напряжения для
резистивного элемента наглядно показано на векторной диаграмме (рисунке 3.5
б).

47
3.1.3.2 Индуктивный элемент
Индуктивный элемент схемы замещения характеризует наличие изменяю-
щегося магнитного поля, созданного током, протекающим в цепи. В цепях пе-
ременного тока, всякое изменение тока в проводнике сопровождается измене-
нием потокосцепления
L
этого проводника, что вызывает появление ЭДС са-
моиндукции в этом элементе е
L
. Это явление получило название самоиндукции.
ЭДС самоиндукции определяется скоростью изменения собственного потокос-
цепления:
dt
d
e
L
L
.
Величина собственного потокосцепления индуктивного элемента пропор-
циональна величине тока в нем
i
L
L
, где L – собственная индуктивность
элемента. Когда магнитное поле образуется в немагнитной среде, зависимость
)
i
(
L
является линейной и индуктивность элемента
const
L
. Для катушек
индуктивности с магнитным сердечником индуктивность зависит от проте-
кающего тока. Условные графические обозначения катушек индуктивности без
сердечника и с ферромагнитным сердечником приведены на рисунке 3.4 а, б.
Направление ЭДС самоиндукции
dt
di
L
e
L
определяется знаком произ-
водной тока по времени. При увеличении тока, ЭДС самоиндукции направлена
встречно по отношению к направлению протекания тока и вычитается из при-
ложенного напряжения (препятствует увеличению тока). При уменьшении тока
направление ЭДС самоиндукции совпадает с направлением тока, ЭДС самоин-
дукции складывается с приложенным напряжением (стремится поддержать ток
постоянным).
При синусоидальном токе в индуктивном элементе
i
Lm
L
t
sin
I
i
,
по закону электромагнитной индукции напряжение на индуктивном элементе
равно:
2
t
sin
U
t
cos
I
L
dt
di
L
e
u
i
Lm
i
Lm
L
L
,
где
амплитуды
напряжения
и
тока
связаны
соотношением
Lm
L
Lm
Lm
I
x
I
L
U
, действующие значения тока и напряжения соответ-
ственно
L
L
L
L
I
x
I
L
U
, а их начальные фазы -
2
i
u
. Величина
L
x
L
называется индуктивным сопротивлением, единица ее измерения –
48
[Ом]. Комплексные значения синусоидального тока и напряжения индуктивно-
го элемента:
i
j
L
L
e
I
I
и
u
j
L
L
e
U
U
.
Закон Ома в комплексной форме для индуктивного элемента:
)
2
(
j
L
j
L
L
i
u
e
I
L
e
I
L
U
или
L
L
L
L
I
x
j
I
L
j
U
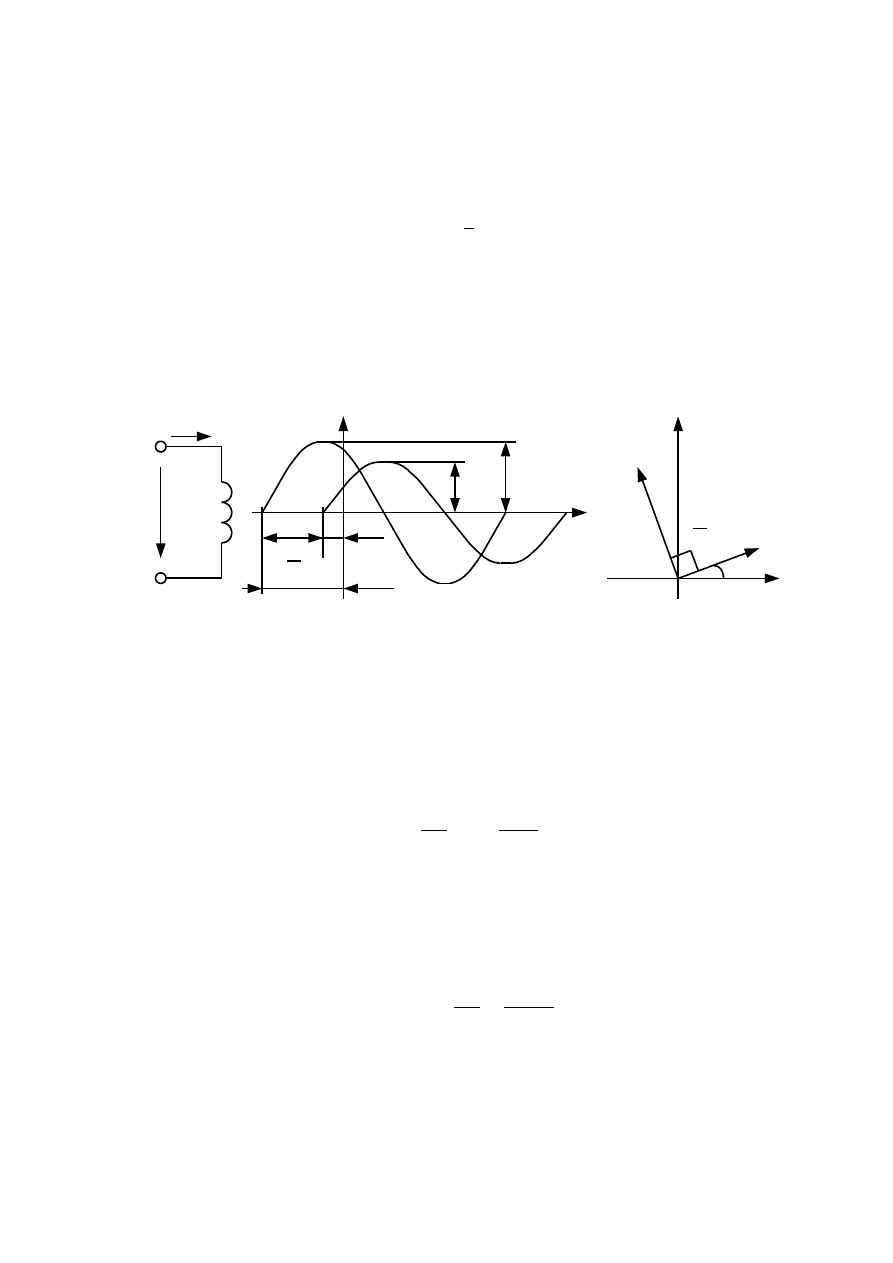
График мгновенных значений напряжения и тока на индуктивном элемен-
те показан на рисунке 3.6, а. Соответствующая векторная диаграмма приведена
на рисунке 3.6 б, из которой видно, что вектор тока отстает от вектора напря-
жения на угол
/2.
L
u
L
i
L
i
Lm
I
Lm
U
L
U
L
I
a
б
L
u
L
i
u
2
t
L
L
i,
u
1
j
i
2
Рисунок 3.6 - График изменения мгновенных значений (а) и векторная
диаграмма (б) тока и напряжения на индуктивном элементе
3.1.3.3 Емкостной элемент
Емкость учитывает изменение энергии электрического поля. Напряжение и
ток емкостного элемента связаны уравнением:
dt
du
C
dt
dq
i
C
.
Если напряжение на емкостном элементе u
C
возрастает, то ток положите-
лен. То есть в данный момент времени ток имеет направление, совпадающее с
условно положительным направлением напряжения u
C
. Заряд и энергия элек-
трического поля между обкладками конденсатора
2
u
q
2
u
C
W
C
2
C
Э
,
при этом возрастают. Энергия от источника передается электрическому полю.
Когда напряжение u
C
убывает, уменьшается и заряд, энергия запасенная в элек-
трическом поле возвращается обратно в источник. Следовательно, емкостной