Файл: ЛР Специальные главы математики.pdf

56 

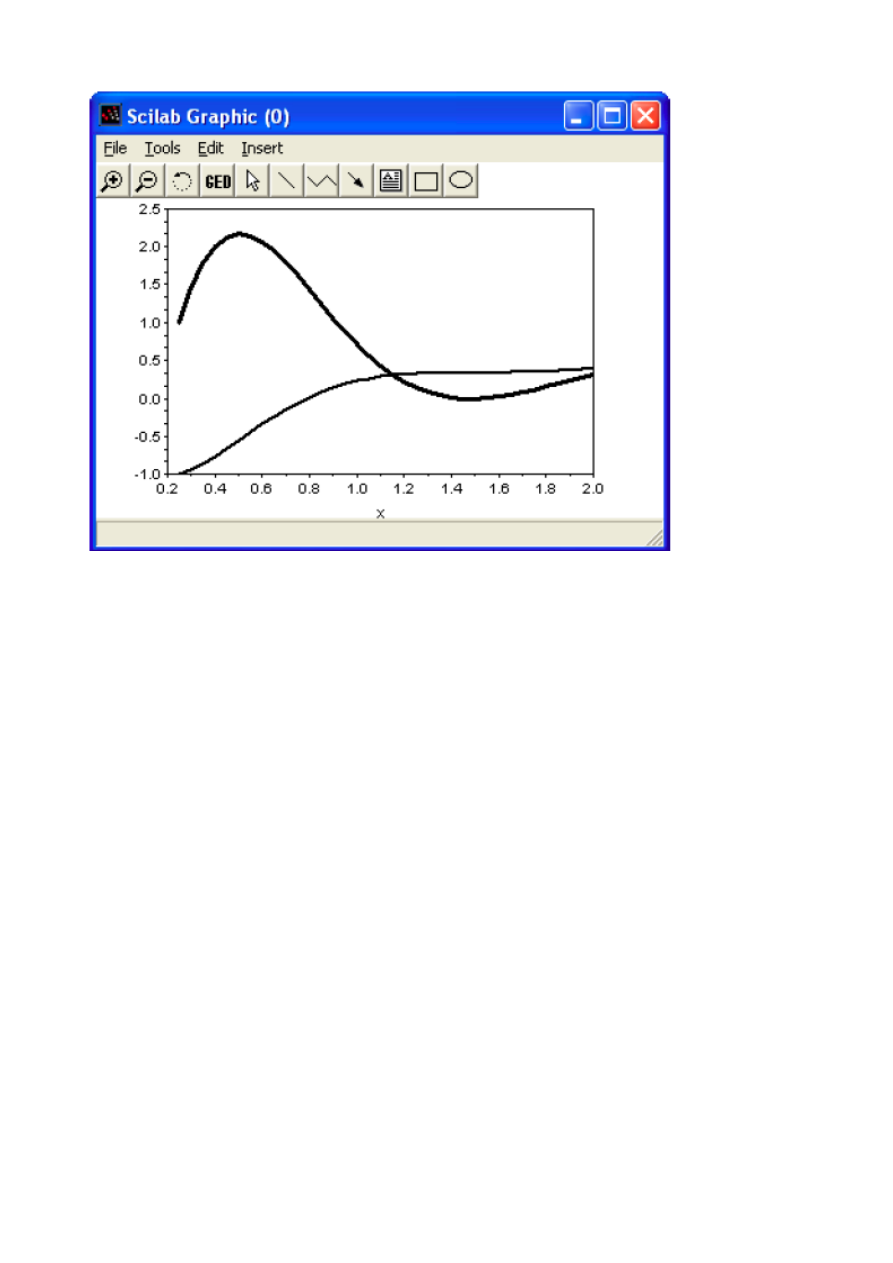
Рис.8.5. Решение задачи 8.5 

Контрольные вопросы 

1) 

Сформулируйте  задачу  Коши  для  обыкновенных  дифференциальных 

уравнений первого порядка. 

2) 

Что  является  решением  дифференциального  уравнения:  а)  в  высшей 

математике, б) в прикладной математике? 

3) 

Какие  методы  решения  дифференциальных  уравнений  называются 

одношаговыми, многошаговыми? Приведите примеры. 

4) 

Сравните решения, полученные на первом, втором шаге методами Эйлера, 

Рунге-Кутта и разложением в ряд Тейлора (трудоемкость, погрешность…). 

5) 

Как оценить погрешность применяемого метода? Как ее уменьшить? 

6) 

Сравните 

одношаговые 

и 

многошаговые 

методы 

решения 

дифференциальных  уравнений,  указав  достоинства  и  недостатки  первых  и 

вторых. 

7) 

Что  такое  экстраполяционные  и  интерполяционные  методы  (формулы) 

Адамса? 

8) 

Можно  ли  применять:  а)  только  экстраполяционные  методы  Адамса,  

б) только интерполяционные? 

КОНТРОЛЬНЫЕ ВОПРОСЫ 

1. В каком виде представляются все данные в Scilab ? 

2. Как вводятся элементы вектора-строки ? 

3. Как обратиться к блоку последовательно расположенных элементов вектора? 

4. Какие знаки используются для поэлементного умножения, деления, 

возведения в степень векторов?