Файл: ЛР Специальные главы математики.pdf

51 

Для решения дифференциальных уравнений и систем в Sciab предусмотрена 

функция:  

[y,w,iw]=ode([type],y0,t0,t [,rtol [,atol]],f [,jac] [,w,iw])  

для которой, обязательными входными параметрами являются:  
y0 - 

вектор начальных условий;  

t0 - 

начальная точка интервала интегрирования;  

t - 

координаты узлов сетки, в которых происходит поиск решения; 

f - 

внешняя функция, определяющая правую часть уравнения или системы 

уравнений ; 

у - вектор решений. 

Для того чтобы решить обыкновенное дифференциальное уравнение вида 

необходимо вызвать функцию  

y=ode(y0,t0,t,f) . 

Рассмотрим необязательные параметры функции ode:  
type - 

параметр с помощью которого можно выбрать метод решения или тип 

решаемой задачи, указав одну из строк: 

−  "adams" - 

применяют при решении дифференциальных уравнений или 

систем методом прогноза-коррекции Адамса; 

52 

−  "stiff" - 

указывают при решении жестких задач; 

−  "rk" - 

используют при решении дифференциальных уравнений или 

систем методом Рунге_Кутта четвертого порядка; 

−  "rkf" - 

указывают при выборе пятиэтапного метода Рунге_Кутта 

четвертого порядка; "fix" - тот же метод Рунге_Кутта, но с 

фиксированным шагом;  

rtol,atol - 

относительная и абсолютная погрешности вычислений, вектор, 

размерность которого совпадает с размерностью вектора y, по умолчанию 
rtol=0.00001, atol=0.0000001 

, при использовании параметров "rkf" и "fix" - 

rtol=0.001, atol=0.0001; 

jac - 

матрица, представляющая собой якобиан правой части жесткой системы 

дифференциальных уравнений, задают матрицу в виде внешней функции вида 
J=jak(t,y); 

w,iw - 

векторы, предназначенные для сохранения информации о параметрах 

интегрирования, которые применяют для того, чтобы последующие вычисления 

выполнялись с теми же параметрами. 

Рассмотрим использование функции на примере следующих задач. 

ЗАДАЧА 8.1. Решить задачу Коши 

Перепишем уравнение следующим образом: 

Далее представим его в виде внешней функции, так как показано в листинге и 

применим функцию y=ode(x0,t0,t,f), в качестве параметров которой будем 

использовать 
 f - 

ссылка на предварительно созданную функцию f(t,x); 

 t - 

координаты сетки; 

x0,t0 - 

начальное   условие x(0)=1.5; 

у - результат работы функции. 

График, моделирующий процесс, описанный заданным уравнением, 

представлен на рис.8.1. 

Листинг 8.1 
 

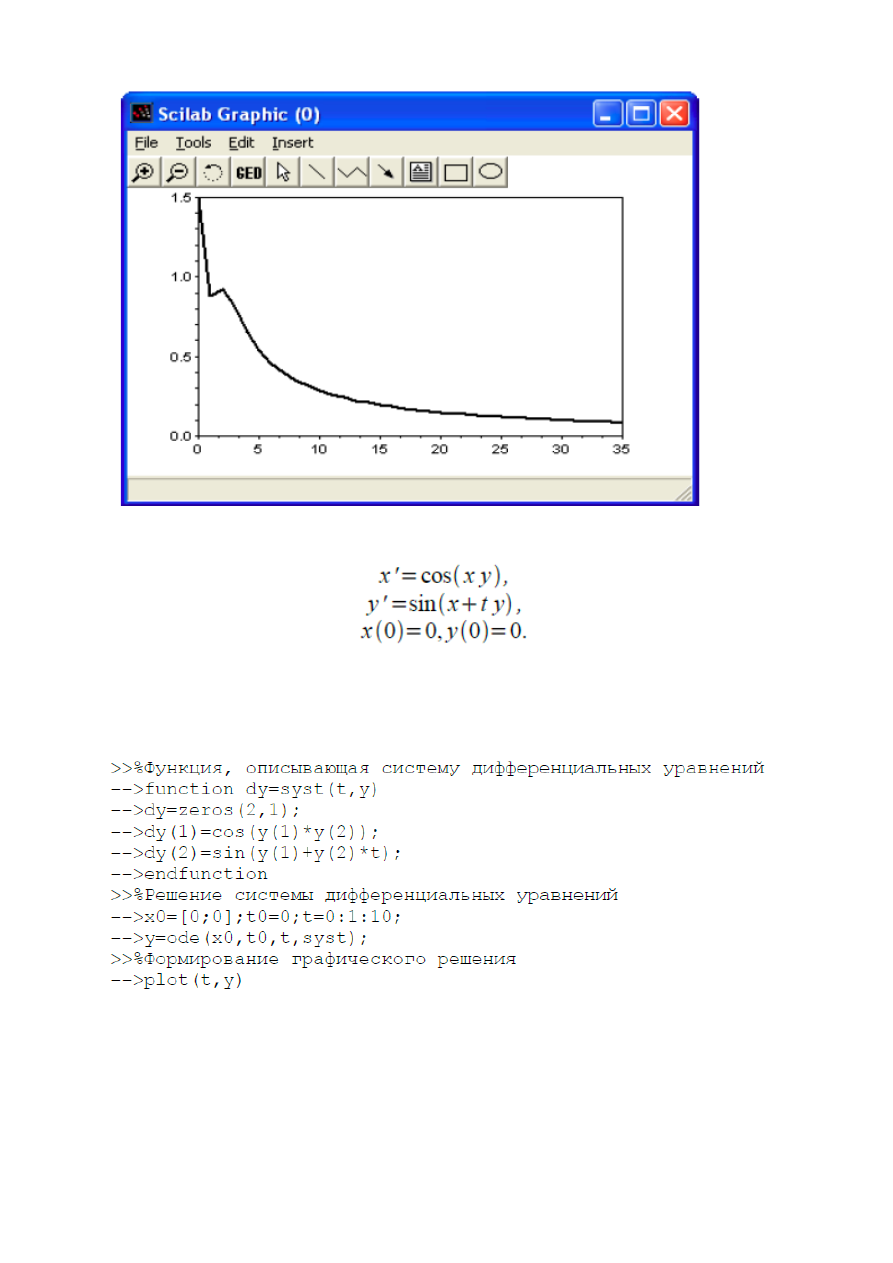
53 

из 

задачи 8.1 

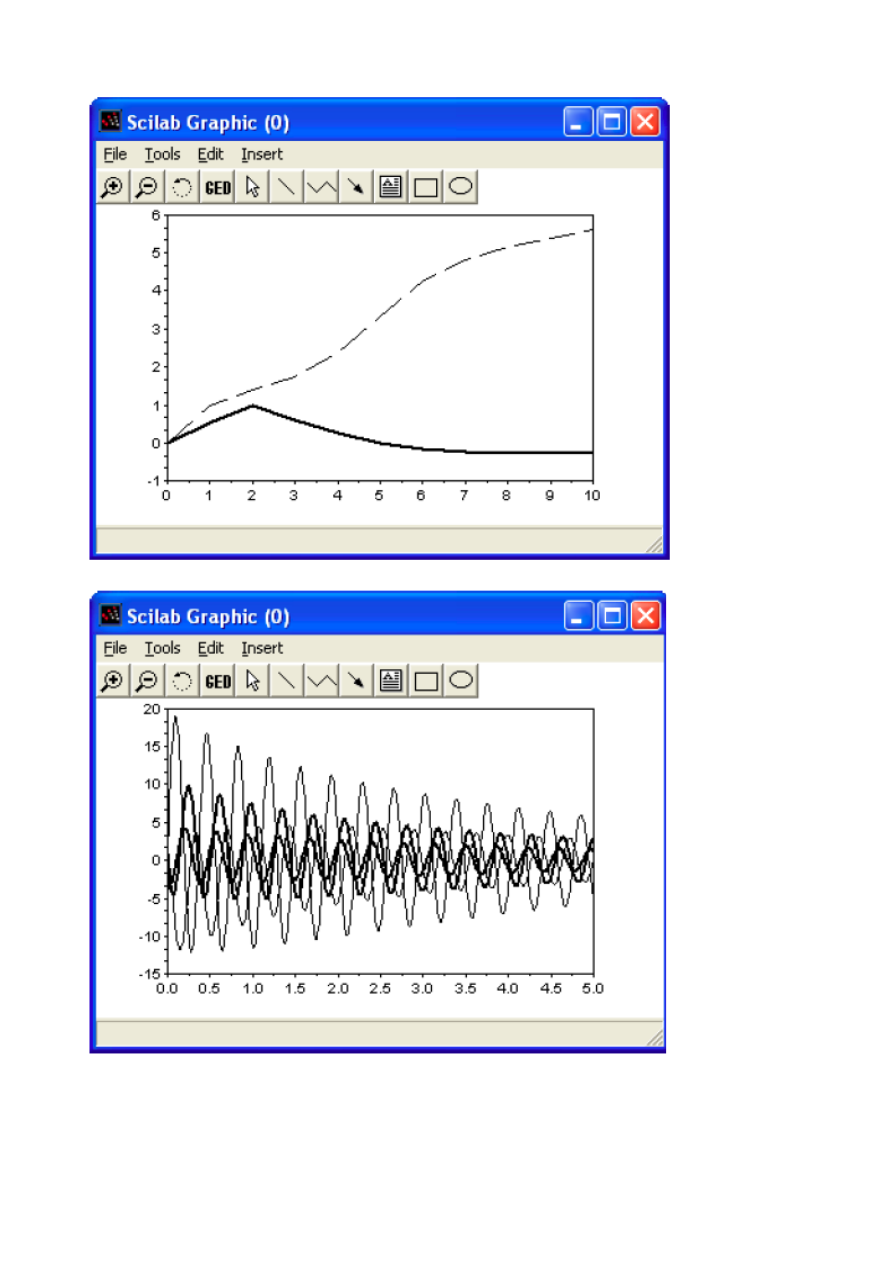
ЗАДАЧА 8.2. Решить задачу Коши 

на интервале [0; 10]. 

Листинг 8.2 содержит функцию, описывающую заданную систему 

обыкновенных дифференциальных уравнений и команды Sciab необходимые для 

ее численного и графического решения (рис.8.2). 

Листинг 8.2 

54 

Рис. 8.2. Решение задачи 8.2 

Рис. 8.3. Графическое решение жесткой системы 

ЗАДАЧА 8.3. Найти решение задачи Коши для следующей жесткой системы: 

55 

Решение системы показано в листинге 8.3.  

Графическое решение показано на рис. 8.3. 

Листинг 8.3 

ЗАДАЧА 8.5. Решить следующую краевую задачу 

на интервале [0.25; 2]. 

Преобразуем уравнение в систему, сделав замену: 

Составим функцию вычисления системы и решим ее так, как показано в листинге 

8.5. График решения приведен на рис. 8. 5. 

Листинг 8.5