Добавлен: 19.10.2018
Просмотров: 3421
Скачиваний: 9

6
Оглавление
Лабораторная работа №1 .................................................................................................... 6
Лабораторная работа №2 .................................................................................................. 18
Лабораторная работа №3 .................................................................................................. 24
Лабораторная работа №4 .................................................................................................. 28
Лабораторная работа №5 .................................................................................................. 34
Литература 37

7
Предисловие
Цель дисциплины ”Прикладная математика” - изучение методологии
приложений фундаментальных научных достижений в математике и
информатике к решению прикладных задач с учетом возрастающих
возможностей компьютерной техники и современных компьютерных
технологий.
Выполнение лабораторных работ направлено на формирование и проверку
освоения компетенций, предусмотренных рабочей программой дисциплины:
ПК-9
способностью получать и обрабатывать информацию из различных
источников, используя современные информационные технологии и
критически ее осмысливать
(код и наименование)
В результате изучения дисциплины (модуля) обучающийся должен:
Знать:
-
о точных и приближенных методах решения;
-
о связи задач дифференциального и интегрального исчисления;
-
основные понятия и методы решения уравнений математической физики;
возможные сферы их приложений;
Уметь:
-
применять теорию дифференциальных уравнений в частных производных в
решении научных задач;
-
применять математические модели для типичных базовых задач и проводить
необходимые расчеты в рамках построенных моделей.
Владеть:
-
навыками применения математических методов в прикладных задачах;
навыками использования аналитического и приближенного решения
дифференциальных уравнений в частных производных.
ПК-12 способностью использовать современные достижения науки и
передовых информационных технологий в научно-исследовательских
работах
(код и наименование)
В результате изучения дисциплины (модуля) обучающийся должен:
Знать:
-
современные тенденции развития, научные и прикладные достижения
прикладной математики и информатики
-
методологию построения математических моделей явлений и объектов,
относящихся к профилю деятельности, с использованием аппарата
прикладной математики
Уметь:
-
строить математические модели явлений и объектов, относящихся к
профилю деятельности
Владеть:
-
математическим аппаратом для разработки математических моделей явлений
и объектов, относящихся к профилю деятельности

8
Материал дисциплины предназначен для использования в курсах, связанных с
постановкой и решением реальных задач (например, различные разделы
теоретической и прикладной механики, расчет строительных конструкций), с
построением математических моделей физических процессов, верификацией
гипотез, теоретических моделей и т.д. Знания, полученные в процессе изучения
дисциплины, могут быть использованы в курсах профильной направленности.
К основным задачам, дисциплины следует отнести:
–
изучение основных понятий дисциплины;
–
изучение современных численных методов;
–
изучение возможностей различных численных алгоритмов, методов,
особенностей их применения при решении прикладных задач;
–
различные численные методы, их характеристики и свойства, особенности
применения этих методов для решения практических задач.
Объектом изучения научной и учебной дисциплины " Прикладная математика
" являются исследование практических задач в области строительства.
Лабораторная работа №1
Тема: Выполнения математических, инженерных и технических расчетов
в системе компьютерной математики SciLab.
1.
Цель работы
Закрепление, углубление и совершенствование знаний и практических навыков
работы на персональном компьютере с использованием современных
компьютерных технологий.
2.
Учебные вопросы, подлежащие рассмотрению:
−
Основы работы в Scilab
−
Функции в Scilab
−
Массивы в Scilab
−
Построение двумерных графиков
3.
Порядок выполнения работы
Основы работы в Scilab
Scilab -
это система компьютерной математики, которая предназначена для
выполнения инженерных и научных вычислений, таких как:
-
решение нелинейных уравнений и систем;
-
решение задач линейной алгебры;
-
решение задач оптимизации;
-
дифференцирование и интегрирование;
-
обработка экспериментальных данных (интерполяция и аппроксимация,
метод наименьших квадратов);
-
решение обыкновенных дифференциальных уравнений и систем.
Кроме того, Scilab предоставляет широкие возможности по созданию и
редактированию различных видов графиков и поверхностей.
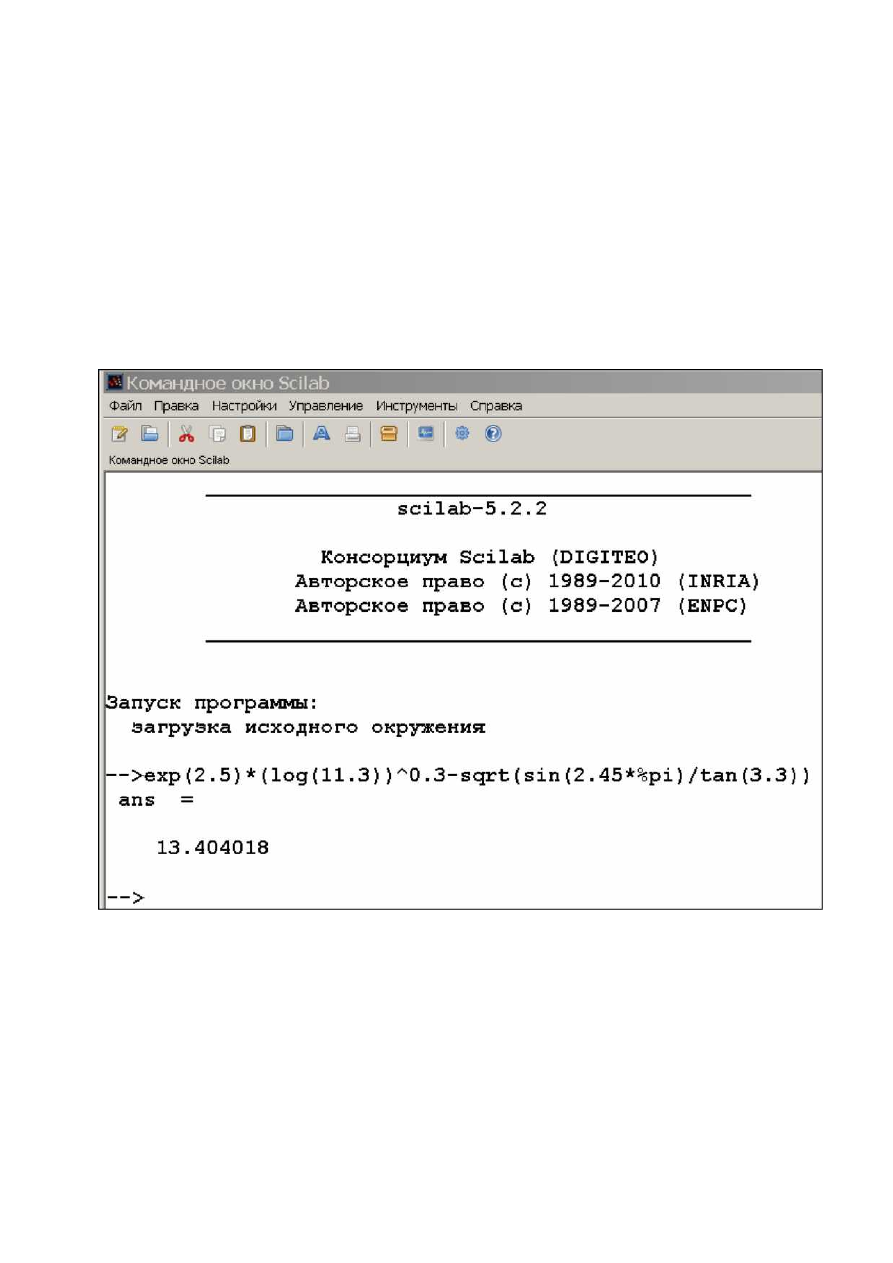
После запуска Scilab на экране появится основное окно приложения. Окно
содержит меню, панель инструментов и рабочую область. Признаком того, что
система готова к выполнению команды, является наличие знака приглашения
>
в
командной строке, после которого расположен активный (мигающий) курсор.
9
Ввод команд в Scilab осуществляется с клавиатуры. Нажатие клавиши Enter
заставляет систему выполнить команду и вывести результат (рис. 1).
Исправить что-либо в области просмотра уже выполненных команд нельзя.
Однако все ранее вводимые команды сохраняются в специальной области
памяти, и их можно просмотреть с помощью клавиш клавиатуры | |. Например,
нажатие клавиши | один раз в пустой в командной строке отразит предыдущую
выполненную команду, которую можно отредактировать и запустить заново.
Если набираемое выражение очень длинное, его можно продолжить на
следующей строке, для этого в месте прерывания нужно набрать три точки без
пробелов, а затем продолжить набор выражения на следующей строке.
Для подавления вывода на экран результатов промежуточных вычислений, в
конце команды используется точку с запятой «;».
Рис. 1. Командная строка SciLab
Арифметические операции выполняются в обычном порядке: свойственном
языкам программирования:
−
действия в скобках;
−
вычисление функции;
−
возведение в степень
^
;
−
умножение * и деление слева направо / (5/2=2.5) и справа налево \ (5\2=0.4);
−
сложение и вычитание +, -.
Для изменения порядка вычислений используйте скобки.

10
Переменные в Scilab. Любая переменная до использования в формулах и
выражениях должна быть определена. Для этого используется оператор
присваивания «=», который в общем виде записывается
Имя переменной = Значение выражения
Действие оператора: в переменную, имя которой указано слева, будет записано
значение выражения, указанного справа.
Примечание 1. Имя переменной не должно совпадать с именами встроенных
процедур, функций и встроенных переменных системы и может содержать до 24
символов.
Примечание 2. Система различает большие и малые буквы в именах
переменных, т.е. ABC, abc, Abc, aBc - это имена разных переменных.
Примечание 3. Выражение в правой части оператора присваивания может быть
числом, арифметическим выражением, строкой символов или символьным
выражением. Если переменная является символьной, то выражение в правой
части оператора присваивания следует брать в одинарные кавычки.
Примечание 4. Если для сохранения результата операции переменная
пользователем не назначена, то SciLab определяет временную переменную ans,
которую можно использовать в дальнейших вычислениях.
Системные переменные в SciLab начинаются с символа %:
%i -
мнимая единица;
%pi -
число пи (3.1415926);
%е - экспонента 1 (2.7182818);
%inf -
машинный символ бесконечности;
%NaN -
неопределенный результат (0/0 и т.п.);
%eps -
условный ноль (2.220Е-16)
Вывод в Scilab. По умолчанию результат выводится с восемью значащими
цифрами после запятой. Для контроля вывода применяют команду printf с
заданным форматом, который соответствует правилам, принятым для этой
команды в языке С (рис. 2).
Текущий документ, отражающий работу пользователя с системой Scilab,
содержащий строки ввода, вывода и сообщения об ошибках, принято называть
сессией. Значения всех переменных, вычисленные в течение текущей сессии,
сохраняются в специально зарезервированной области памяти, называемой
рабочим пространством системы. Определения всех переменных и функций,
входящих в текущую сессию можно сохранить в виде файла, саму сессию
сохранить нельзя.