Добавлен: 19.10.2018
Просмотров: 3422
Скачиваний: 9

46
y
f x a a
a
m
= ( ; , ,...,
),
1
2
(где
a a
a
m
1
2
,
,...,
-
параметры), значения которой при
x
x
i
=
возможно мало
отличались бы от опытных значений
y i
n
i
(
, ,..., )
= 1 2
.
Метод наименьших квадратов позволяет по экспериментальным данным
подобрать такую аналитическую функцию, которая проходит настолько близко к
экспериментальным точкам, насколько это возможно.
Согласно методу наименьших квадратов наилучшими коэффициентами
a a
a
m
1
2
,
,...,
считаются те, для которых сумма квадратов отклонений найденной
эмпирической функции от заданных значений функции
[
]
S a a
a
f x a a
a
y
m
i
m
i
i
n
(
,
,...,
)
( ;
,
,...,
)
1
2
1
2
1
2
=
−
=
∑
будет минимальной.
Нахождение коэффициентов
a
i
сводится к решению системы.
a
0
n + a
1
Σ x
i
+ a
2
Σ x
i
2
+ ... + a
k
Σ x
i
k
=
Σ y
i
a
0
Σ x
i
+
a
1
Σ x
i
2
+ a
2
Σ x
i
3
+ ... + a
k
Σ x
i
k+1
=
Σ x
i
y
i
…………………………………………………..
a
0
Σ x
i
k
+
a
1
Σ x
i
k+1
+ a
2
Σ x
i
k+2
+ ... + a
k
Σ x
i
2k
= Σ x
i
k
y
i
Построение эмпирической формулы состоит из двух этапов: выяснение
общего вида этой формулы и определение ее наилучших параметров.
Эта система упрощается, если эмпирическая формула линейна
относительно параметров
a
i
, тогда система - будет линейной.
Конкретный вид системы зависит от того, из какого класса эмпирических
формул мы ищем зависимость. В случае линейной зависимости
y
a
a x
=
+
1
2
система примет вид:
a n a
x
y
a
x
a
x
x y
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
n
1
2
1
1
1
1
2
2
1
1
+
=
+
=
=
=
=
=
=
∑
∑
∑
∑
∑
,
.
Эта линейная система может быть решена любым известным методом
(методом Гаусса, простых итераций, формулами Крамера).
Для реализации этой задачи в Scilab предусмотрена функция

47
[a,S] = datafit(F,z,c),
Где F – аппроксимирующая функция, параметры которой необходимо подобрать;
z –
матрица исходных данных;
с – вектор начальных приближений;
а – вектор коэффициентов;
S –
сумма квадратов отклонений измеренных значений от расчетных
Вид аппроксимирующей функции, подбирается как наиболее подходящий для
заданных экспериментальных данных, это может быть:
-
Линейная,
-
Логарифмическая,
-
Полиномиальная,
-
Экспоненциальная и др.
Чаще в качестве аппроксимирующей функции выбирают полином
необходимой степени.
Пример. Пусть в результате эксперимента были получены некоторые данные,
отображенные в виде таблицы. Требуется построить аналитическую
зависимость, наиболее точно описывающую результаты эксперимента.
x
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
y
0.57 0.70 0.89 1.10 1.32 1.50 1.58 1.40 1.32 1.10 0.90
В качестве функции аппроксимирующей данные эксперимента следует взять
полином третьей степени, у которого четыре коэффициента, которые
необходимо найти.
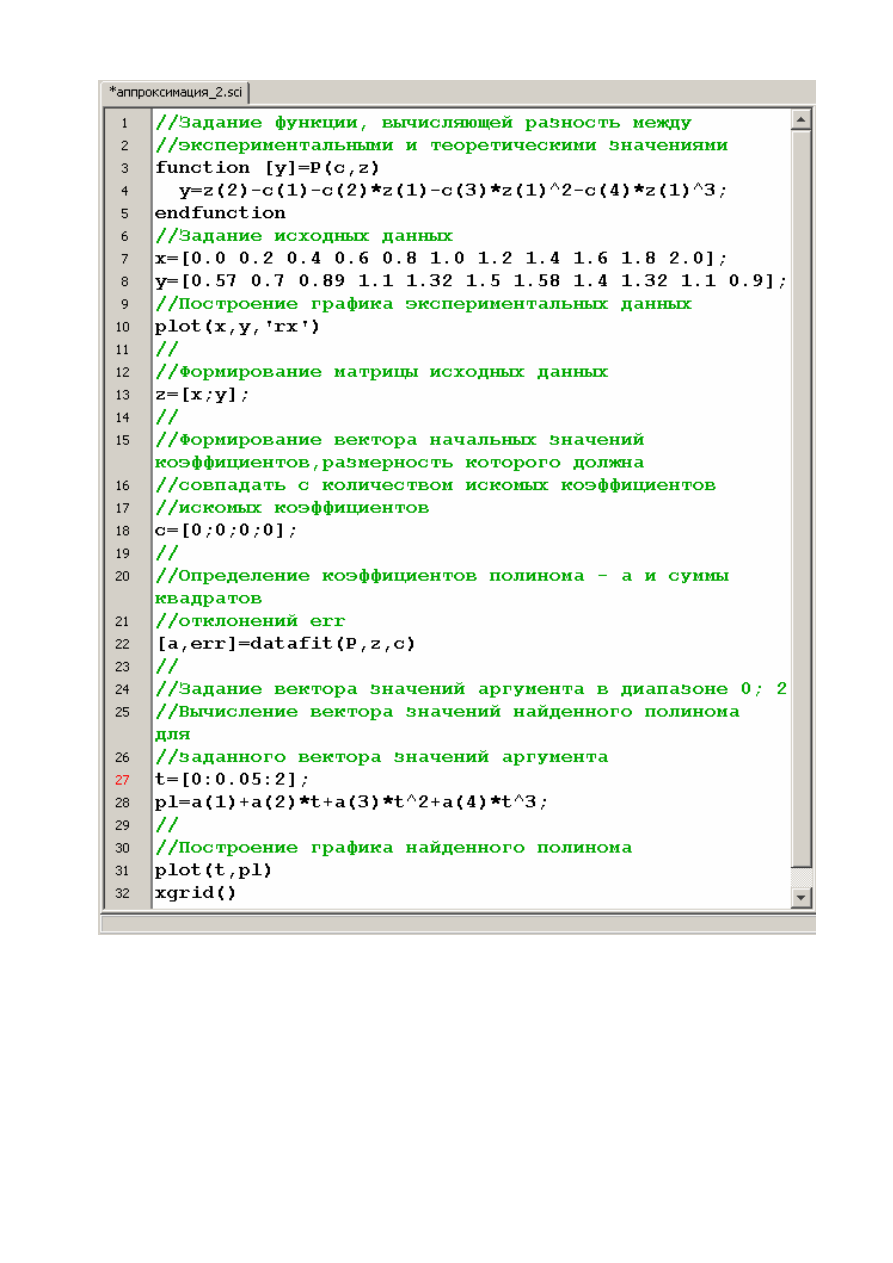
На рис. 25 приведен файл-сценарий подбора аппроксимирующего полинома с
помощью функции datafit.
48
Рис. 25. Файл-сценарий аппроксимации экспериментальных данных
полиномом 3 степени
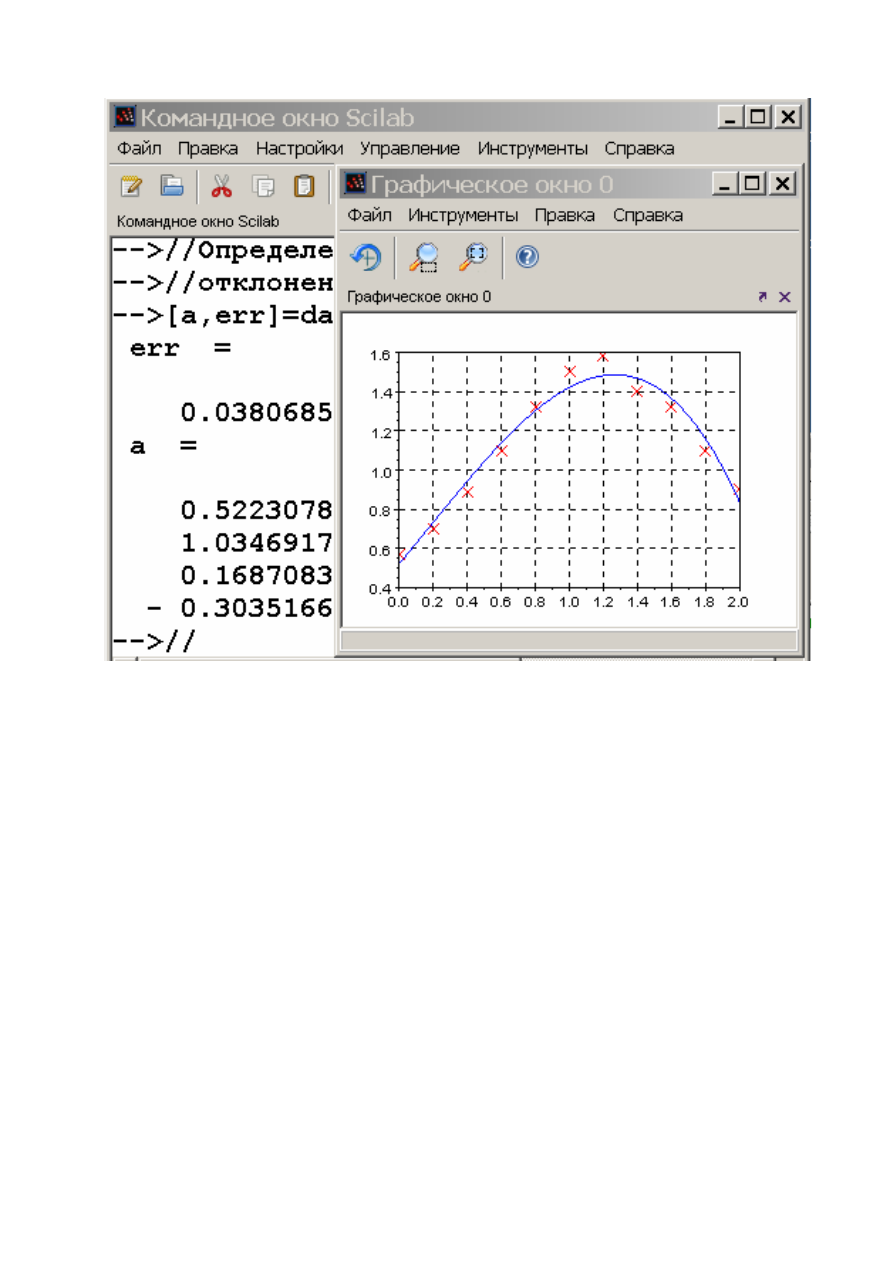
В результате работы функции datafit была подобрана аналитическая
зависимость в виде полинома
P
= −0,3x3 + 0,17x2 + 1,03x + 0,52 ,
а сумма квадратов отклонений измеренных значений от расчетных составила
0,038 (рис. 26).
49
Рис. 26. Решение задачи аппроксимации
Контрольные вопросы
1.
Квадратурные формулы прямоугольников (с оценкой точности).
2.
Квадратурная формула трапеций (с оценкой точности).
3.
Квадратурная формула Симпсона (с оценкой точности).
4.
Квадратурные формулы гауссова типа.
Лабораторная работа №4
Тема: Решение обыкновенных дифференциальных уравнений.
1.
Цель работы
Использование методов решения обыкновенных дифференциальных уравнений
для решения конкретных задач строительства.
2.
Учебные вопросы, подлежащие рассмотрению:
Решение дифференциального уравнения:
методом Коши,
методом Эйлера,
Методом Эйлера-Коши,
Рунге-Кутта 4-го порядка
Адамса.
3.
Порядок выполнения работы
Задание

50
Решить задачу Коши для дифференциального уравнения y=f(x,y) на отрезке
[a,b
] при заданном начальном условии и шаге интегрирования h.
Номер варианта соответствует порядковому номеру в списке.
Исполнение: С помощью инструментальных пакетов MS Office методами
Эйлера, Рунге-Кутта 4-го порядка и Адамса, предусмотрев вывод полученных
решений в виде таблиц и графиков.
Оценка: Сопоставление полученных результатов, решаемых различными
методами
Методические указания
Дана система дифференциальных уравнений:
Рассмотрим задачу Коши для данной системы. Пусть известны начальные
условия при x
0
= a: y
1
(x
0
) = y
10
, y
2
(x
0
) = y
20
, …, y
n
(x
0
) = y
n0
. Требуется найти y
1
(x),
y
2
(x),…, y
n
(x),
проходящие через заданные точки: (x
0
,y
10
), (x
0
,y
20
), …, (x
0
,y
n0
).
Методы решения одного дифференциального уравнения можно обобщить и на
их системы.
Метод Рунге-Кутта 4-го порядка для системы ОДУ 1-го порядка
Расчетные формулы метода Рунге-Кутта 4-го порядка для системы ОДУ 1-го
порядка: