Файл: методичка моя.docx

Возведение в степень

Для возведения в степень используют функцию СТЕПЕНЬ.

Синтаксис функции

СТЕПЕНЬ(А;В),

где

А - число, возводимое в степень;

В - показатель степени, в которую возводится число.

Отрицательные числа можно возводить только в степень, значение которой является целым числом. В остальном ограничений на возведение в степень нет.

Для извлечения квадратного корня можно использовать функцию КОРЕНЬ.

Синтаксис функции

КОРЕНЬ(А),

где

А - число, из которого извлекают квадратный корень.

Нельзя извлекать корень из отрицательных чисел.

Тригонометрические вычисления

В Microsoft Excel можно выполнять как прямые, так и обратные тригонометрические вычисления, то есть, зная значение угла, находить значения тригонометрических функций или, зная значение функции, находить значение угла.

Синтаксис всех прямых тригонометрических функций одинаков. Например, синтаксис функции SIN

SIN(А),

где

А - угол в радианах, для которого определяется синус.

Точно так же одинаков и синтаксис всех обратных тригонометрических функций. Например, синтаксис функции АSIN

АSIN(А),

где

А - число, равное синусу определяемого угла.

Следует обратить внимание, что все тригонометрические вычисления производятся для углов, измеряемых в радианах. Для перевода в более привычные градусы следует использовать функции преобразования (ГРАДУСЫ, РАДИАНЫ) или самостоятельно переводить значения, используя функцию ПИ().

Функция ПИ() вставляет значение числа (пи). Аргументов функция не имеет, но скобки после названия удалять нельзя.

Например, при необходимости рассчитать значение синуса угла, указанного в градусах, необходимо его умножить на ПИ()/180.

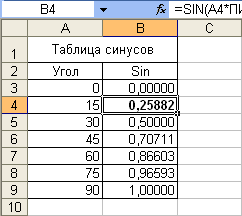Рис.5.  Вычисление тригонометрических функций для углов, указанных в градусах

Преобразование чисел

Преобразование чисел может потребоваться при переводе углов из градусов в радианы и обратно, при определении абсолютной величины числа, при преобразовании арабских цифр в римские.

Для перевода значения угла, указанного в радианах, в градусы используют функцию ГРАДУСЫ.

Синтаксис функции

ГРАДУСЫ(А),

где

А - угол в радианах, преобразуемый в градусы.

Для перевода значения угла, указанного в градусах, в радианы используют функцию РАДИАНЫ.

Синтаксис функции

РАДИАНЫ(А),

где

А - угол в градусах, преобразуемый в радианы.

Функции ГРАДУСЫ и РАДИАНЫ удобно использовать с тригонометрическими функциями. Например, при необходимости можно рассчитать значение синуса угла, указанного в градусах (рис. 6).

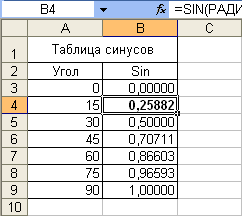Рис. 6.  Вычисление тригонометрических функций с использованием функций "ГРАДУСЫ" и "РАДИАНЫ"

Комбинаторика

Для расчета числа возможных комбинаций (групп) из заданного числа элементов используют функцию ЧИСЛКОМБ.

Синтаксис функции

ЧИСЛКОМБ(А; В),

где

А - число элементов;

В - число объектов в каждой комбинации.

Во вспомогательных расчетах в комбинаторике может потребоваться расчет факториала числа. Факториал числа - это произведение всех чисел от 1 до числа, для которого определяется факториал. Например, факториал числа 6 (6!) равен 1*2*3*4*5*6. Для расчета факториала используют функцию ФАКТР.

Синтаксис функции

ФАКТР(А),

где

А - число, для которого рассчитывается факториал.

Факториал нельзя рассчитать для отрицательных чисел. Факториал числа 0 (ноль) равен 1. При расчете факториала дробных чисел десятичные дроби отбрасываются.

Генератор случайных чисел

В некоторых случаях на листе необходимо иметь число, которое автоматически и независимо от пользователя может принимать различные случайные значения.

Для создания такого числа используют функцию СЛЧИС(). Функция вставляет число, большее или равное 0 и меньшее 1. Новое случайное число вставляется при каждом вычислении в книге. Аргументов функция не имеет, но скобки после названия удалять нельзя.

Статистические вычисления Расчет средних значений

В самом простом случае для расчета среднего арифметического значения используют функцию СРЗНАЧ.

Синтаксис функции

СРЗНАЧ(А),

где

А - список от 1 до 30 элементов, среднее значение которых требуется найти. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.

Нахождение крайних значений

Для нахождения крайних (наибольшего или наименьшего) значений во множестве данных используют функции МАКС и МИН.

Синтаксис функции МАКС:

МАКС(А),

где

А - список от 1 до 30 элементов, среди которых требуется найти наибольшее значение. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.

Функция МИН имеет такой же синтаксис, что и функция МАКС.

Функции МАКС и МИН только определяют крайние значения, но не показывают, в какой ячейке эти значения находятся.

Например, для данных таблицы на рис. 10 максимальное значение составит 13 % (ячейка Е1), а минимальное - 1 % (ячейка Е2).

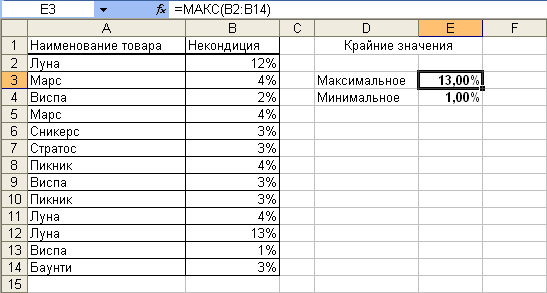Рис. 7.  Нахождение крайних значений с использованием функций "МАКС" и "МИН"

Расчет количества ячеек

Для определения количества ячеек, содержащих числовые значения, можно использовать функцию СЧЕТ.

Синтаксис функции:

СЧЕТ(А),

где

А - список от 1 до 30 элементов, среди которых требуется определить количество ячеек, содержащих числовые значения. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.

Например, в таблице на рис. 8 числовые значения в диапазоне А1:В17 содержат 12 ячеек.

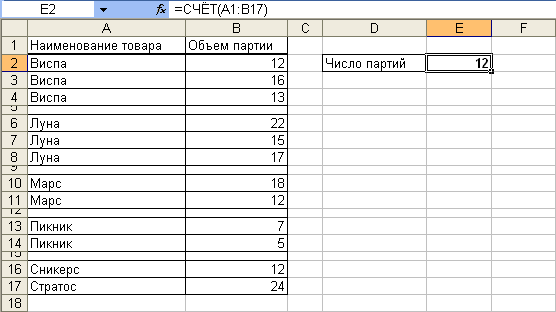Рис.8.  Расчет количества ячеек, содержащих числа, с использованием функции "СЧЕТ"

Если требуется определить количество ячеек, содержащих любые значения (числовые, текстовые, логические), то следует использовать функцию СЧЕТЗ.

Синтаксис функции:

СЧЕТЗ(А),

где

А - список от 1 до 30 элементов, среди которых требуется определить количество ячеек, содержащих любые значения. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки игнорируются.

Практическая часть

Задание 1. Создать и заполнить таблицу алгебраических функций, показанную на рисунке.

Алгоритм выполнения задания.

1. В ячейках А1:Н1 записать шапочки таблицы с предварительным форматированием ячеек, для этого:

1. Выделить диапазон ячеек А1:Н1.

2. Выполнить команду Формат Ячеек вкладка Выравнивание.

3. Установит переключатель «переносит по словам».

4. В поле «по горизонтали» выбрать «по центру».

5. В поле «по вертикали» выбрать «по центру».

6. Набрать тексты шапочек, подбирая по необходимости ширину столбцов вручную.

2. Записать в графу Число ряд чисел, начиная с 0:

1. В ячейки А2 и А3 записать 0 и 1.

2. Выполнить операцию Автозаполнение до числа 15.

3. Заполнить графу Десятичный логарифм следующим образом:

9. Выделить ячейку В2, вызвать Мастер функций, выбрать категорию математические, выбрать функцию LOG10.

10. В поле Число ввести адрес А2 с клавиатуры или, отодвинув диалоговое окно функции за любое место серого поля, щелкнуть ячейку А2.

11. Выполнить операцию Автозаполнение для всего столбца.

Примечание. В ячейке В2 должно быть #ЧИСЛО!, т. к. логарифм 0 не существует.

4. Заполнить графу Натуральный логарифм аналогично, выбрав функцию LN.

5. Заполнить графу Корень аналогично, выбрав функцию КОРЕНЬ.

6. Графы Квадрат и Куб заполнить следующим образом:

1. Выбрать функцию СТЕПЕНЬ.

2. В поле Число ввести адрес А2.

3. В поле Степень ввести 2 для квадратичной функции или 3 для кубической.

7. Заполнить графу Показательная функция следующим образом:

1. Выбрать функцию СТЕПЕНЬ.

2. В поле Число ввести 2.

3. В поле степень ввести адрес А2.

8. Заполнить графу Факториал аналогично пю3, выбрав функцию ФАКТР.

Примечание. Любую функцию можно записать с клавиатуры, точно соблюдая текст названия функции и её синтаксис, применяемый в Мастере функций.

Задание 2. Создать и заполнить таблицу тригонометрических функций, показанную на рисунке.

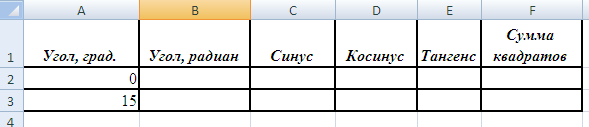
1. Заполнить графу Угол, град. числами от 0 до 180, используя операцию Автозаполнение.

2. Заполнить графу Угол, радиан значениями, применив функцию РАДИАНЫ.

3. Заполнить графы Синус, Косинус, Тангенс, применяя функции SIN, COS, TAN. В качестве аргумента выбирать значения угла в радианах.

Примечание. В некоторых ячейках значения записываются в экспоненциальной форме, например, запись 1,23Е-16 означает, что число 1, 23 возводится в степень минус 16, что даёт число, очень близкое к нулю, а запись 1,23Е+16 означает возведение числа 1,23 в степень плюс 16.

4. Заполнить графу Сумма квадратов известной формулой SIN²()+ COS²()=1, проверить результат для всех углов.

Задание 3. Создать и заполнить таблицу расчёта доходов, показанную на рисунке.

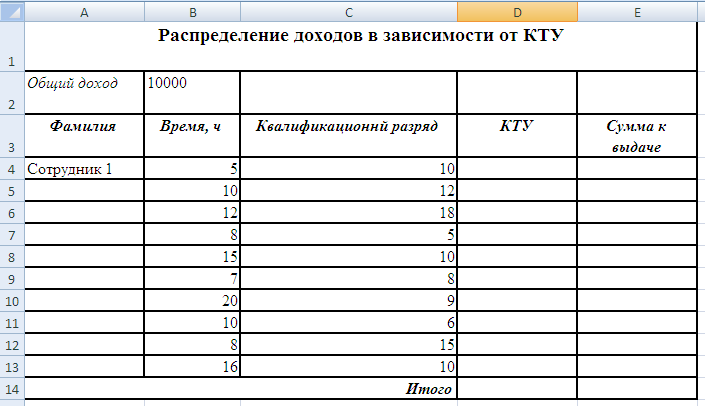
Алгоритм выполнения задания.

1. Записать исходные значения таблицы, указанные на рисунке.

2. Заполнить графу Фамилия значениями Сотрудник 1÷10, используя операцию Автозаполнение.

3. Рассчитать графу КТУ как произведение времени, затраченного сотрудником, на его квалификационный разряд (формула =В4*С4).

4. Подсчитать значение Итого с помощью операции Автосумма.

5. Графа Сумма к выдаче рассчитывается как произведение общего дохода на отношение КТУ данного сотрудника к итоговому КТУ (формула =В2*D4/D14).

6. При выполнении операции Автозаполнение в графе Сумма к выдаче появляются ошибки #ЗНАЧ! и #ДЕЛ/0!. Это происходит из-зи того, что при применении формулы происходит изменение адресов в ней, например, в ячейке Е5 формула содержит адреса = В3*D5/D15.

7. Для правильного расчёта необходимо зафиксировать адреса В2 и D14, для этого:

   1. Выделить ячейку Е4.