ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.06.2024
Просмотров: 559
Скачиваний: 0
СОДЕРЖАНИЕ
Более элементарные по сравнению с атоллами
Осколки частиц, или Трудное разделение
Физика возвращается к повседневным заботам
Теория наносит ответный удар: объединение
Теневая сторона стандартной модели
Проблема происхождения массы, известная как проблема полей Хиггса
Решение головоломки: как, кто, где и когда?
Предположения о происхождении жизни
Нынешняя жизнь: клеточные структуры
Решение головоломки: как, кто и почему?
Секвенирование генома человека
Решение головоломки: почему, как, кто и где, когда?
Получение или утрата атмосферного газа
Погода и климат: гипотезы (весьма добротные), прогнозы (не столь добротные)
Решение головоломки: как и где?
Измерение межзвездных расстояний
Галактики: первые теории и наблюдения
Космологический вклад Эйнштейна
Чем крупнее телескопы, тем больше расстояния до звезд
Одна большая Галактика или многочисленные обособленные галактики
Столкнувшись с неожиданным: ускорение Вселенной
В темноте рассуждать о темной энергии
Решение головоломки: где, когда, как и кто?
2. Какова доля таких звезд, имеющих планеты ?
3. Какова доля планет, обращающихся вокруг своих звезд в пределах, где возможно зарождение жизни ?
4. Какова доля благоприятно расположенных планет, где действительно зародилась жизнь?
5. Какова доля форм жизни, приведших к возникновению разума ?
7. В течение скольких лет разумная цивилизация передает в космос поддающиеся обнаружению сигналы?
13 .Предсказание землетрясений
15. Труды Эйнштейна: помимо теории относительности
Глава 2. Физика. Почему одни частицы обладают массой, а другие нет?
Глава 3. Химия. Какого рода химические реакции подтолкнули атомы к образованию первых живых существ?
Глава 4. Биология. Каково строение и предназначение протеома?
Глава 5. Геология. Возможен ли точный долговременный прогноз погоды?
Глава 6. Астрономия. Почему Вселенная расширяется со все большей скоростью?
Погода и климат: гипотезы (весьма добротные), прогнозы (не столь добротные)
Получив для наблюдения столь замечательное собрание атмосферных газов на Земле, наука готовилась создать предполагаемую модель долгосрочного (климат) и краткосрочного (погода) поведения атмосферы. Благодаря усилиям Исаака Ньютона в 1660-е годы удалось описать движение тел в виде ряда общих и действенных уравнений. И в последующие два века, XVIII и XIX, наука распространила представления Ньютона на случаи больших, малых тел, жидкостей и газов.
Одним из достоинств ньютоновых законов стало то, что, зная заданные для определенного времени условия, можно вычислить последующее движение. С философской точки зрения это детерминизм. Мощь данного метода огромна. Возможен точный расчет положения планет, предсказание приливов и отливов на много лет вперед и построение траектории полета снарядов. К тому же подобные предсказания можно обратить вспять, что позволяет изучать не только будущее, но и прошлое.
Одно из следствий детерминизма состоит в том, что будущее поведение системы легко предугадать, определяя состояние системы в какой-то предшествующий момент. Это предыдущее состояние именуют начальными условиями. На рис. 5.3 подобный процесс представлен в упрощенном виде; с помощью графика можно описывать дальность полета снаряда в зависимости от угла возвышения. При изменении угла в пределах нескольких градусов дальность колеблется в весьма существенных границах. Для получения большей точности попадания разброс угла возвышения необходимо уменьшить.
По существу, результаты с требуемой точностью получаются заданием начальных условий с соответствующей точностью. Неявно в измерениях по проверке прогноза присутствует допущение, что увеличение точности измерений улучшит точность предсказанных результатов.
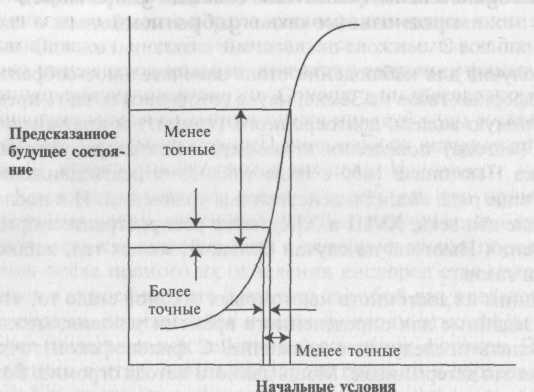
Рис. 5,3. Точность предсказания будущего состояния зависит от точности знания начальных условий
И хотя на протяжении долгого времени такое допущение считалось незыблемым, на исходе XIX века вера в него была поколеблена при весьма странном стечении обстоятельств.
В 1887 году шведский король Оскар II [(1829-1907), король Швеции в 1872—1907 годах и Норвегии в 1872—1905 годах] в ознаменование своего 60-летия пообещал денежную премию тому, кто математически докажет устойчивость орбит планет Солнечной системы. Победитель, Жюль-Анри Пуанкаре, не решил полностью поставленной задачи, но проделанной работы хватило для получения премии. В 1889 году он опубликовал статью «О задаче трех тел и об уравнениях динамики» (Acta Mathematica. 1890. № 13)16. Пуанкаре столкнулся с необычным положением, когда «небольшие расхождения в начальных условиях ведут к огромным различиям у наблюдаемых в итоге явлений».
Будучи выдающимся математиком, он сумел показать, что при достижении системой определенной степени сложности получение точных результатов потребует предельно точных начальных условий. Некоторое время соображения Пуанкаре казались математическим курьезом. Но, как мы вскоре увидим, спустя 70 лет они дадут знать о себе.
Пока же вернемся к прогнозу погоды. Любопытное событие произошло во время Первой мировой войны. Льюис Фрай Ричардсон работал в различных научных учреждениях, включая Метеорологическую службу Британии. С началом войны он смог найти себе применение, не поступаясь своими пацифистскими убеждениями: водил санитарную машину во Франции. В часы досуга он строил математическую модель предсказания погоды, основанную на разделении земной поверхности на ячейки, получении данных о погоде в каждой из них и последующем прогнозе погоды посредством математического приема, известного как исчисление конечных разностей. Его модель так и не заработала, но он представил в 1922 году используемый им математический прием в ставшей знаменитой книге «Предсказание погоды с помощью численного процесса». Ричардсон отнес неудачу модели на счет недостаточного количества данных и трудностей ведения громоздких вычислений вручную17.
Вскоре обычные вычисления препоручили ЭВМ. К 1953 году обосновавшийся в Принстоне венгерский математик Джон фон Нейман успел испробовать первую цифровую вычислительную машину ЭНИАК (ENIAC — Electronic Numerical Integrator and Computer) Принстонского университета на многих задачах, включая уравнения Ричардсона. Хотя машинные расчеты и позволяли делать сравнительно неплохой прогноз погоды, работы оставалось еще непочатый край.
ЭВМ оказалась весьма полезным орудием. В 1960 году Эдуард Лоренц сумел «выбить» для себя новую ЭВМ [Royal МсВее]. Он изучал математику в Гарварде, а теперь преподавал метеорологию в Массачусетском технологическом институте. Для проверки машины Лоренц составил программу для 12 нелинейных уравнений, описывающих поток жидкости применительно к погоде. Эти уравнения включали воздействие давления, скорости ветра, температуры воздуха и влажности. По современным меркам ЭВМ Лоренца была весьма примитивной, но результаты выдавала вполне разумные.
Один прогон оказался столь любопытным, что Лоренц решил расширить его. Из-за медлительности тогдашних ЭВМ он начал прогон программы с середины, введя случайно взятое число 0,506 из распечатки. Затем Лоренц отправился пить кофе, а машина продолжала «перемалывать» содержимое. Вернувшись, он был поражен увиденным: часть нового прогона, перекрывающаяся со старым, содержала отличные от прежних результаты. Причем отличие было разительным. После кропотливой проверки Лоренц выяснил, что ЭВМ использовала числа с шестью знаками после запятой, но выдавала их округленными до трех знаков. Поэтому числу 0,506 на распечатке соответствовало машинное число 0,506127.
Но каким образом столь малая разница на входе могла привести к такому разительному расхождению на выходе? Эдуард Лоренц заново открыл явление, о котором говорил Пуанкаре. В своей статье 1963 года «Детерминированное непериодическое течение» [в кн.: Странные аттракторы. М., 1981] Лоренц указывает, насколько конечный результат чувствителен к начальным условиям.
На рис. 5.4 представлена кривая трехмерной функции, порождаемой нелинейными уравнениями данного рода. Хотя ее значения так и не сходятся к одной точке, они колеблются вокруг двух точек, словно притягивают к себе функцию, отсюда и название «странный притягиватель (аттрактор)».
Чтобы заострить внимание на том, как малые различия ведут к большим последствиям, а возможно, руководствуясь наглядным образом странного аттрактора, свое выступление [в декабре 1972 года перед Американским обществом содействия науке] Лоренц озаглавил так: «Вызовет ли взмах крыла бабочки в Бразилии смерч в Техасе?» Выражение «эффект бабочки» вскоре стало общепринятым. Системы уравнений с подобным поведением уже создавались и изучались независимо от возможности применять их к физическим системам.
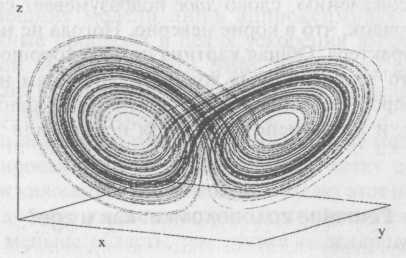
Рис. 5.4. Странный аттрактор
ХАОС: КУХНЯ

В итоге возникла совершенно новая отрасль математики с, пожалуй, вводящим в заблуждение названием «теория хаоса», придуманным математиком Джеймсом Йорком из Мэрилендского университета (см.: Список идей, 12. Теория хаоса). К сожалению, слово хаос подразумевает совершенный беспорядок, что в корне неверно. Погода не носит случайного характера. Общая картина погоды хорошо всем известна: лето теплое, а зима холодная. Чего нам недостает, так это подробностей: насколько теплой или холодной будет погода, и ждать непогоду спустя неделю или же ровно через час.
Решение головоломки: как и где?
Есть несколько мнений о путях достижения более точного, долгосрочного прогноза погоды.
КАК И ГДЕ Улучшение методов
Совершенствование наблюдений за погодой. Требуется больше данных и лучшего качества. Есть места на Земле, откуда поступает крайне мало данных, прежде всего это горные районы и океанические поверхности. Два больших сезонных течения поверхностных океанических вод, Эль-Ниньо и Ла-Нинья, вызывают обширные синоптические явления, существенно воздействующие на погоду в мире, особенно сказываясь на сельском хозяйстве. Точный долговременный прогноз помог бы крестьянам сохранить сотни миллионов долларов. В рамках проектов наподобие ARGO, составной части Системы наблюдения за климатом Земли, на океанических просторах размещаются 3 тыс. дрейфующих станций для слежения за погодными и водными условиями.
Повышение качества моделирования. Современное ма тематическое моделирование значительно совершен ней методов Эдуарда Лоренца, но многое еще пред стоит сделать. Некоторые физические процессы, управляющие погодой, весьма сложны. Нужно учитывать рельеф местности и свойства почвы, брать в расчет динамическое поведение океана и облачного покрова. Нынешние модели лишь аппроксимируют крайне сложные процессы в целях ускорения вычислений с учетом объемов памяти ЭВМ. К тому же различные службы придерживаются собственных моделей со своими аппроксимациями.
Уменьшение шага сетки у модели. Первые модели прогнозирования погоды использовали сетку с шагом в сотни километров. В нынешних моделях этот шаг уменьшен до десятков километров, а ближайшая цель — 5 км. Чем меньше область, тем точнее моделирование, однако для получения такой точности нужны суперЭВМ (вспомним потребность биологии в больших вычислительных мощностях, получившую название биоинформатики). В построении суперЭВМ наметилось два подхода: массовая параллельная обработка и векторные вычисления. Процессоры с массовым параллелизмом соединяют большое число универсальных процессоров, каждый из которых осуществляет часть сложного вычисления, а отдельные результаты суммируются. Векторная обработка использует специализированные микропроцессоры, предназначенные для решения сугубо определенной задачи. В свое время американский разработчик ЭВМ Сеймор Крей собирал необыкновенно быстрые суперЭВМ на основе векторного вычисления. Хотя его подход перестал пользоваться спросом на родине, к нему решила прибегнуть японская компания NEC. Вместо перехода на сетку с меньшим шагом для всего земного шара было решено, что качество прогноза у глобальных моделей можно улучшить при сетках с переменным шагом в особо важных областях.
Сборный прогноз. Сборный прогноз — метод, учитывающий чувствительность моделей к малым изменениям в начальных условиях. Данный подход связан с неоднократным прогоном модели, использованием различных начальных условий, чтобы посмотреть, как меняются выходные данные. Если, например, дождь выпадает в четырех испытаниях из десяти, можно прогнозировать 40% вероятности дождя. Обычно модели запускают более 10 раз — часто это 17 прогонов, но порой может быть и 46. Одна из разновидностей данного подхода связана со сравнением результатов различных моделей с последующим прогнозированием на основе средневзвешенного значения. Опытные метеорологи используют ЭВМ, когда сверяют результаты, и порой отклоняют выданный ею прогноз исходя из собственного опыта.
Признание невозможности подробного долгосрочного прогноза и изучение лишь общих тенденций
Как пишет популяризатор науки Джеймс Глейк в книге ХАОС: создание новой науки (1987) [СПб., 2001]:
Предположим, что Земля покрыта датчиками на удалении одного фута друг от друга, а по высоте — идущими на расстоянии одного фута вплоть до верхних слоев атмосферы. Предположим, что каждый датчик снимает совершенно точные показания температуры, давления, влажности и любой иной величины по желанию метеоролога. Ровно в полдень обладающая неограниченной мощностью ЭВМ получает все эти данные и вычисляет, что произойдет в каждой точке в 12.01, потом в 12.02 и т. д. И тем не менее ЭВМ не в состоянии предсказать, будет ли в Принстоне, штат Нью-Джерси, солнечно или пасмурно через месяц.
Устоявшаяся сеть прогнозирования погоды не приемлет невозможности прогнозирования. Пока не удастся делать более точные прогнозы на срок более двух недель, приходится мириться с возможностью исходной непредсказуемости погоды. В некотором отношении здесь улавливается сходство с другой задачей науки о Земле: прогнозированием землетрясений (см.: Список идей, 13. Предсказание землетрясений).
Выработка совершенно нового подхода
При всех любопытных свойствах, проявляемых теорией хаоса и теорией катастроф, занятой изучением скачкообразных перестроек систем как чистой математики, для извлечения научных выгод требуется их более тесное соотнесение с физической реальностью. Свежий подход на основе простых правил программирования [так называемой системы компьютерной алгебры] предложил в 2002 году Стивен Вольфрам. Его идеи могут помочь в прогнозе погоды и иных областях науки, однако потребуется еще много усилий для соотнесения его отвлеченных математических методов моделирования с реальным миром.