Файл: Методические указания по изучению дисциплины и выполнению контрольных работ для студентов заочной формы обучения направлений.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 131
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, получим 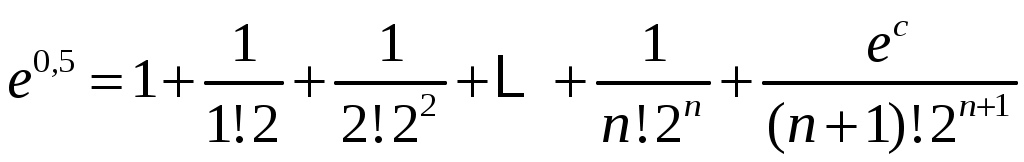 .
.
Определим число n так, чтобы погрешность приближенного равенства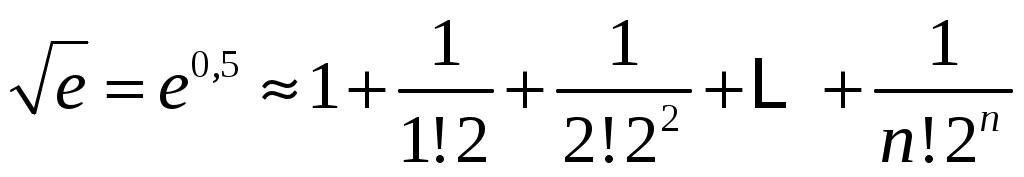 не превышала 0,0001. Погрешность этого равенства определяется остаточным членом, следующим после
не превышала 0,0001. Погрешность этого равенства определяется остаточным членом, следующим после 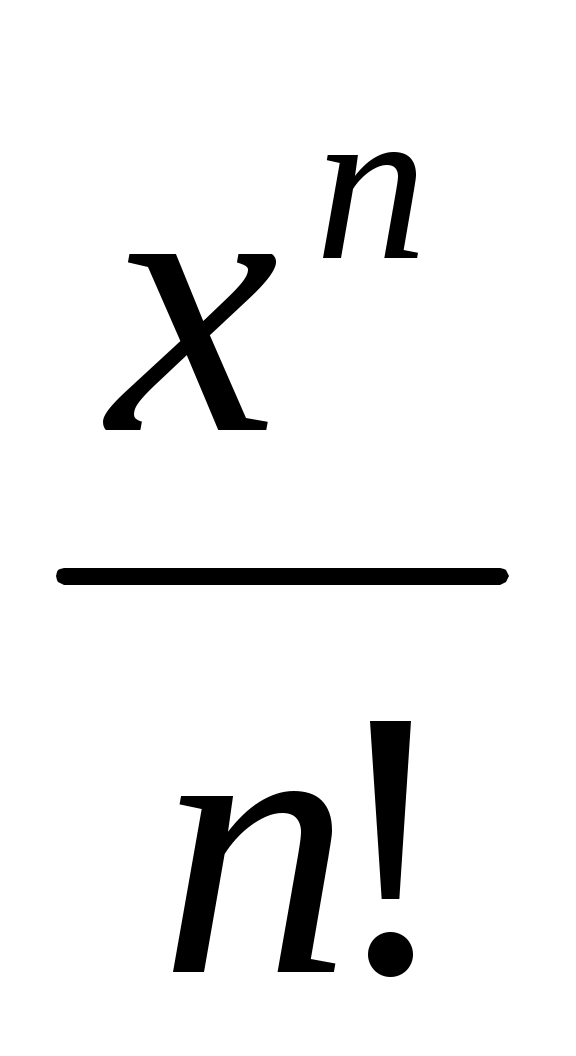 в разложении
в разложении 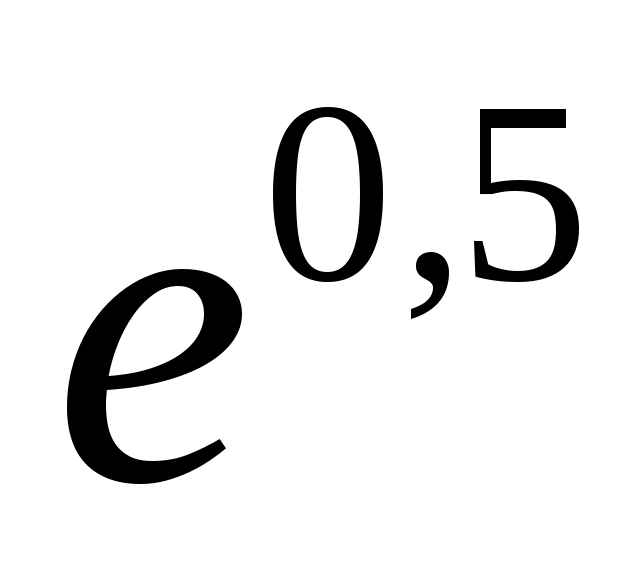 :
:  . Так как
. Так как 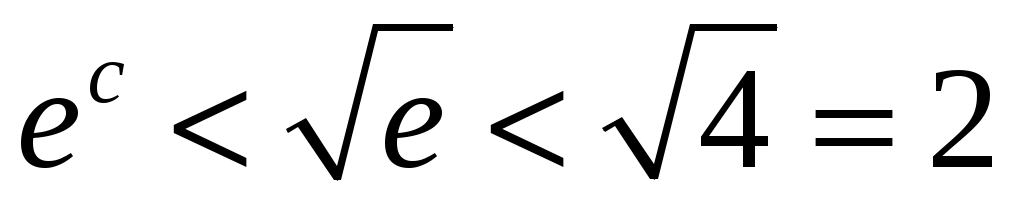 , то
, то 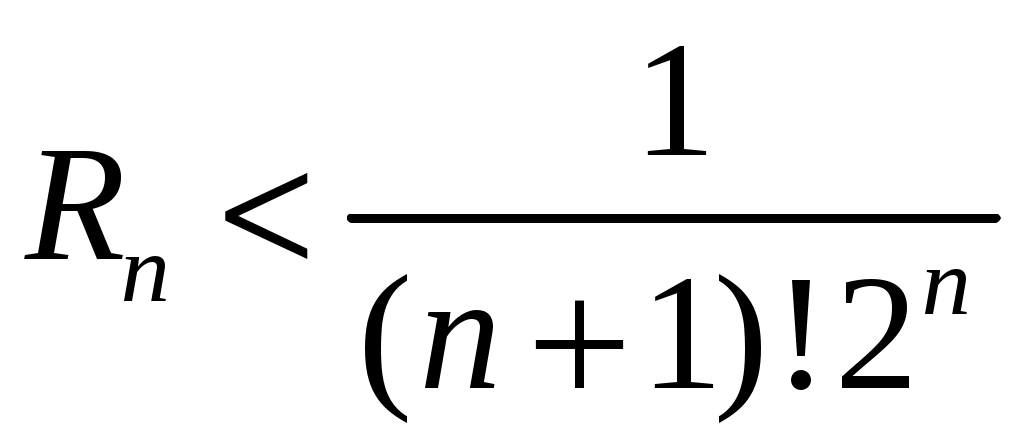 . Путем подбора найдём, при каком наименьшем n будет
. Путем подбора найдём, при каком наименьшем n будет  . Получаем, что
. Получаем, что 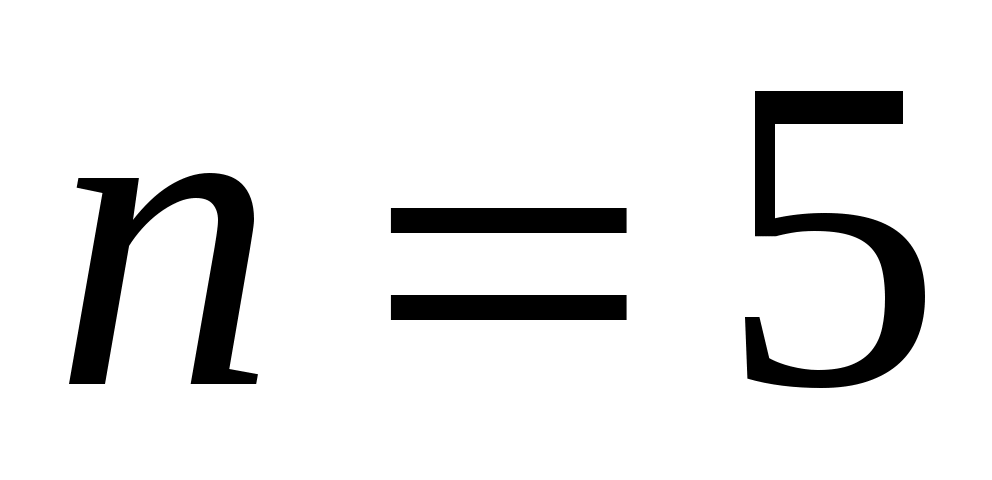 :
: 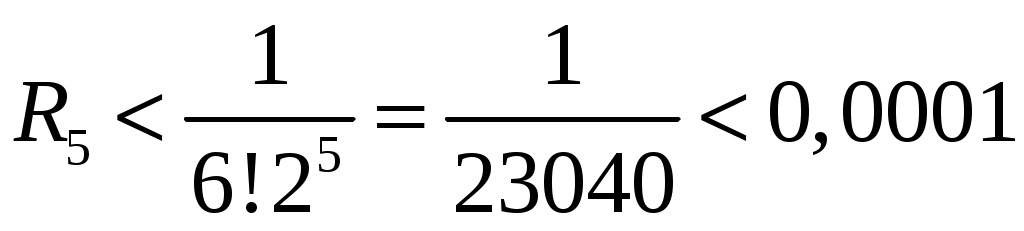 . Тогда
. Тогда 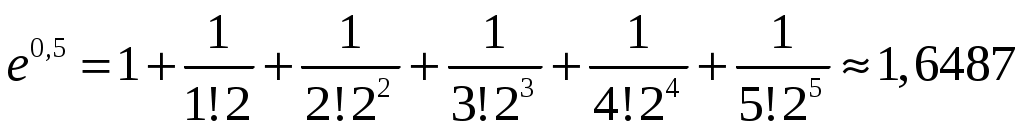 .
.
Задание №9. Общая схема исследования функции и построения графика.
1. Найти область определения функции.
2. Определить тип функции (четность, нечетность).
3. Найти точки пересечения с осями координат и интервалы знакопостоянства функции.
4. Найти асимптоты графика функции:
а) вертикальные; б) невертикальные (наклонные).
5. Найти точки возможного экстремума и интервалы возрастания и убывания функции.
6. Найти точки перегиба и интервалы выпуклости, вогнутости функции.
7. Найти дополнительные точки.
8. Построить график функции, учитывая проведенные исследования.
Пример. Исследовать функцию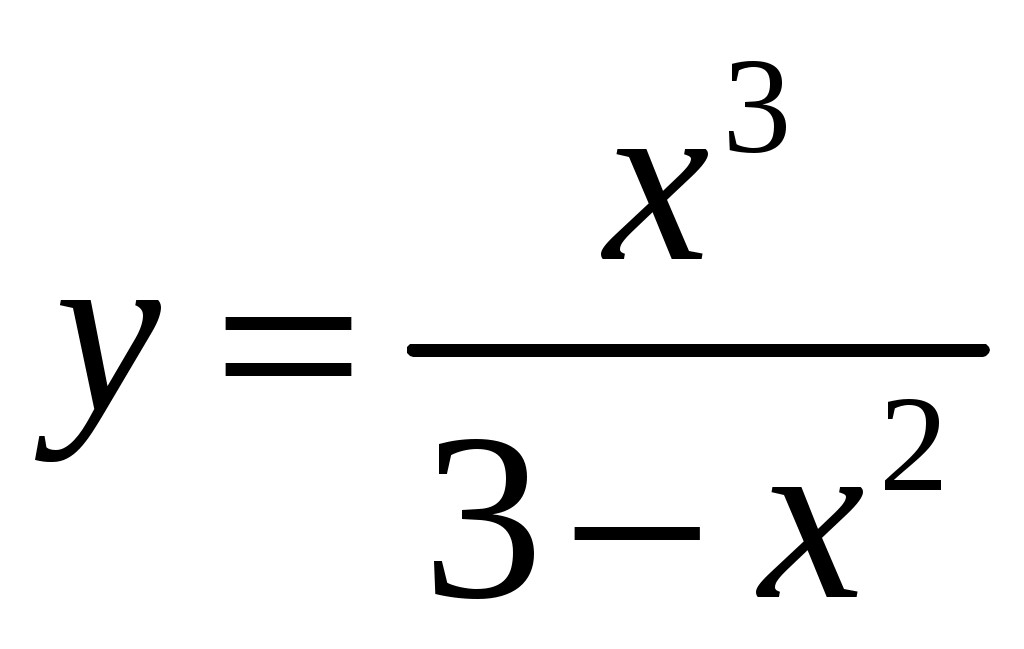 и построить ее график.
и построить ее график.
Решение
1. Функция определена на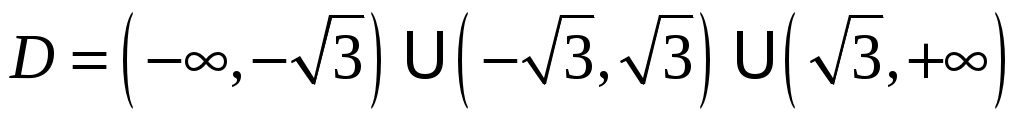 .
.
2. Так как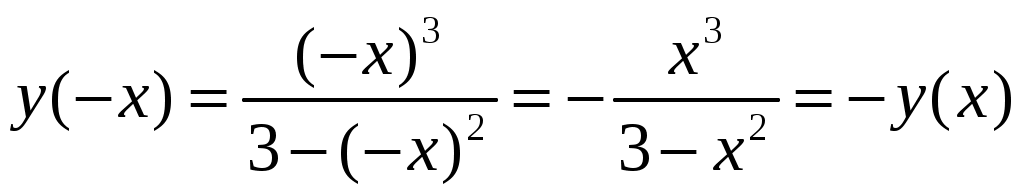 , то функция
, то функция 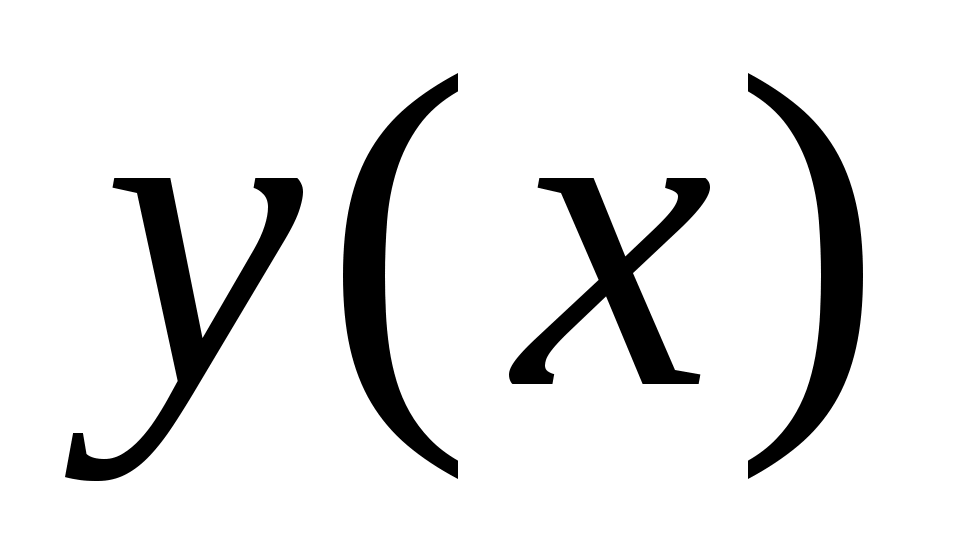
нечетная.
3.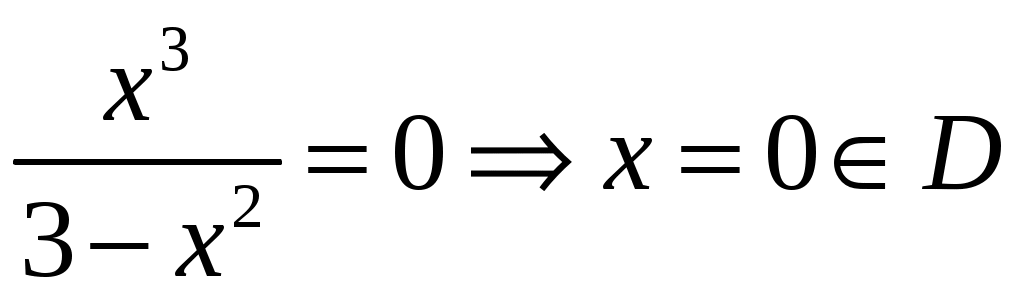 .
.
4. а) Вертикальные асимптоты:
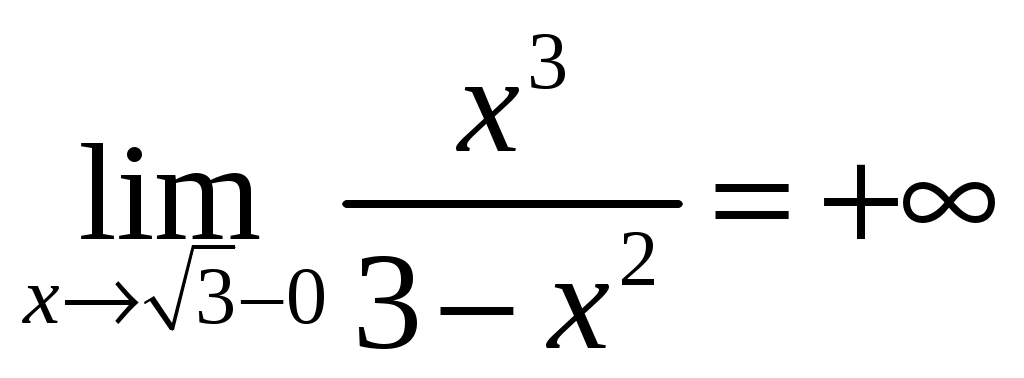 ;
; 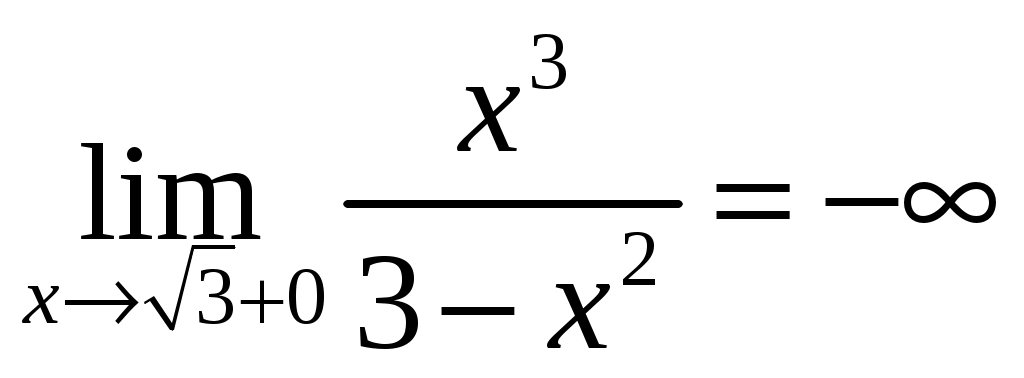 .
.
Следовательно,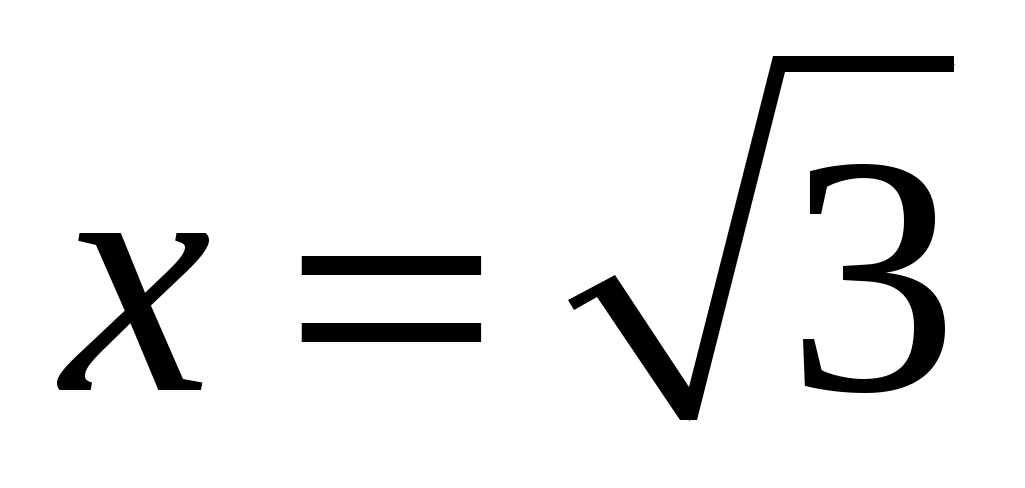 - точка разрыва второго рода. Так как функция
- точка разрыва второго рода. Так как функция  нечётная, то
нечётная, то 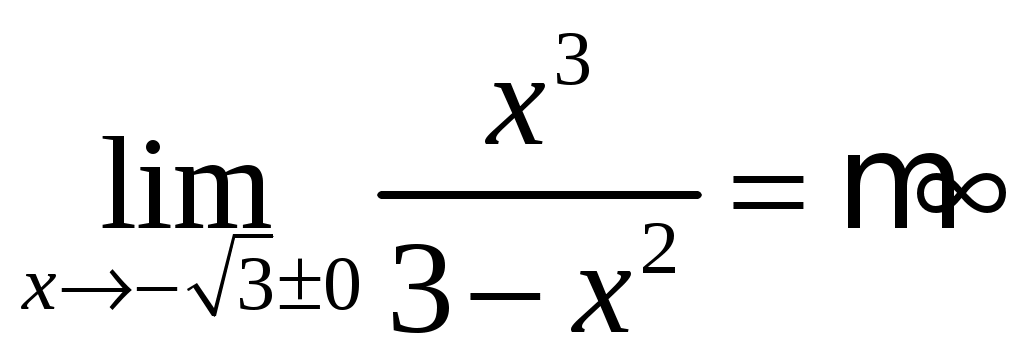 и
и 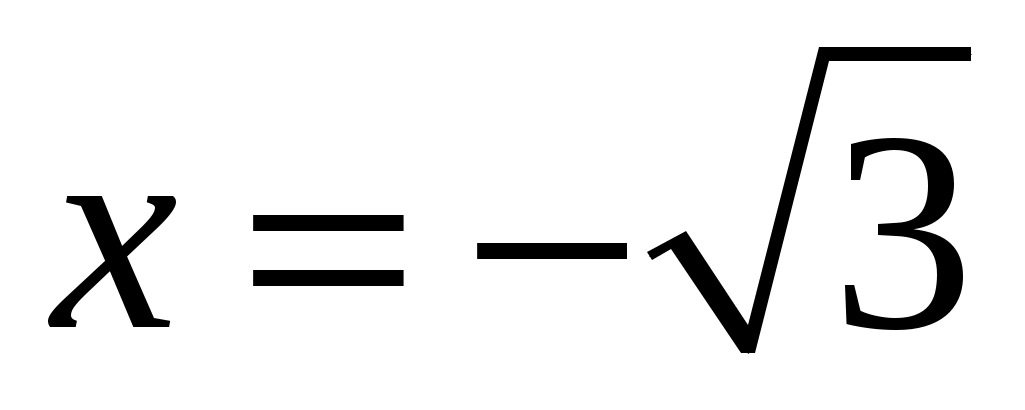 - точка разрыва второго рода. Тогда уравнения вертикальных асимптот будут
- точка разрыва второго рода. Тогда уравнения вертикальных асимптот будут 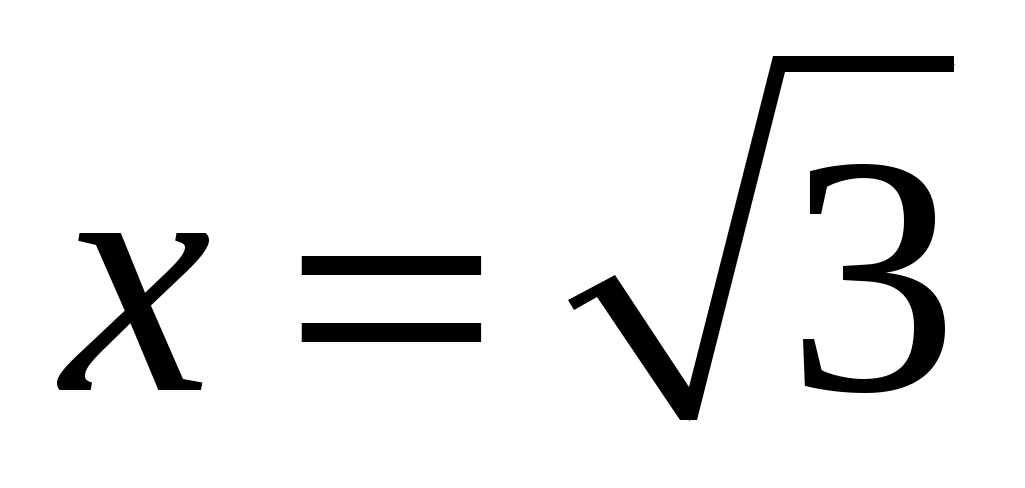 и
и 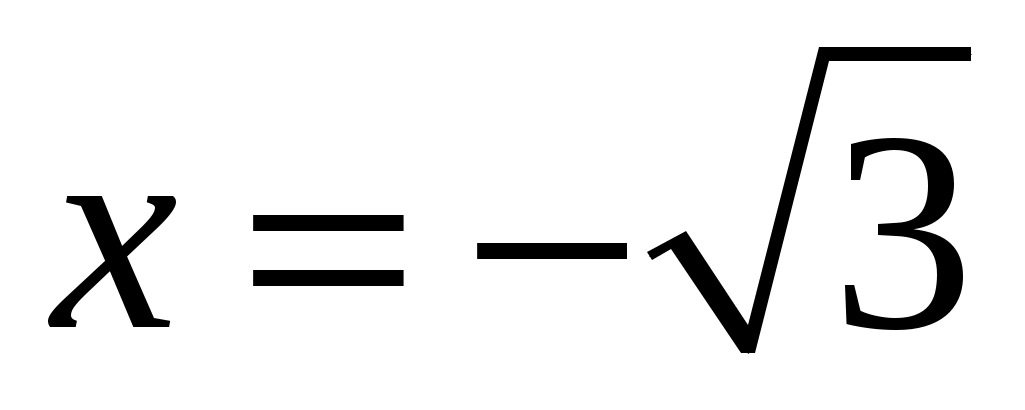 . Других вертикальных асимптот график функции
. Других вертикальных асимптот график функции  не имеет.
не имеет.
б) Наклонные асимптоты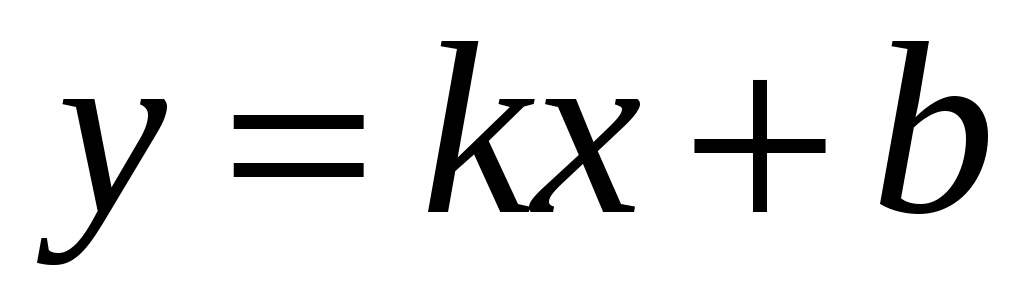 :
:
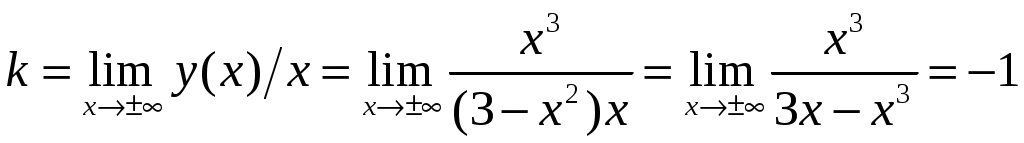 ;
;
 .
.
Итак,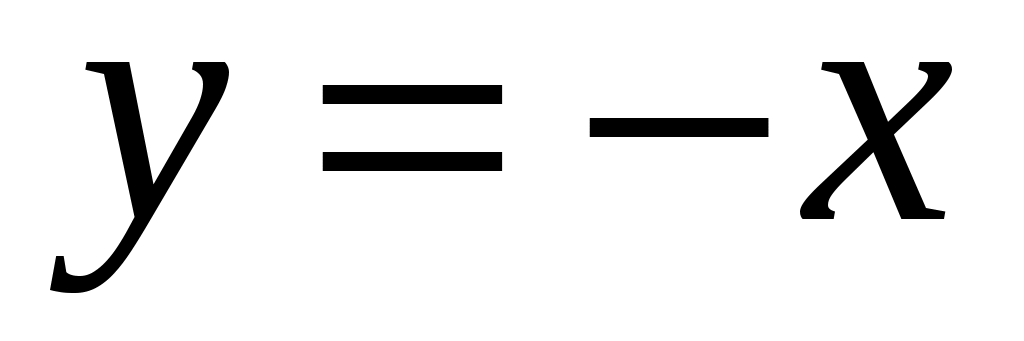 - уравнение наклонной асимптоты графика функции.
- уравнение наклонной асимптоты графика функции.
5. .
.
Из уравнения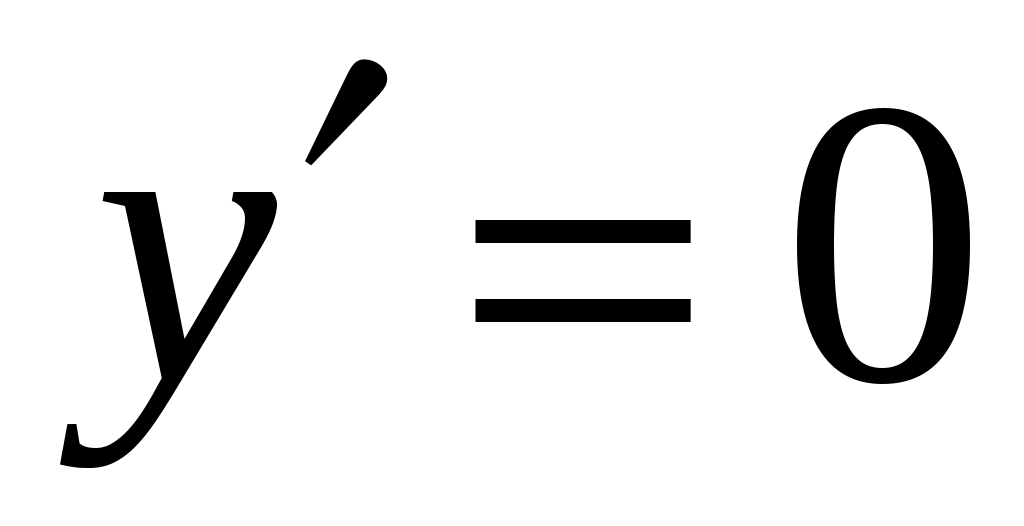 находим критические точки
находим критические точки 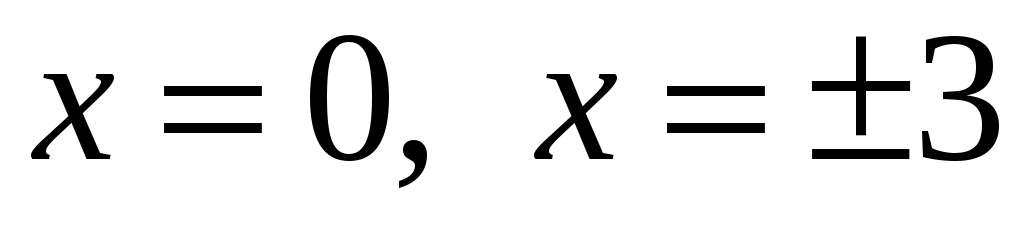 . Так как
. Так как  и
и 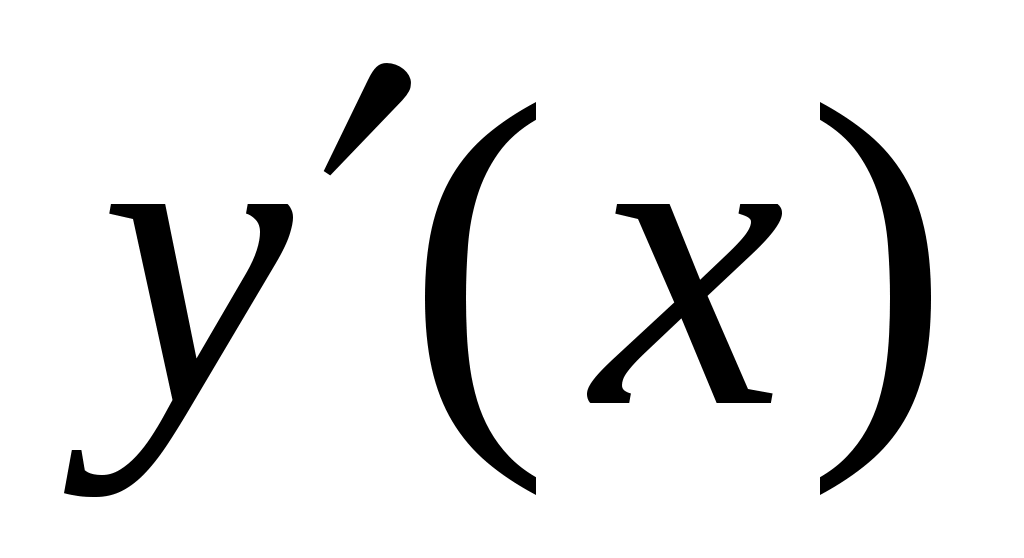 не существует при
не существует при 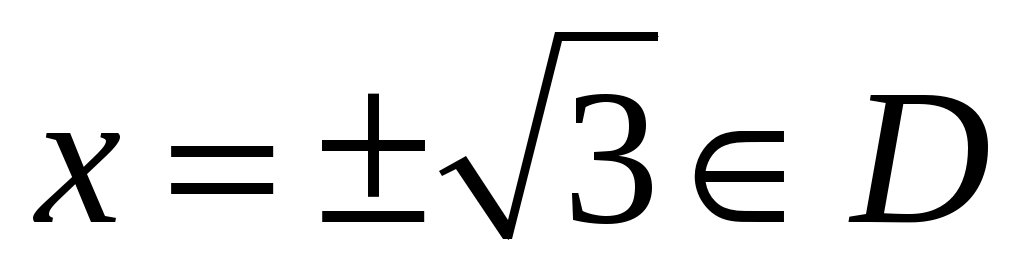 , то
, то 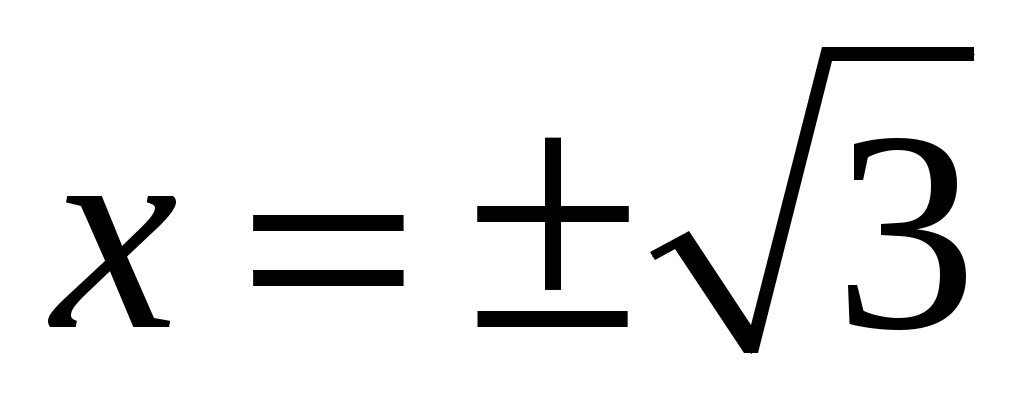 не являются критическими точками функции
не являются критическими точками функции  .
.
6.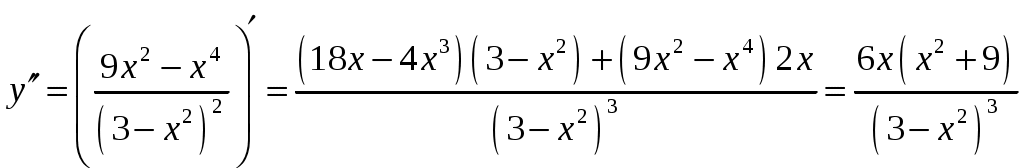 . Из уравнения
. Из уравнения 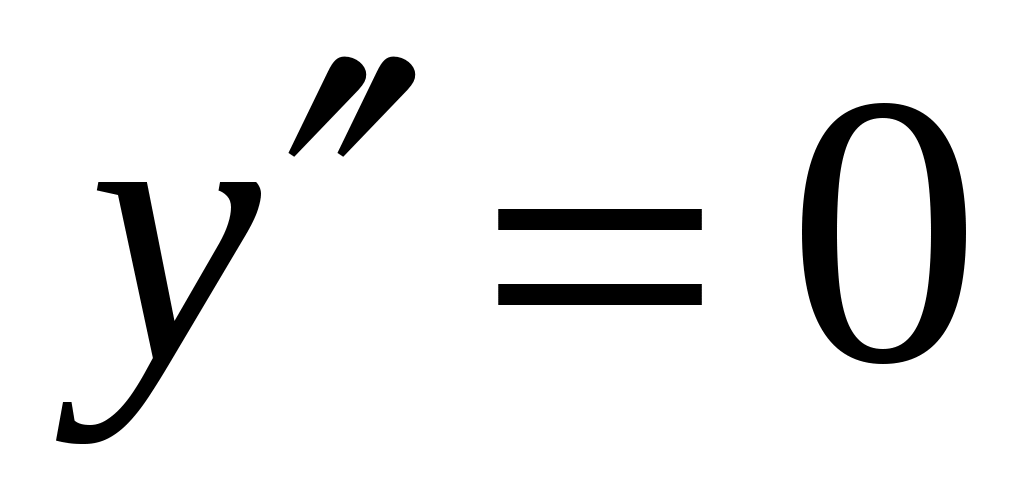 или
или 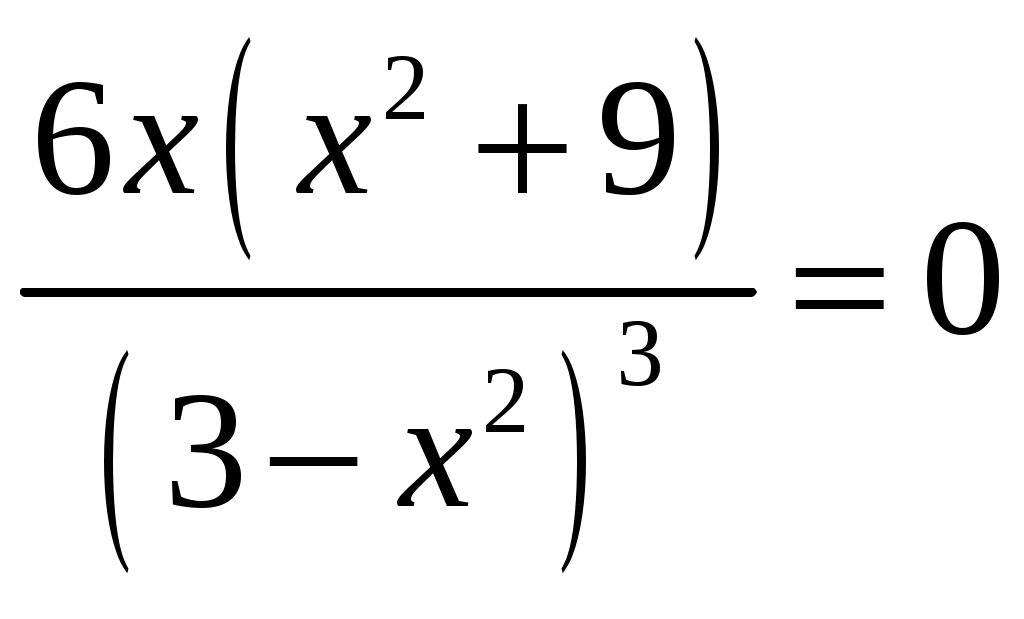 находим, что
находим, что 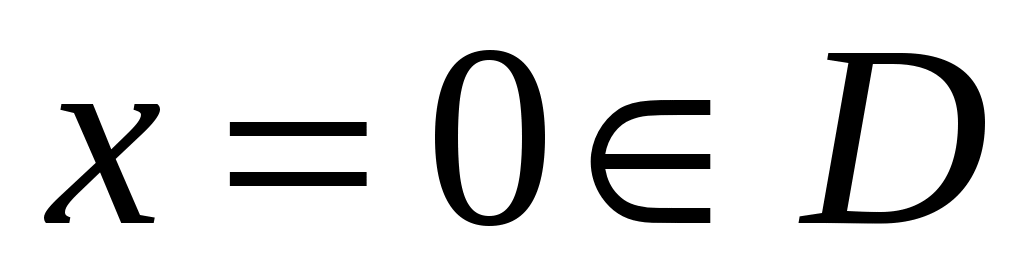 - критическая точка второго рода. Так как
- критическая точка второго рода. Так как  не существуют при
не существуют при 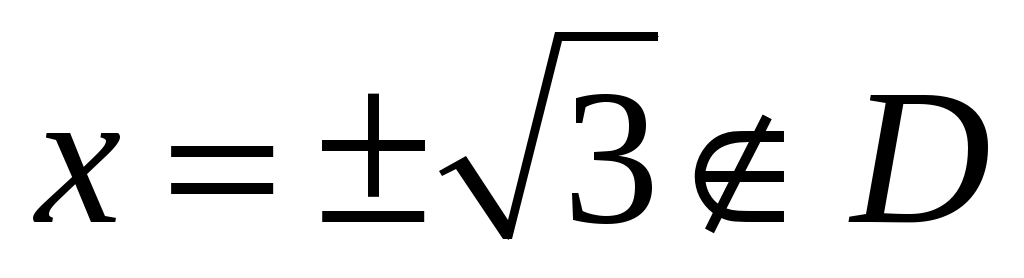 , то эта точки не являются критическими точками второго рода функции
, то эта точки не являются критическими точками второго рода функции  .
.
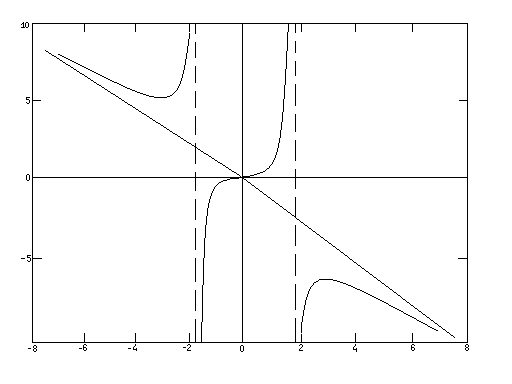
7.Строим график функции.
3.2 Контрольная работа № 2. Семестр 2
Программой дисциплины «Математика» для студентов 1 курса во втором семестре предусмотрено выполнение контрольной работы № 2.
При выполнении контрольной работы № 2 необходимо изучить основные понятия и определения функции нескольких переменных. Научится вычислять частные производные. Научиться вычислять двойные интегралы через повторные. Изучить теорию числовых рядов. Необходимо знать основные признаки сходимости числовых рядов. Уметь вычислять радиус сходимости и, пользуясь им, интервал сходимости степенного ряда. Изучить теорию дифференциальных уравнений и научиться находить решения дифференциальных уравнений в простейших случаях. Изучить основные понятия теории вероятности: алгебру случайных событий, вероятность случайного события, условную вероятность случайного события, независимость двух случайных событий. Изучить основные понятия, связанные со случайными величинами. Уметь вычислять по известному закону распределения математическое ожидание и дисперсию.
Ниже приведены примеры выполнения заданий.
Задание № 1. Найти неопределенные интегралы, правильность результаты проверить дифференцированием.
Пример. Найти неопределенные интегралы.
а) . Применим подстановку
. Применим подстановку 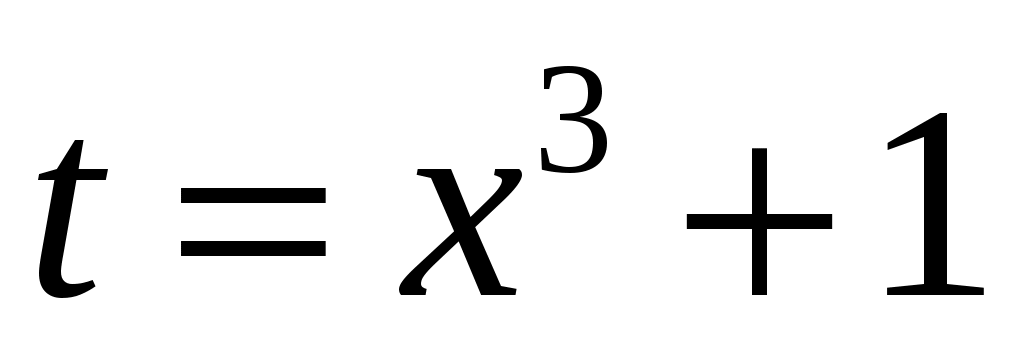 . Тогда
. Тогда 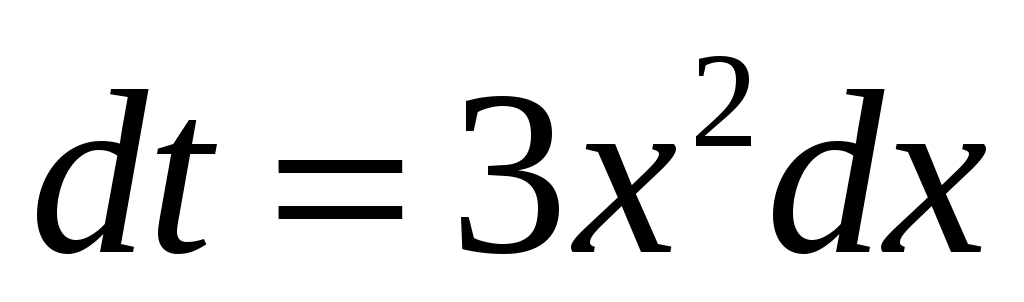 . Откуда
. Откуда 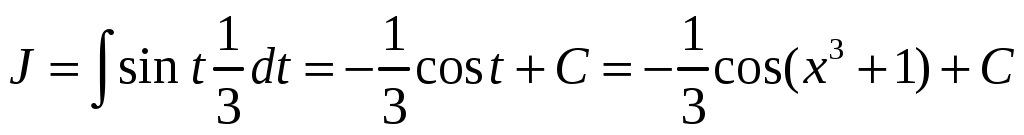 . Проверим этот результат дифференцированием:
. Проверим этот результат дифференцированием:
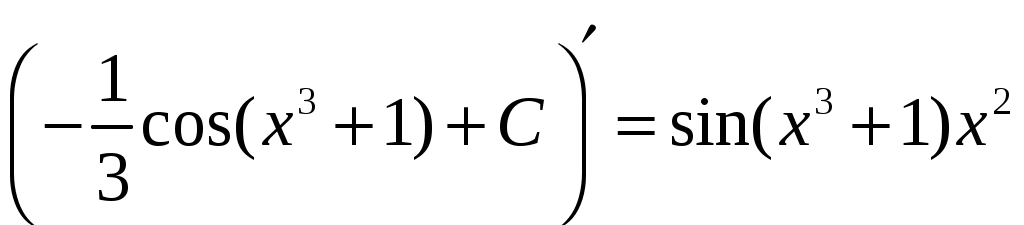 .
.
б) . Применим формулу интегрирования по частям
. Применим формулу интегрирования по частям 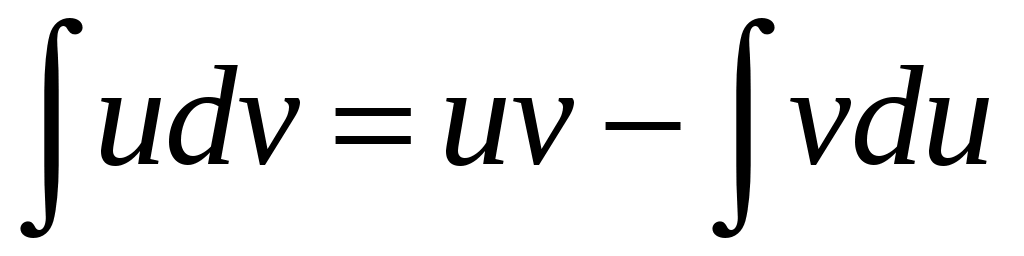 . Пусть
. Пусть 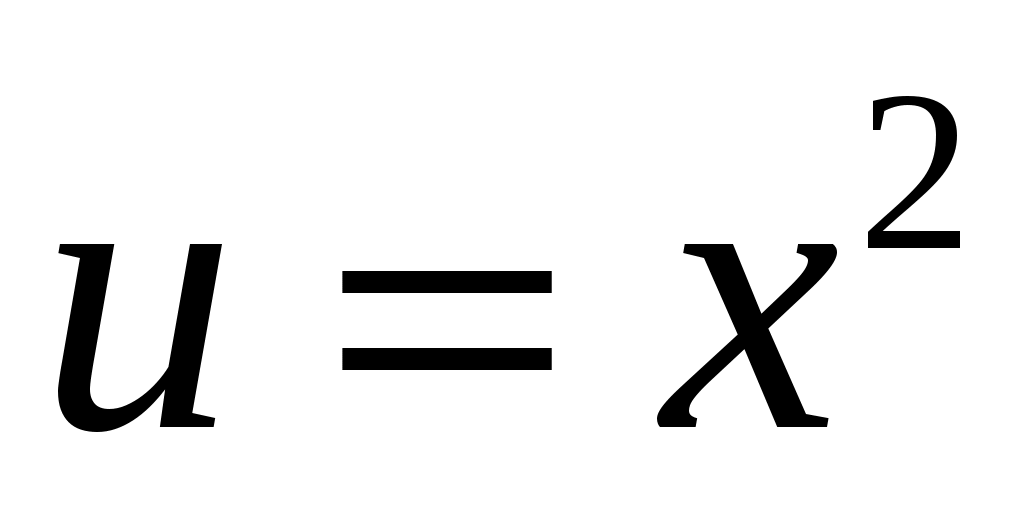 ,
, 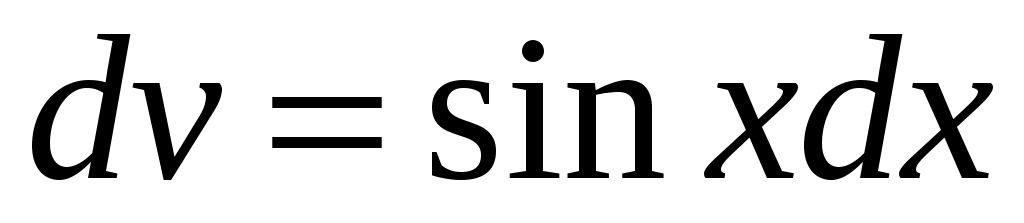 , тогда
, тогда 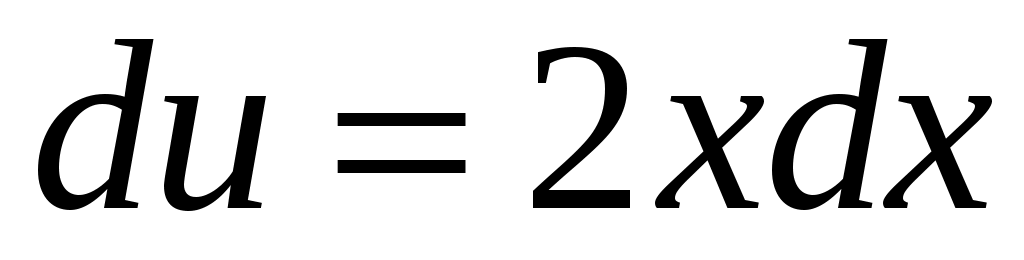 ,
, 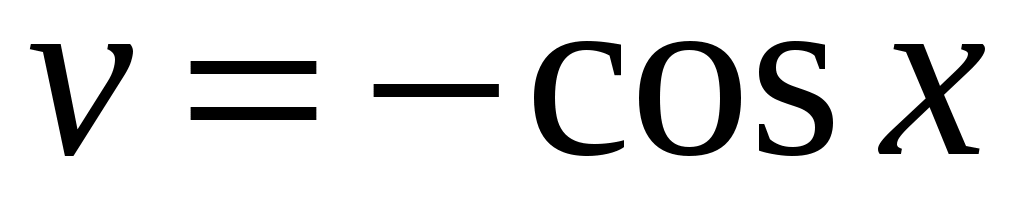 , и
, и 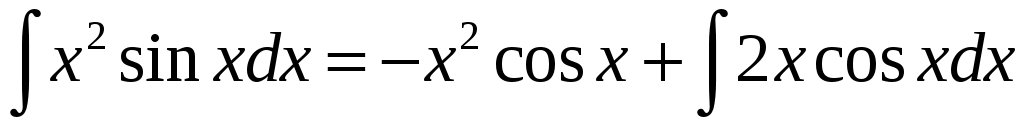 . К интегралу в правой части снова применяем формулу интегрирования по частям. Пусть
. К интегралу в правой части снова применяем формулу интегрирования по частям. Пусть 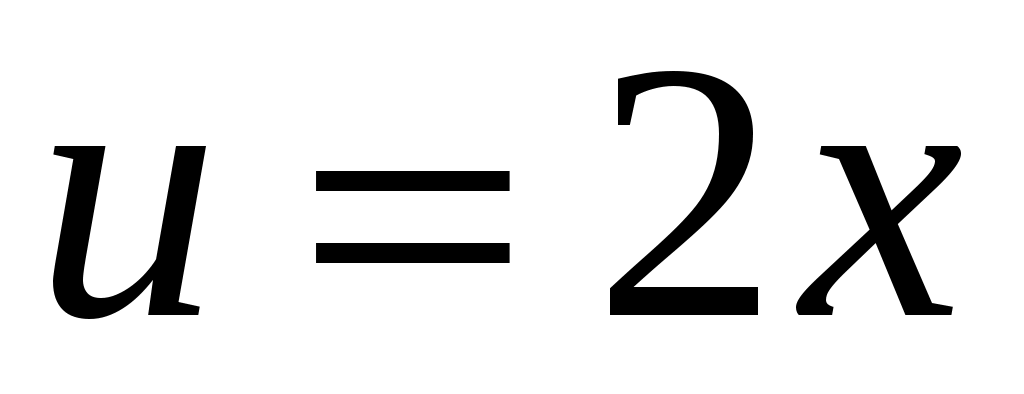
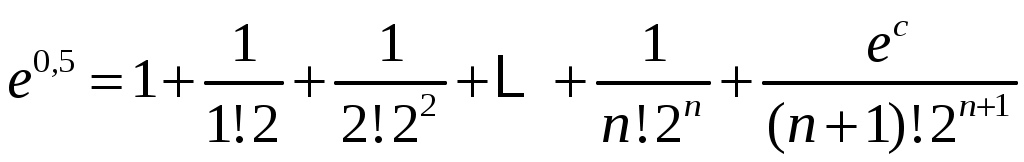 .
.Определим число n так, чтобы погрешность приближенного равенства
 . Так как
. Так как 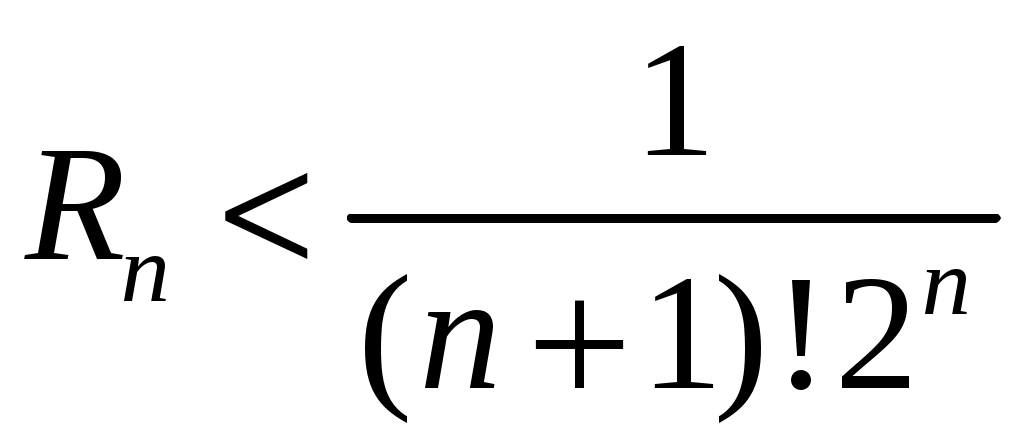 . Путем подбора найдём, при каком наименьшем n будет
. Путем подбора найдём, при каком наименьшем n будет Задание №9. Общая схема исследования функции и построения графика.
1. Найти область определения функции.
2. Определить тип функции (четность, нечетность).
3. Найти точки пересечения с осями координат и интервалы знакопостоянства функции.
4. Найти асимптоты графика функции:
а) вертикальные; б) невертикальные (наклонные).
5. Найти точки возможного экстремума и интервалы возрастания и убывания функции.
6. Найти точки перегиба и интервалы выпуклости, вогнутости функции.
7. Найти дополнительные точки.
8. Построить график функции, учитывая проведенные исследования.
Пример. Исследовать функцию
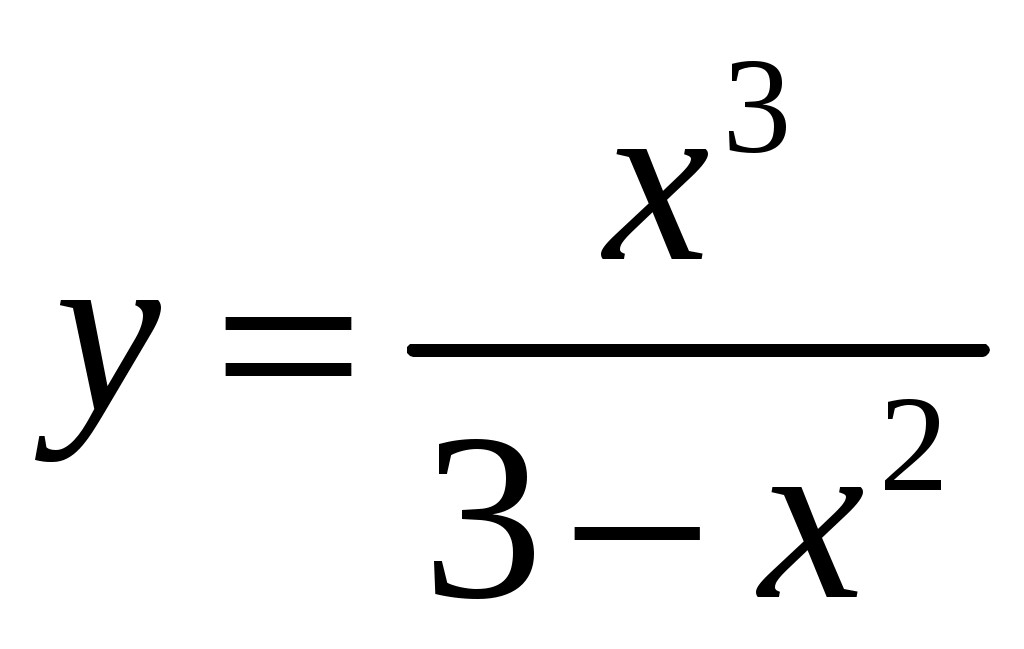 и построить ее график.
и построить ее график. Решение
1. Функция определена на
2. Так как
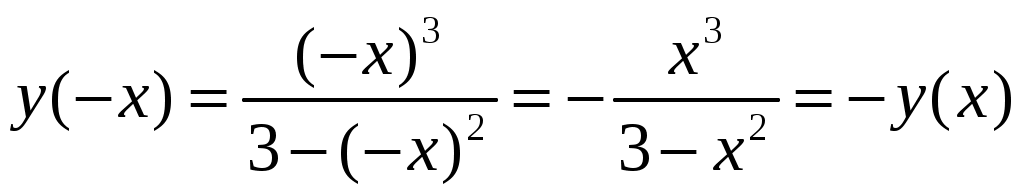 , то функция
, то функция нечетная.
3.
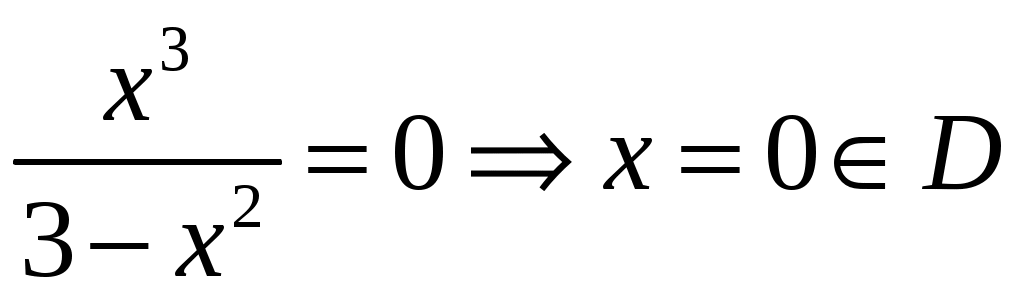 .
.| | | | 0 | | |
| знак | + | - | 0 | + | - |
| Расположение графика | Выше оси ОХ | Ниже оси ОХ | Пересекает ось ОХ | Выше оси ОХ | Ниже оси ОХ |
4. а) Вертикальные асимптоты:
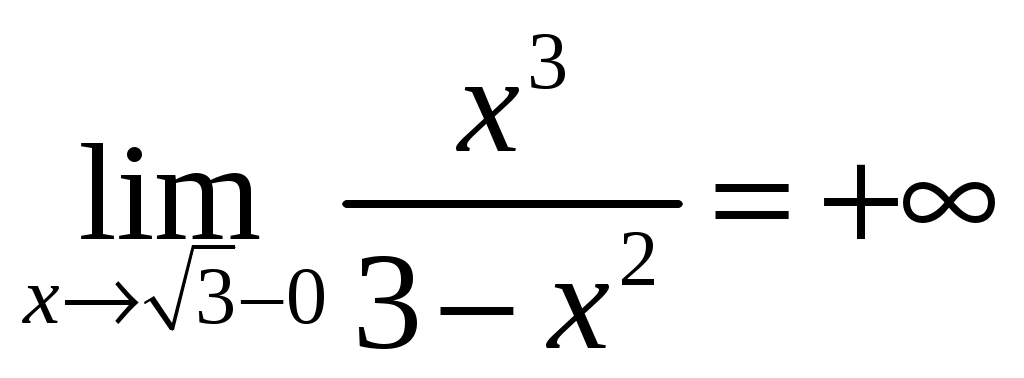 ;
; 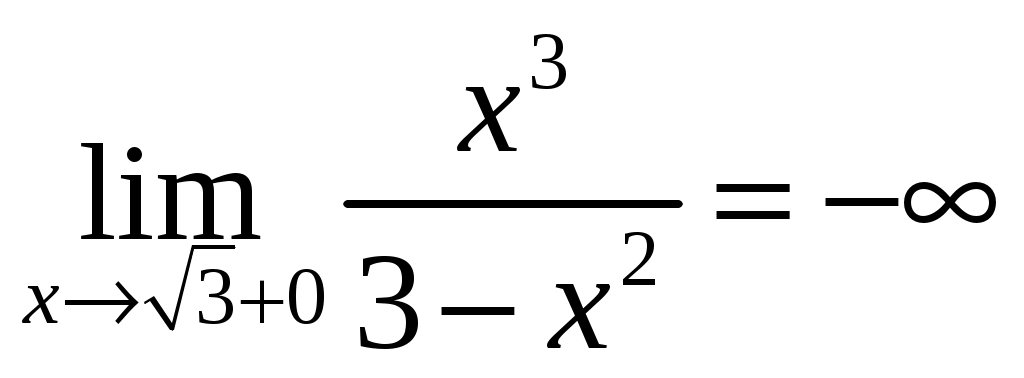 .
.Следовательно,
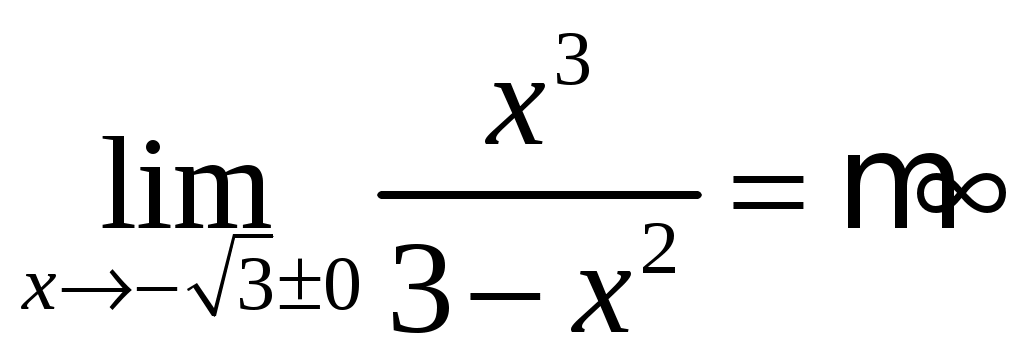 и
и б) Наклонные асимптоты
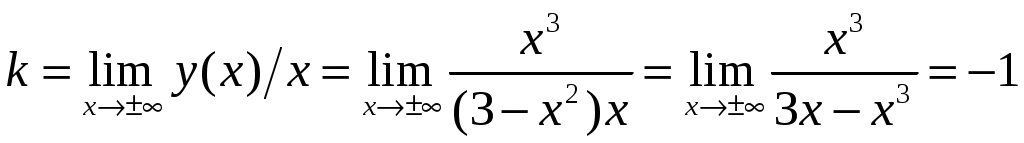 ;
; .
.Итак,
5.
 .
.Из уравнения
| X | | -3 | | | 0 | | | 3 | |
| | - | 0 | + | + | 0 | + | + | 0 | - |
| |   | 4,5 min | 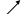 |  | Нет экст. |  |  | -4,5 max |  |
6.
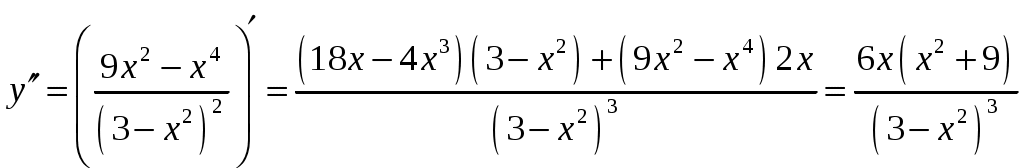 . Из уравнения
. Из уравнения 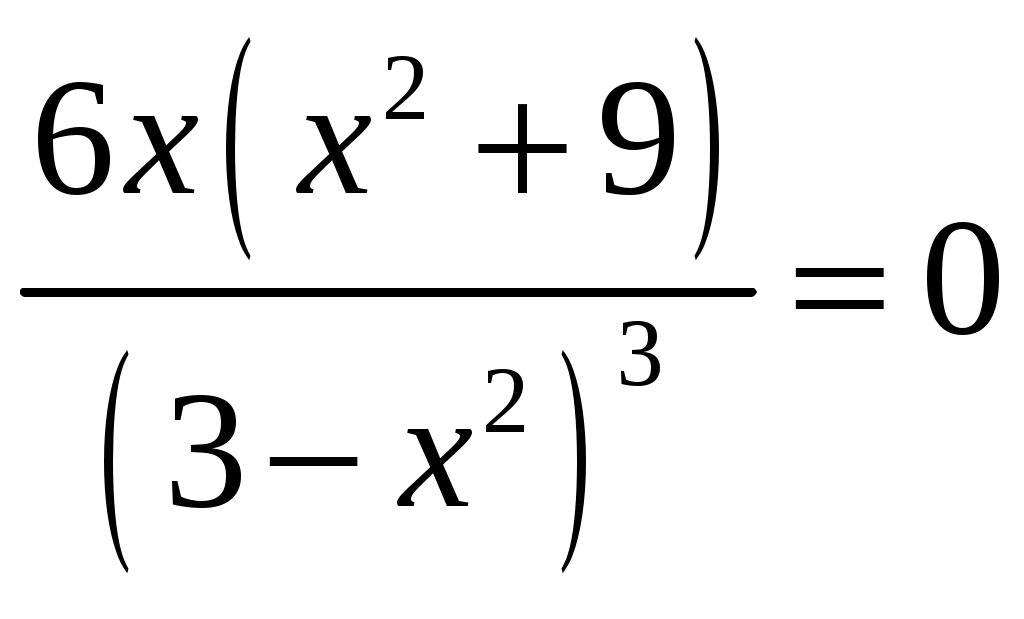 находим, что
находим, что | | | | 0 | | |
| Знак | + | - | 0 | + | - |
| Выпуклость | | | 0 | | |
7.Строим график функции.

3.2 Контрольная работа № 2. Семестр 2
Программой дисциплины «Математика» для студентов 1 курса во втором семестре предусмотрено выполнение контрольной работы № 2.
При выполнении контрольной работы № 2 необходимо изучить основные понятия и определения функции нескольких переменных. Научится вычислять частные производные. Научиться вычислять двойные интегралы через повторные. Изучить теорию числовых рядов. Необходимо знать основные признаки сходимости числовых рядов. Уметь вычислять радиус сходимости и, пользуясь им, интервал сходимости степенного ряда. Изучить теорию дифференциальных уравнений и научиться находить решения дифференциальных уравнений в простейших случаях. Изучить основные понятия теории вероятности: алгебру случайных событий, вероятность случайного события, условную вероятность случайного события, независимость двух случайных событий. Изучить основные понятия, связанные со случайными величинами. Уметь вычислять по известному закону распределения математическое ожидание и дисперсию.
Ниже приведены примеры выполнения заданий.
Задание № 1. Найти неопределенные интегралы, правильность результаты проверить дифференцированием.
Пример. Найти неопределенные интегралы.
а)
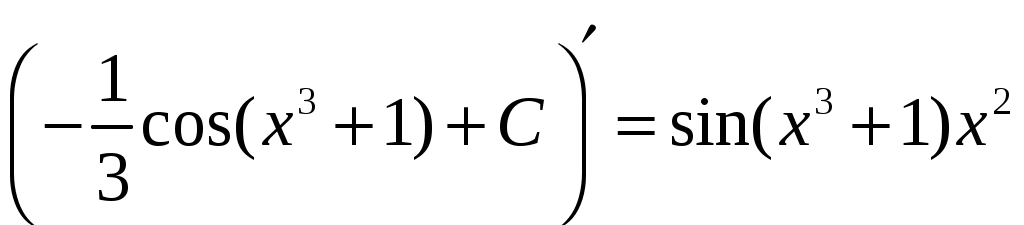 .
.б)