Файл: Методические указания по изучению дисциплины и выполнению контрольных работ для студентов заочной формы обучения направлений.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 127
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Тогда имеем 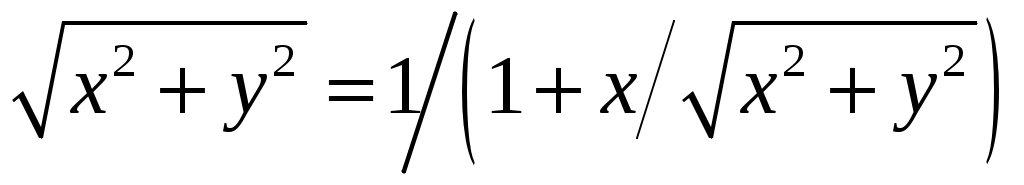 . Отсюда
. Отсюда 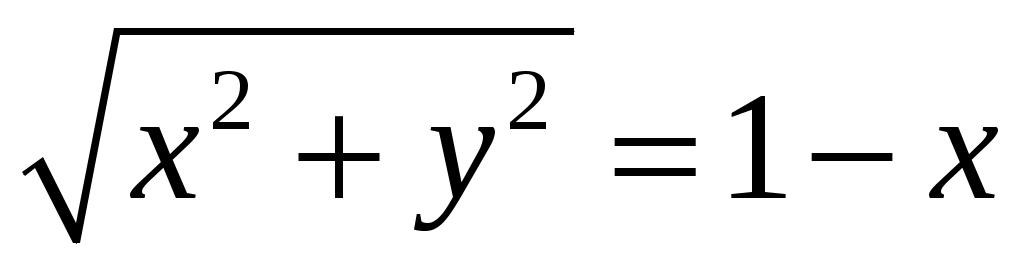 или , после возведения в квадрат и приведения подобных, получим каноническое уравнение параболы
или , после возведения в квадрат и приведения подобных, получим каноническое уравнение параболы 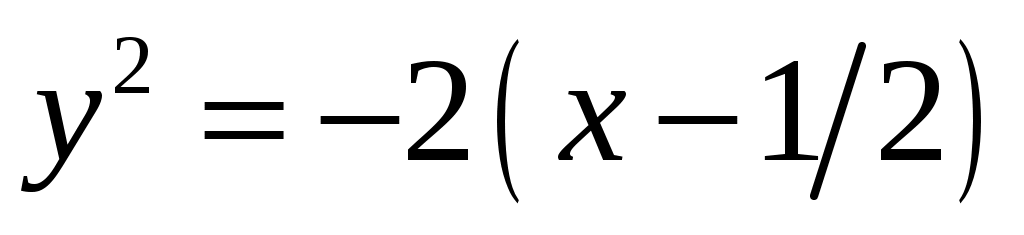 с вершиной в точке
с вершиной в точке 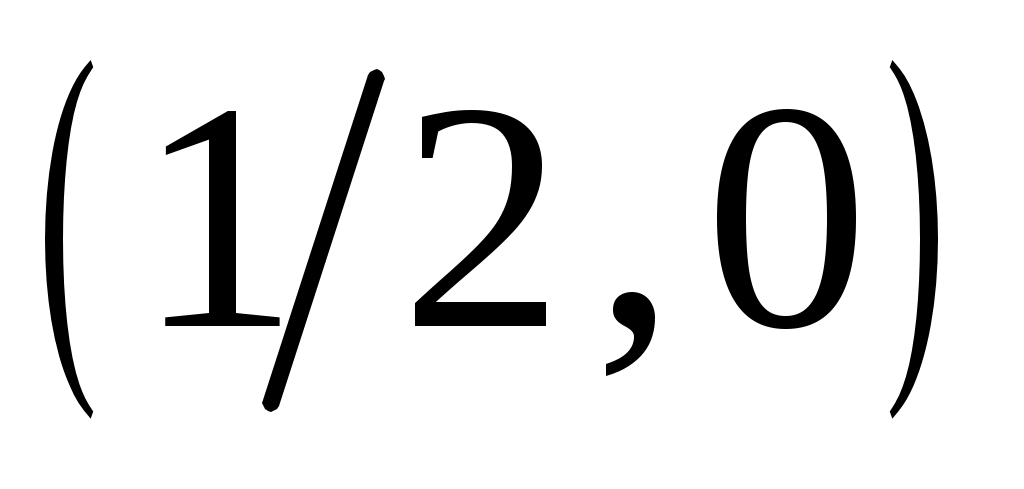 .
.
Задание №4. Найти решение системы с помощью правила Крамера для систем трех алгебраических уравнений с тремя неизвестными
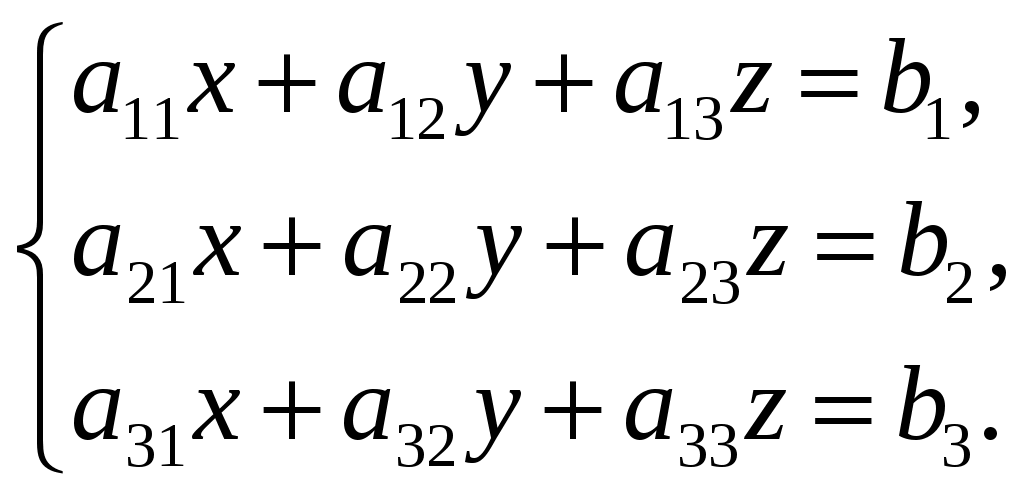
правило Крамера имеет вид: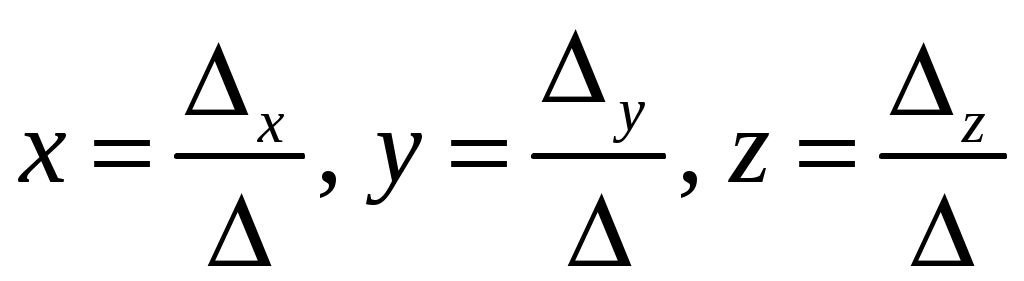 при условии
при условии 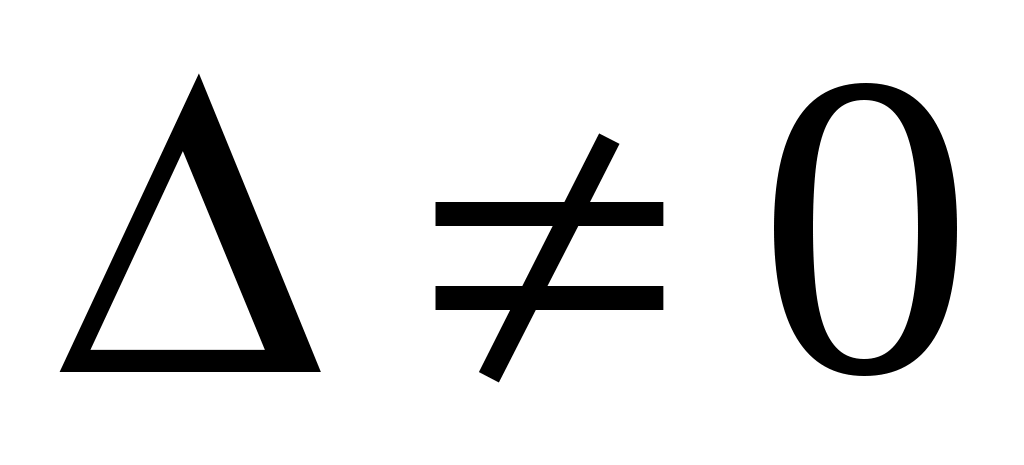 , где
, где
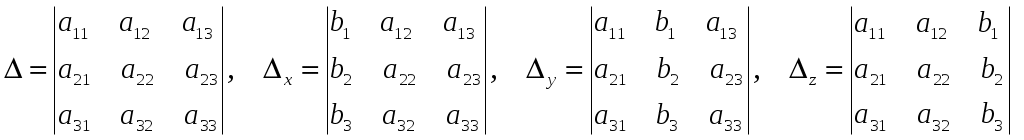 .
.
Определитель третьего порядка, обозначаемый символом
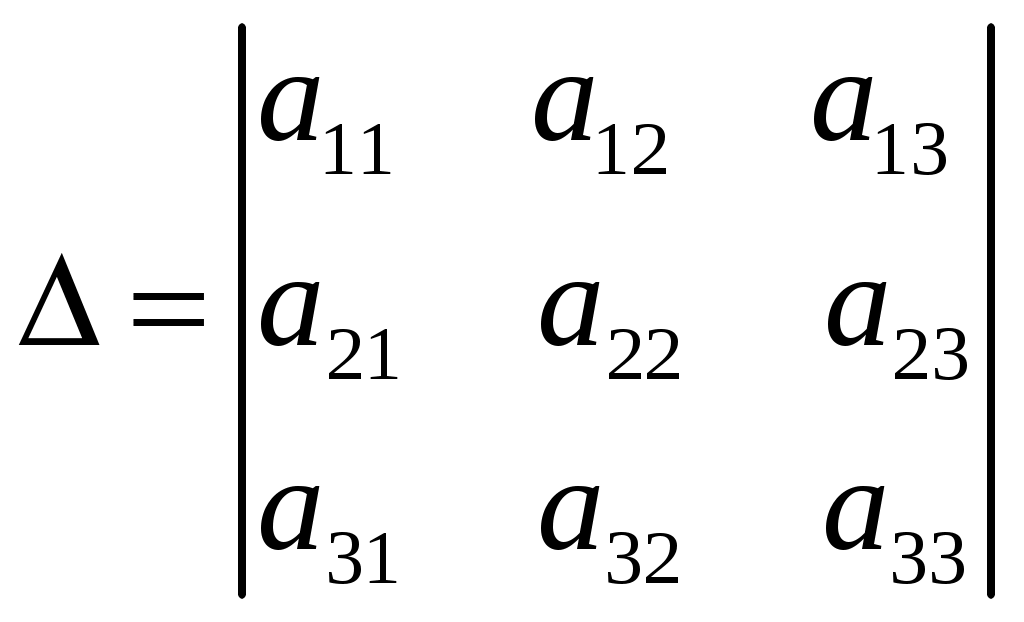 ,
,
вычисляется по правилу треугольника или Сариуса:
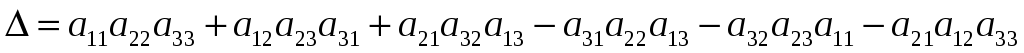 .
.
Например
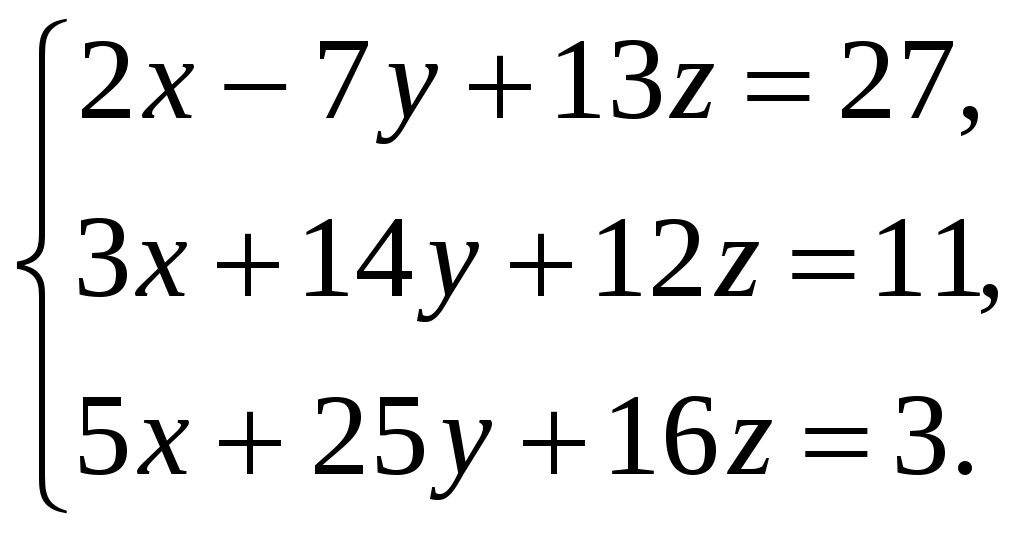
Решение.
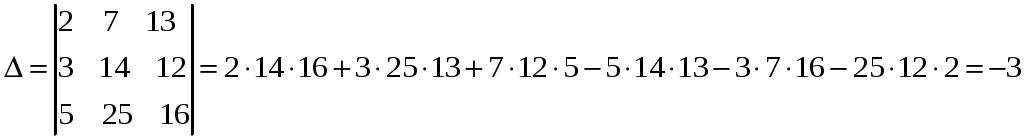
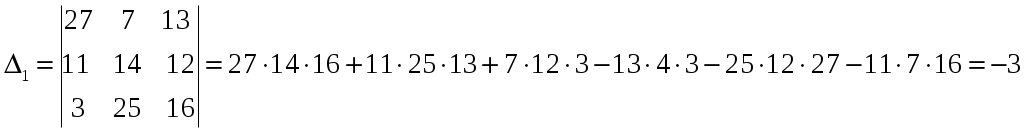
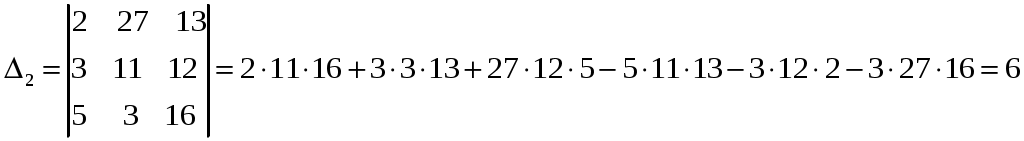
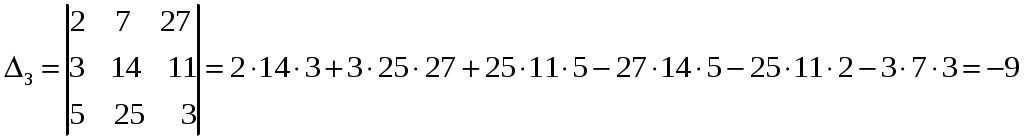
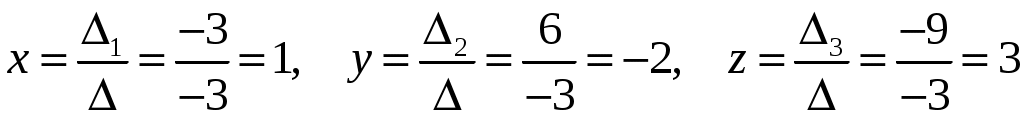 .
.
Ответ: (1, -2, 3).
Применение метода Гаусса приведено в примере к заданиям 1-10.
Задание № 5. Вычислить пределы функций, не пользуясь правилом Лопиталя.
При вычислении предела дробно-рациональной функции при получаем неопределенность типа
получаем неопределенность типа 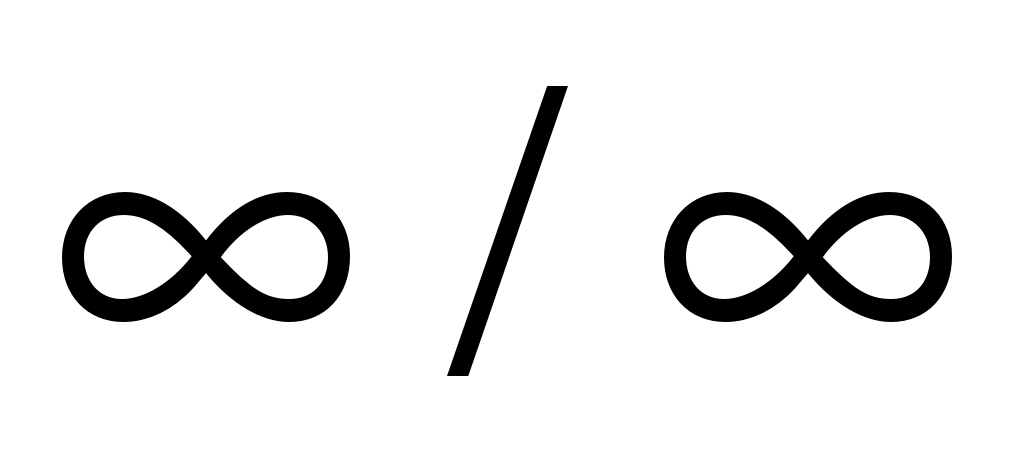 , для раскрытия которой нужно числитель и знаменатель дроби разделить на наивысшую степень х.
, для раскрытия которой нужно числитель и знаменатель дроби разделить на наивысшую степень х.
Пример 1.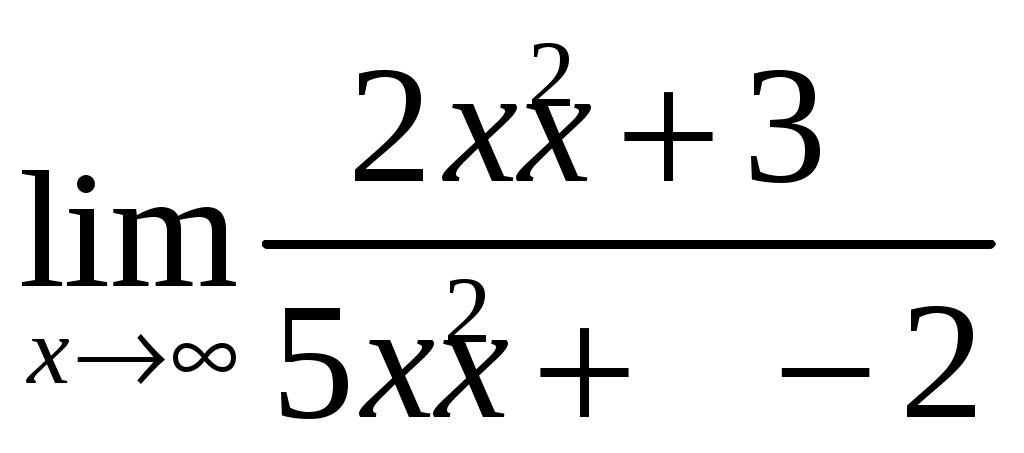 .
.
Решение. Разделим числитель и знаменатель на степень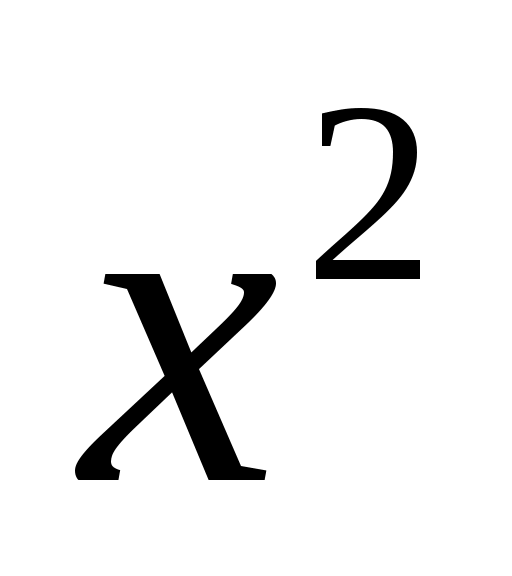 :
:
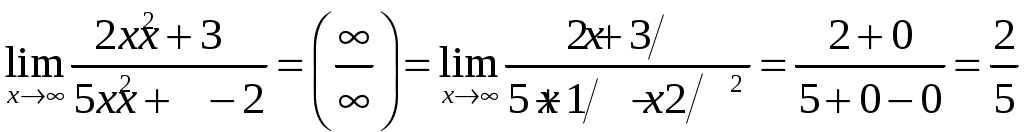 .
.
В том случае, когда при вычислении предела дробно-рациональной функции при числитель и знаменатель имеют неопределенность
числитель и знаменатель имеют неопределенность 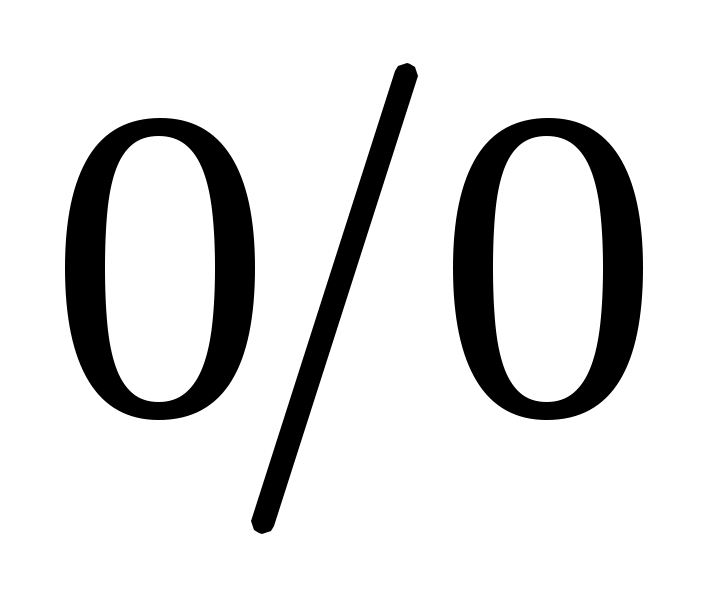 , надо разделить их на
, надо разделить их на 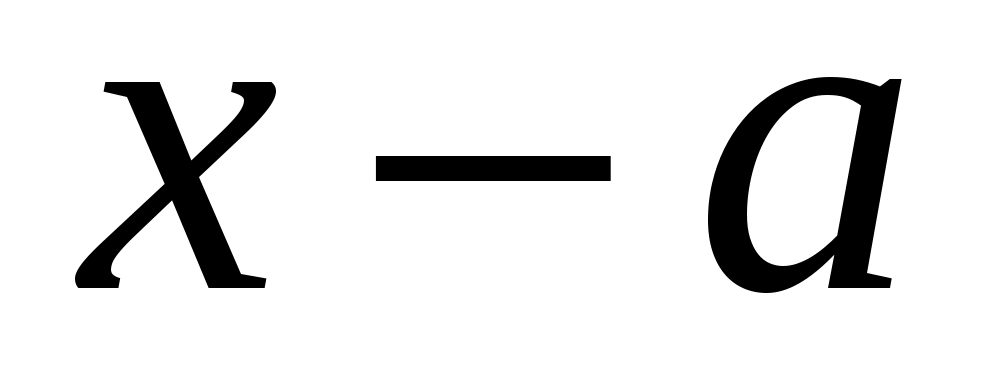 и перейти к пределу. Если после деления окажется, что при
и перейти к пределу. Если после деления окажется, что при  числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на
числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на 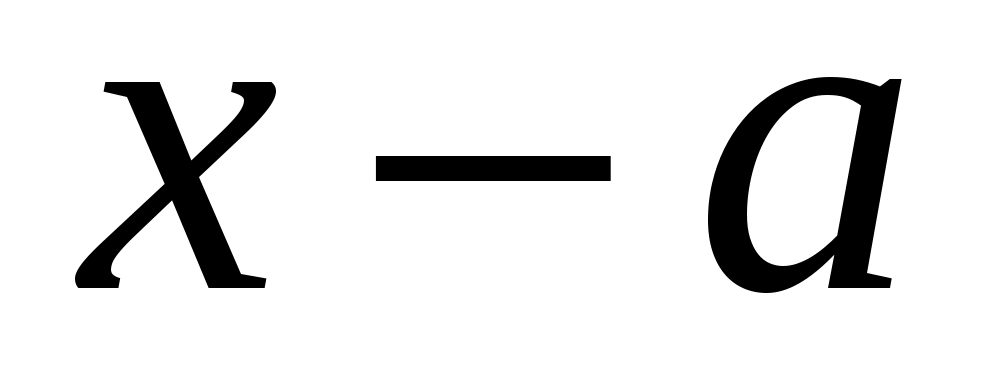 .
.
Пример 2.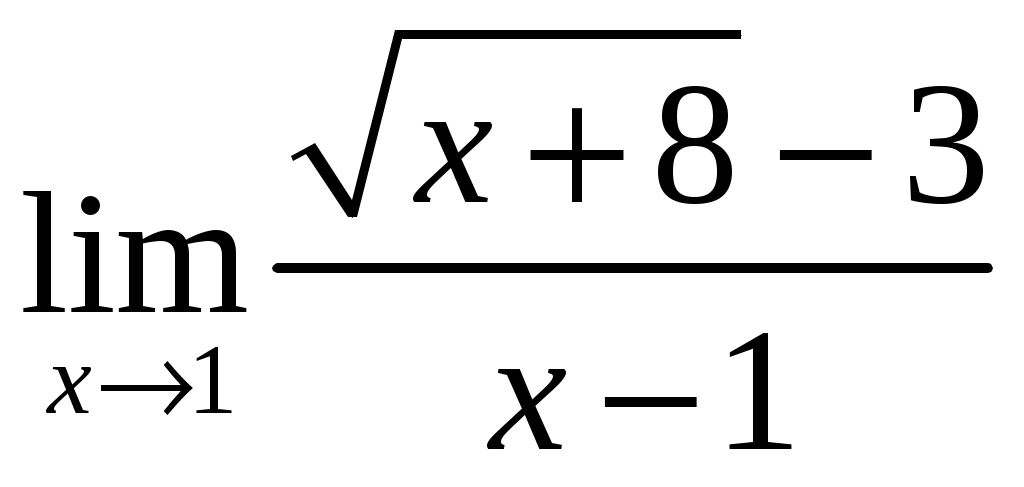 .
.
Решение. Здесь мы имеем неопределенность вида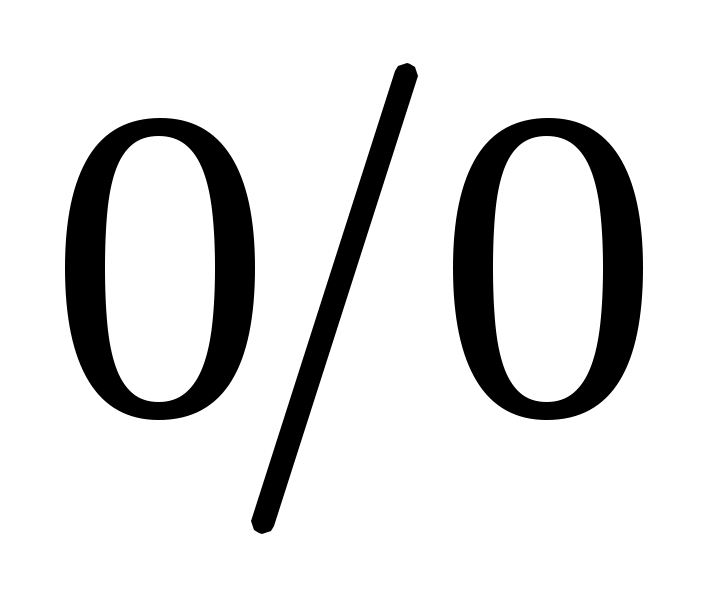 . До множим числитель и знаменатель дроби на выражение, сопряженное числителю (избавимся от иррациональности в числителе):
. До множим числитель и знаменатель дроби на выражение, сопряженное числителю (избавимся от иррациональности в числителе):
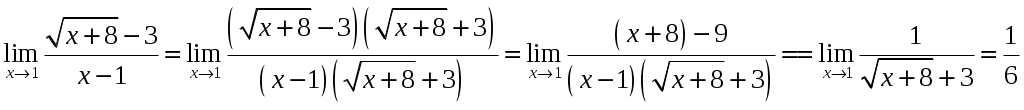 .
.
При вычислении пределов тригонометрических функций часто используется первый замечательный предел и его следствия:
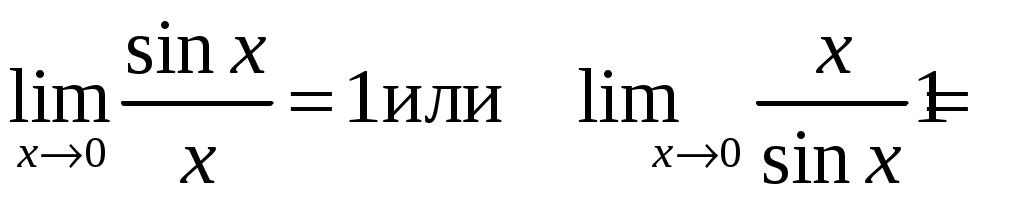 ;
; 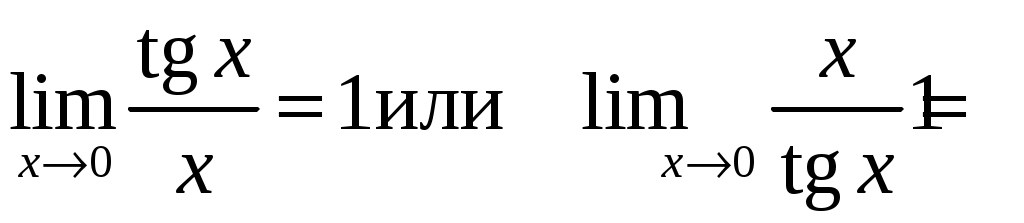 .
.
Пример 3.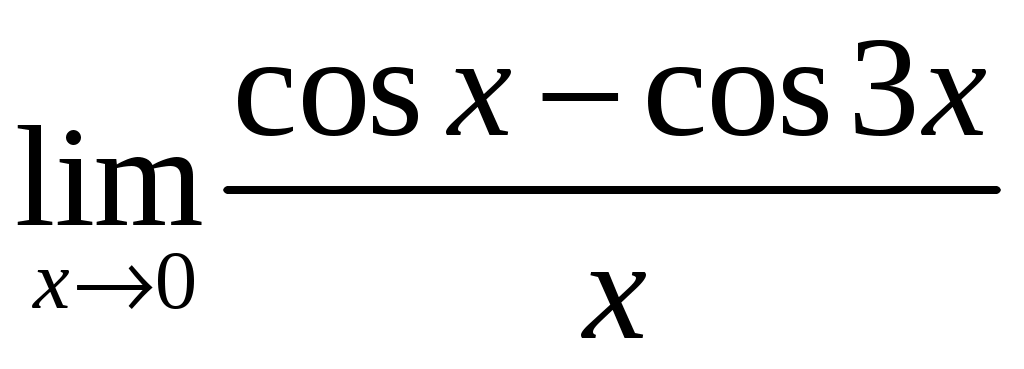 .
.
Решение. Преобразовав разность косинусов в произведение, получим
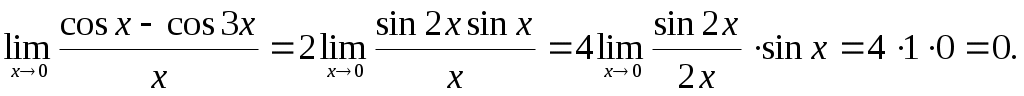
Если в пределе получаем неопределенность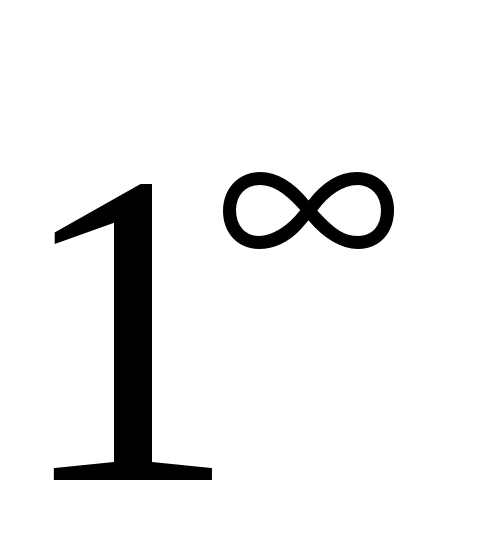 , то используем
, то используем
второй замечательный предел.
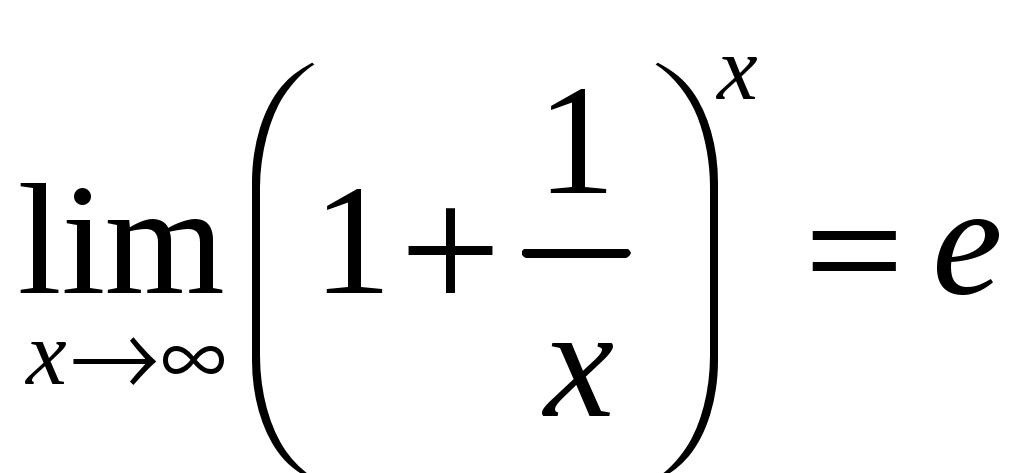 или
или 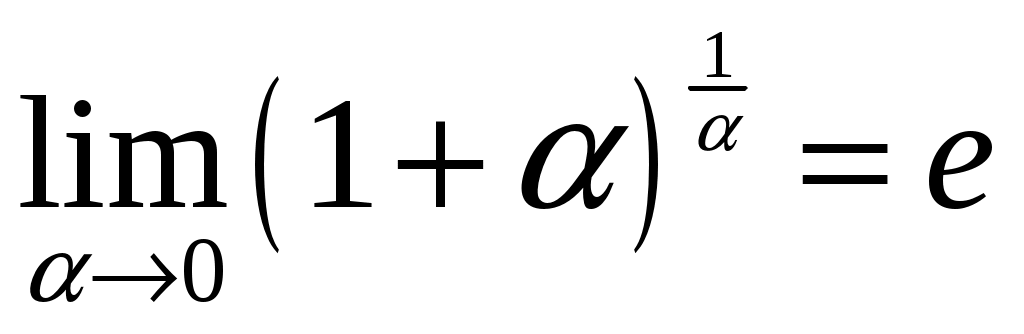 (2)
(2)
Пример 4.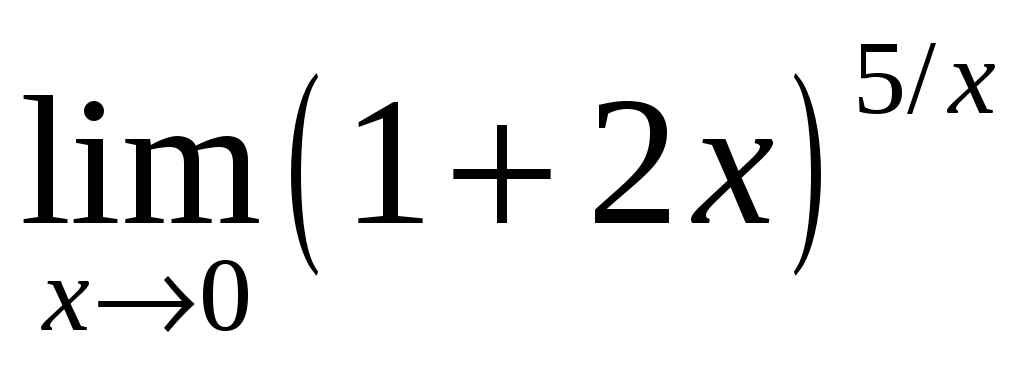 .
.
Решение. Выполнив преобразования и применив второй замечательный предел, найдём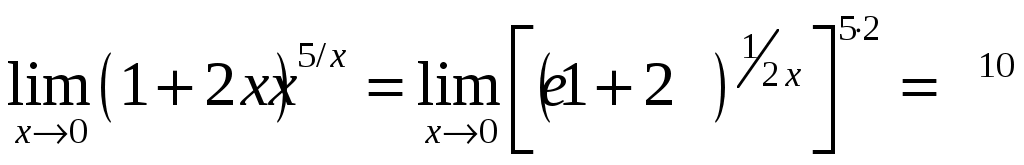 .
.
Пример 5.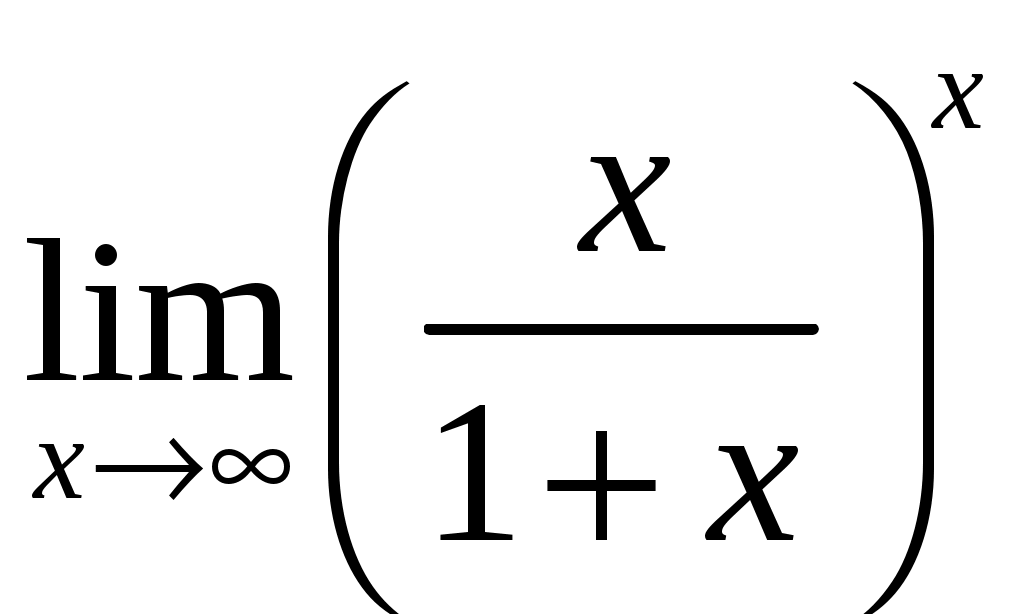 .
.
Решение. Выполнив преобразования и применив формулу (2), найдём
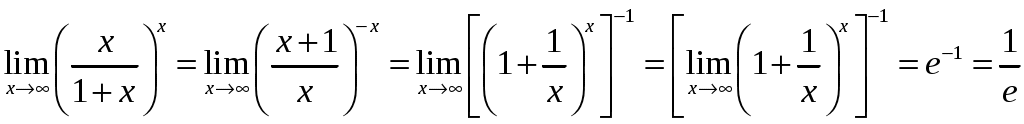 .
.
Задание №6. Задана функция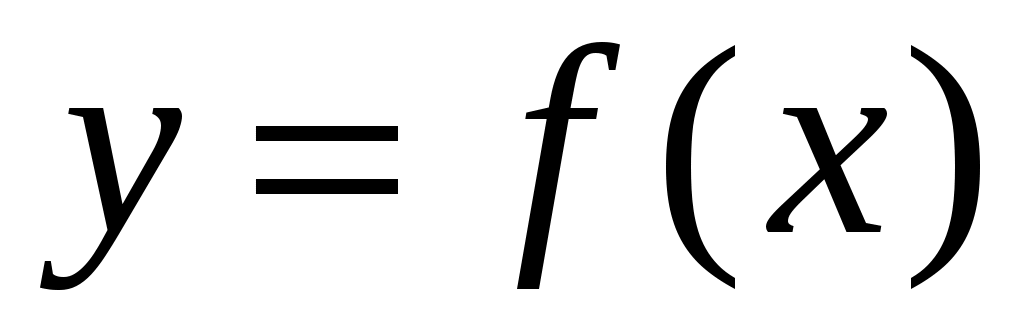 . Найти точки разрыва и определить их тип. Сделать схематический чертеж.
. Найти точки разрыва и определить их тип. Сделать схематический чертеж.
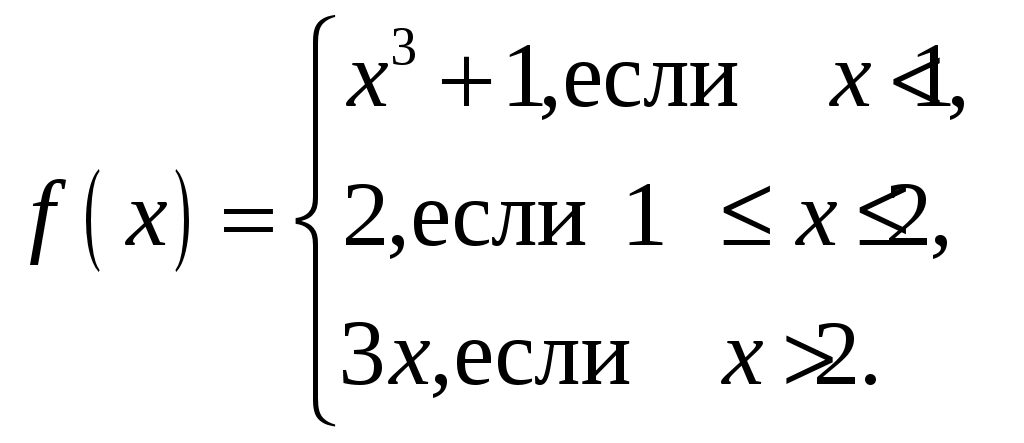
Решение. Функции
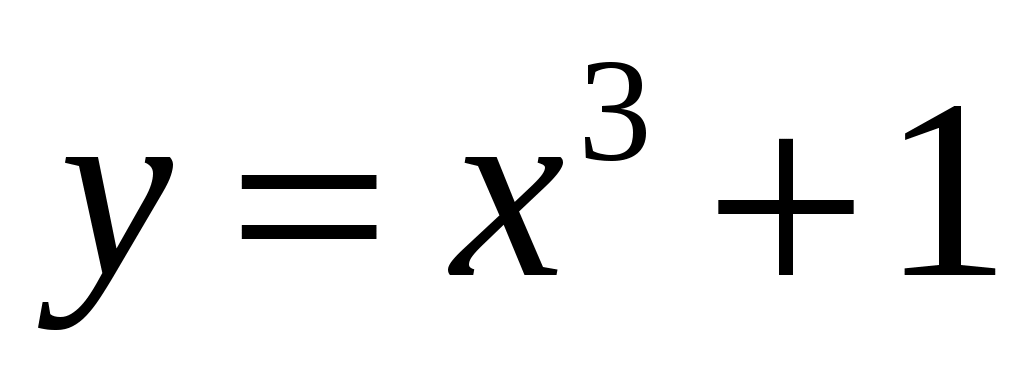 ,
, 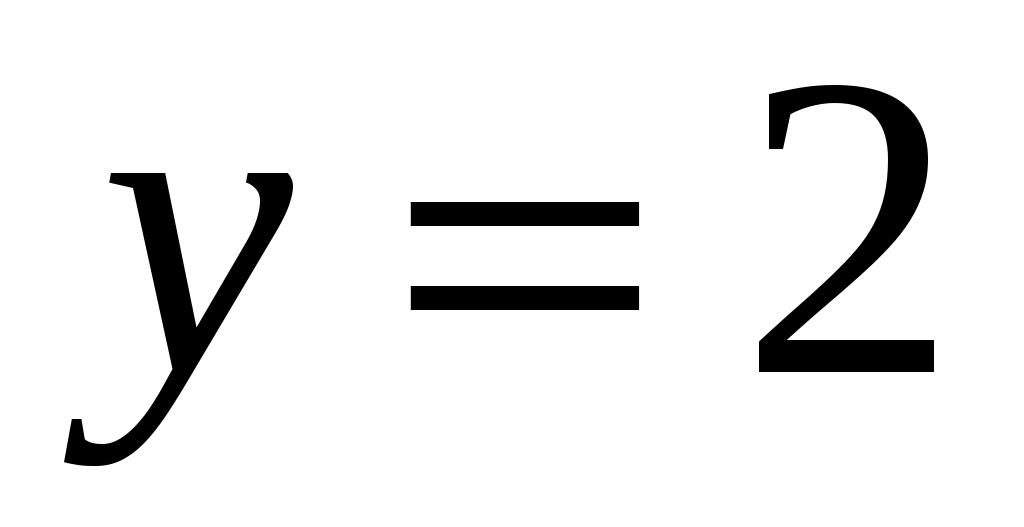 , и
, и 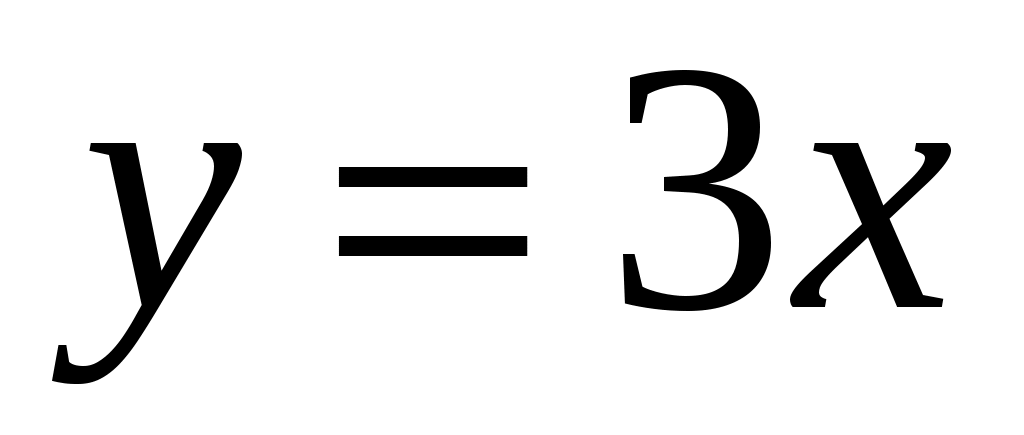 непрерывны на всей числовой прямой, поэтому данная функция может иметь разрывы только в точках, где меняется ее аналитическое выражение, т.е. в точках
непрерывны на всей числовой прямой, поэтому данная функция может иметь разрывы только в точках, где меняется ее аналитическое выражение, т.е. в точках 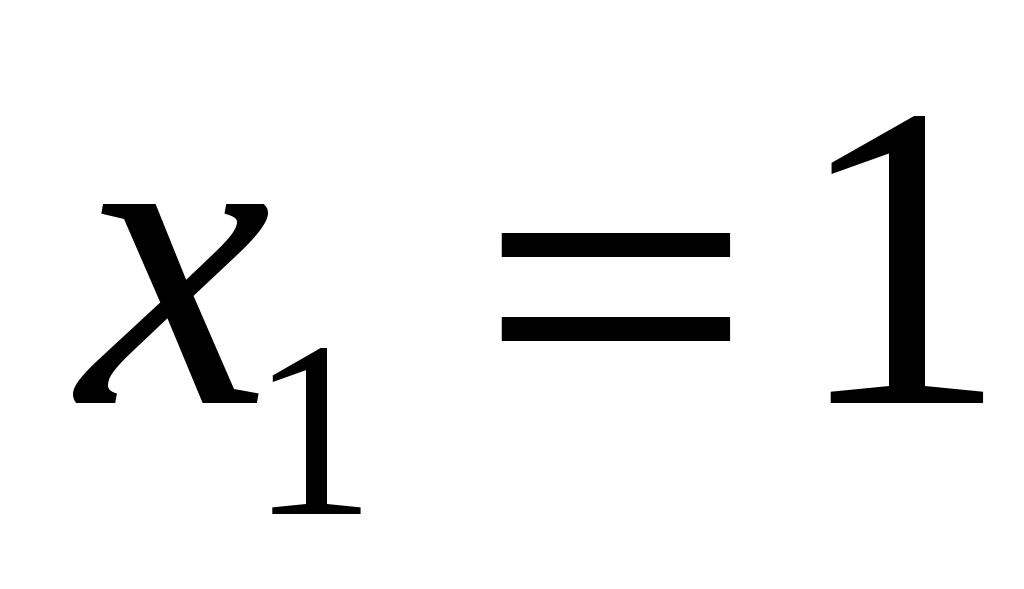 и
и 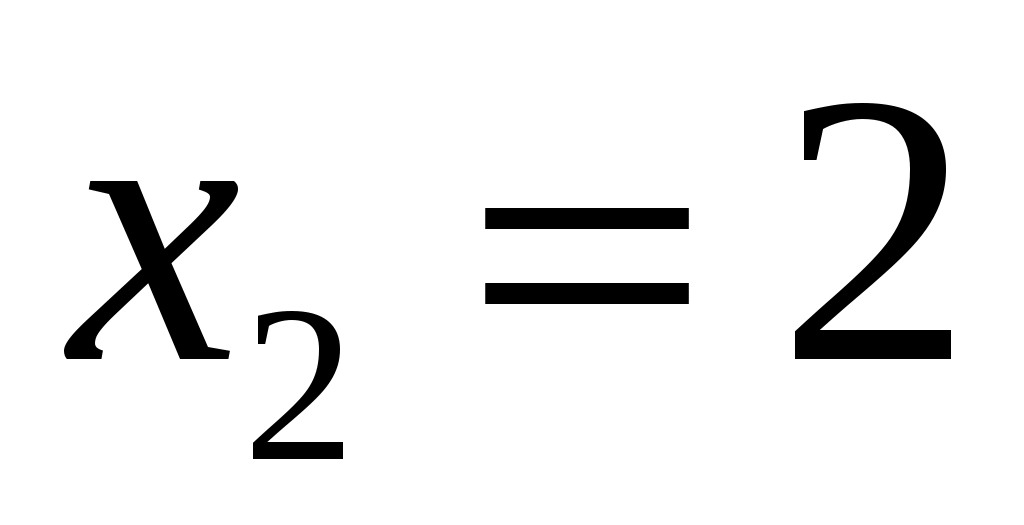 . Исследуем функцию на непрерывность в этих точках, для чего найдем соответствующие односторонние пределы и значения функции.
. Исследуем функцию на непрерывность в этих точках, для чего найдем соответствующие односторонние пределы и значения функции.
В точке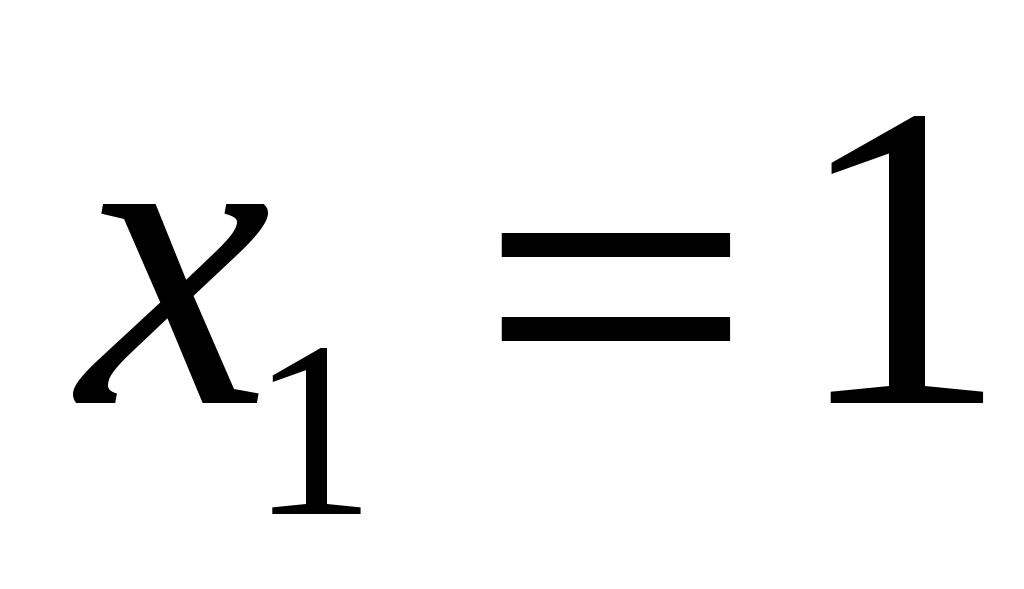 :
: 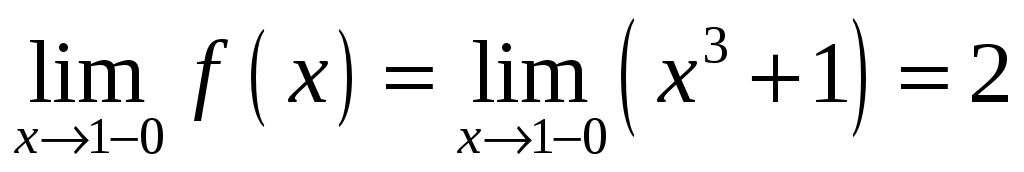 ,
, 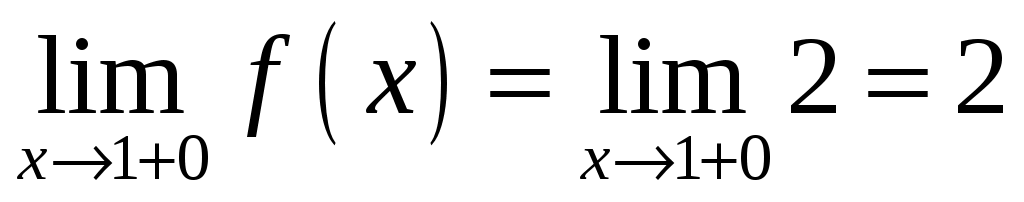 ,
, 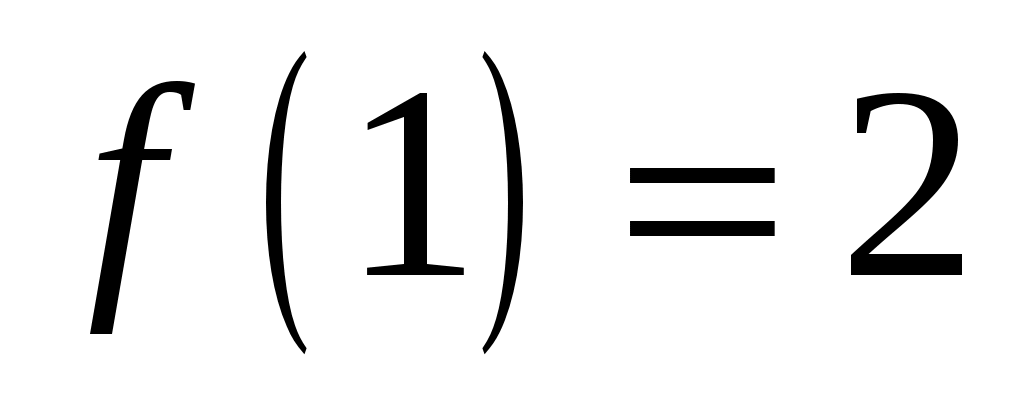 .
.
Таким образом,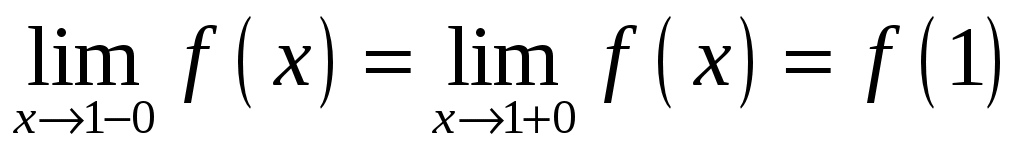 . Значить, функция непрерывна в точке
. Значить, функция непрерывна в точке 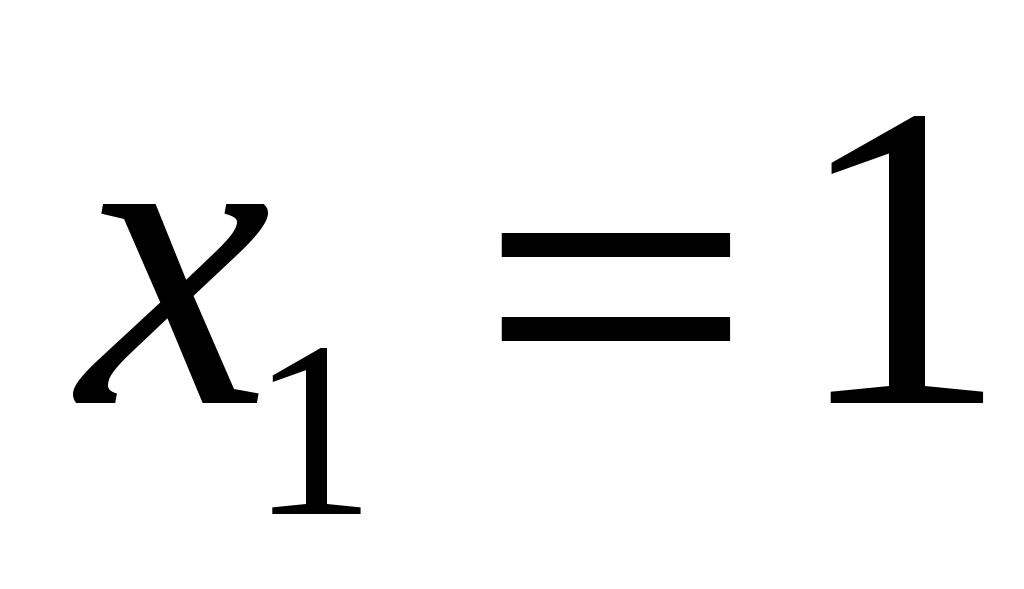
.
В точке :
: 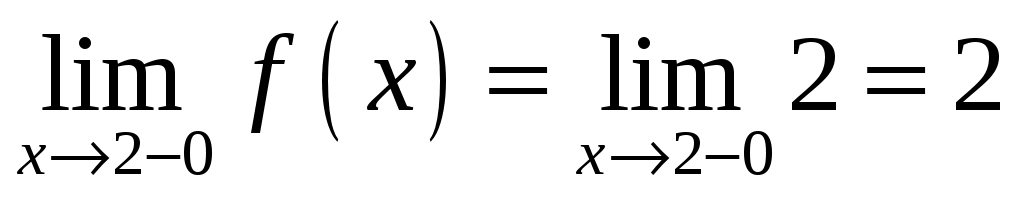 ,
, 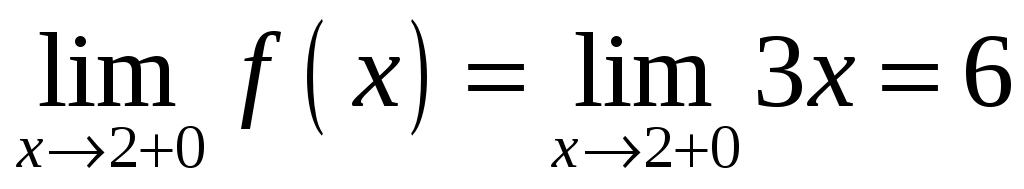 ,
, 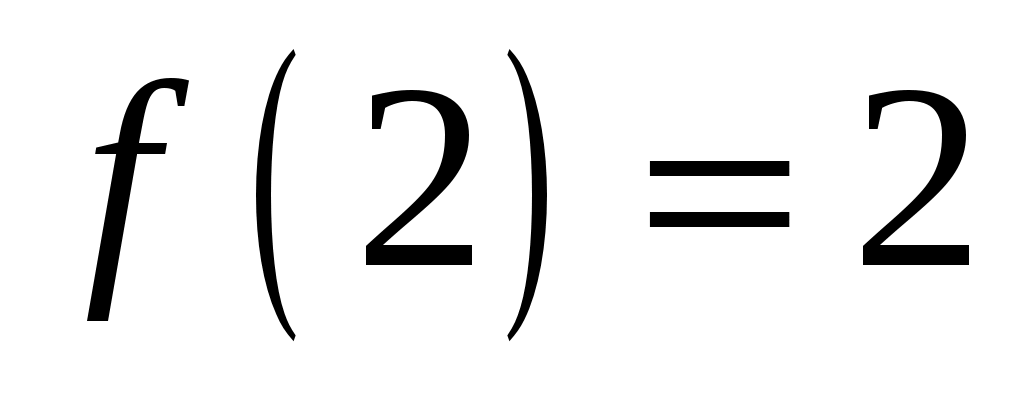 .
.
Таким образом,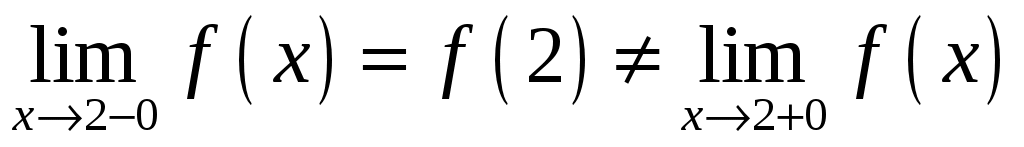 , т.е. функция имеет разрыв Ι рода и непрерывна слева. Скачок функции
, т.е. функция имеет разрыв Ι рода и непрерывна слева. Скачок функции 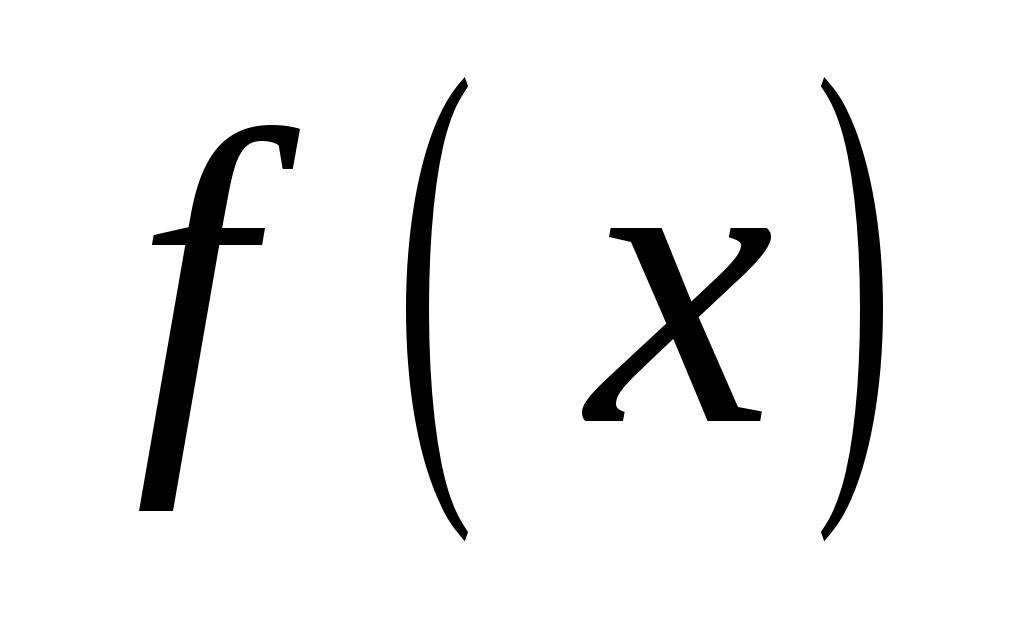 в точке
в точке  равен ∆
равен ∆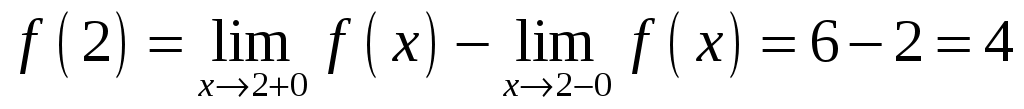 . График функции изображен на рисунке
. График функции изображен на рисунке
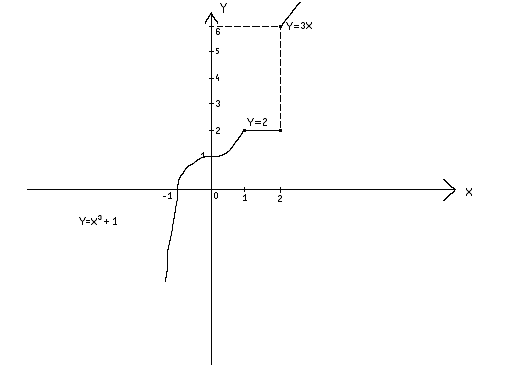
При выполнении следующего задания необходимо знать правила вычисления производной (производная суммы, произведения и частного дух функций), а также изучить таблицу производных.
Задание №7. Найти производные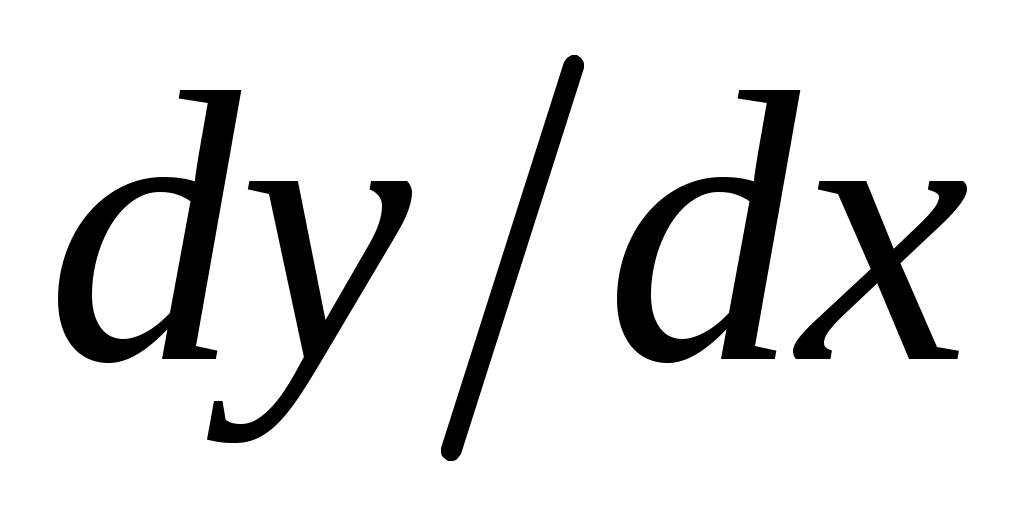 данных функций.
данных функций.
а)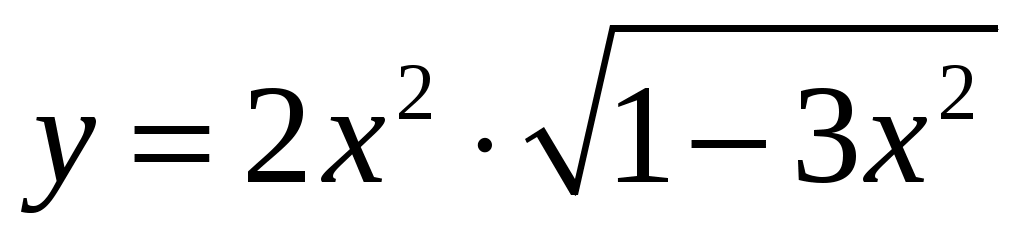 .
.
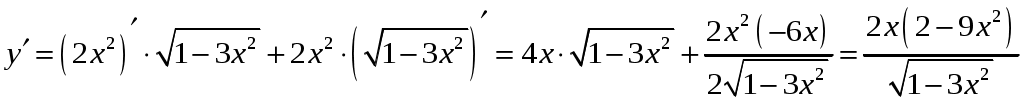 .
.
б)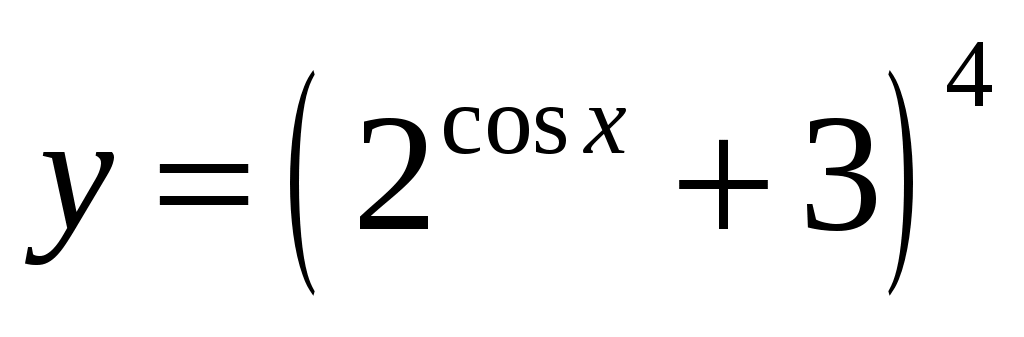 .
. 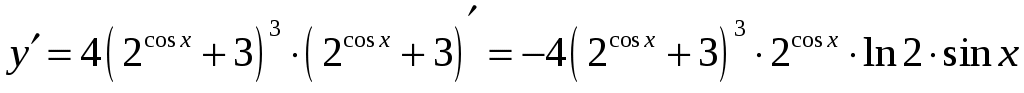 .
.
в)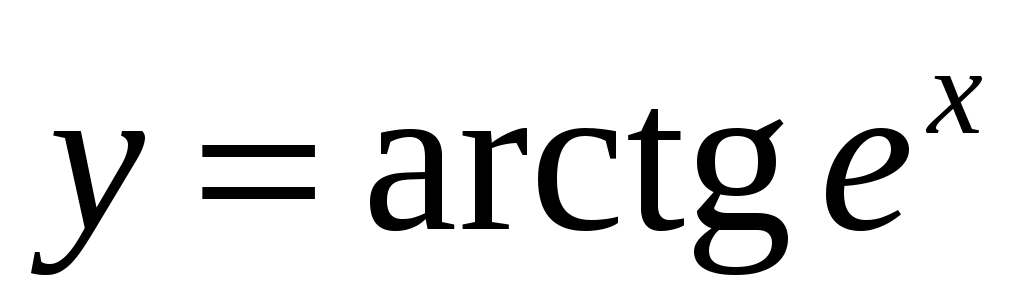 .
.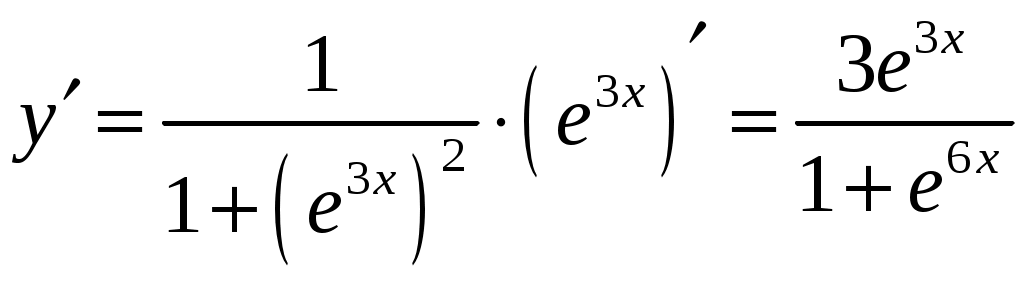 .
.
г)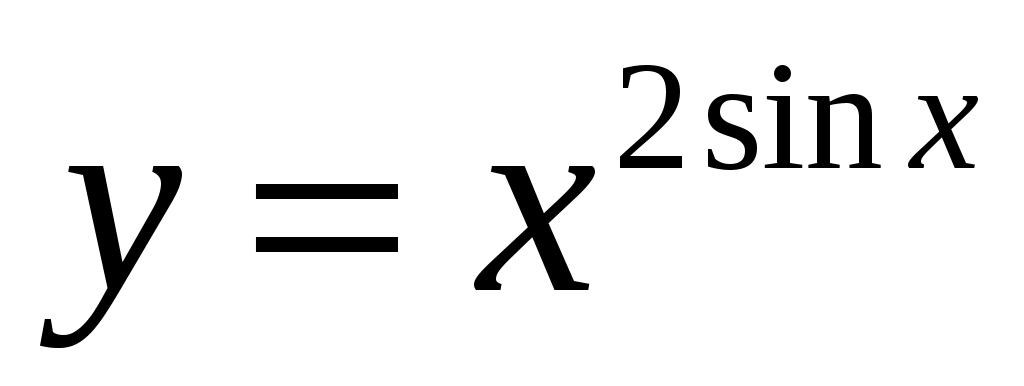 .
.
Прологарифмируем обе части равенства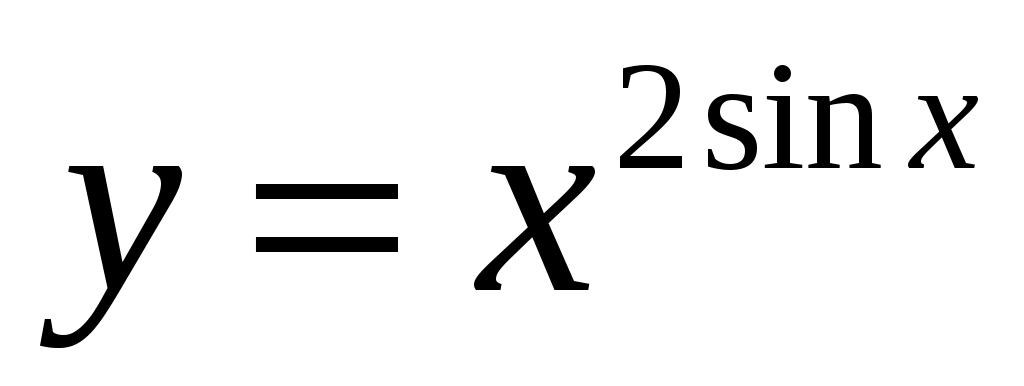 . Тогда
. Тогда 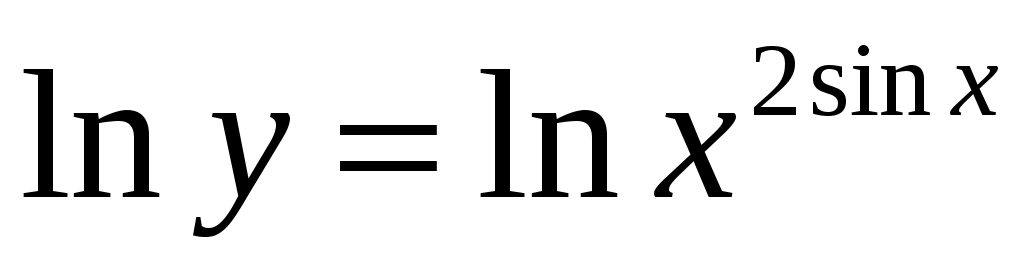 , т.е.
, т.е. 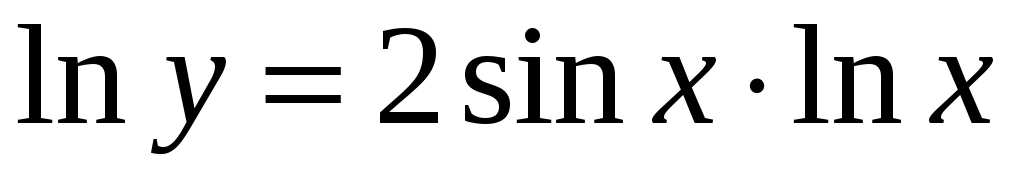 . Теперь продифференцируем последнее равенство
. Теперь продифференцируем последнее равенство 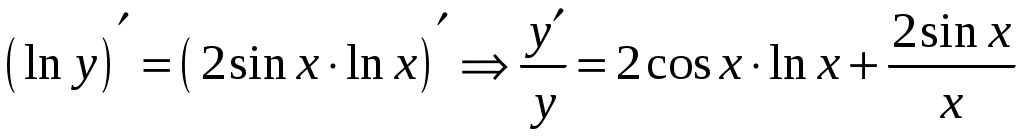 Откуда получаем
Откуда получаем 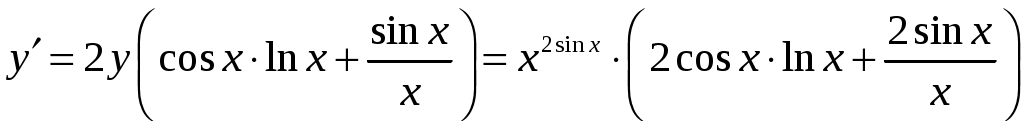 .
.
д)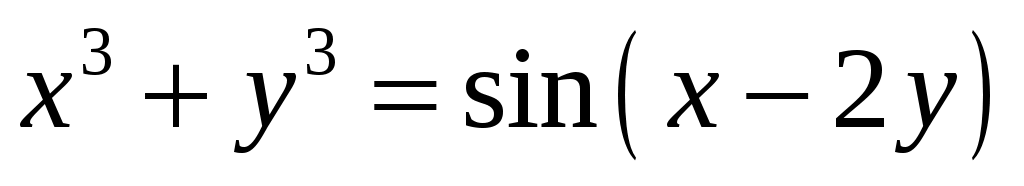 .
.
Продифференцируем обе части уравнения по x, учитывая, что y есть функция от x. Тогда получим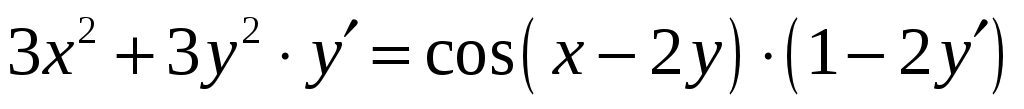 . Отсюда -
. Отсюда - 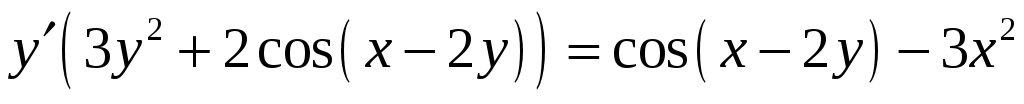 т.е.
т.е. 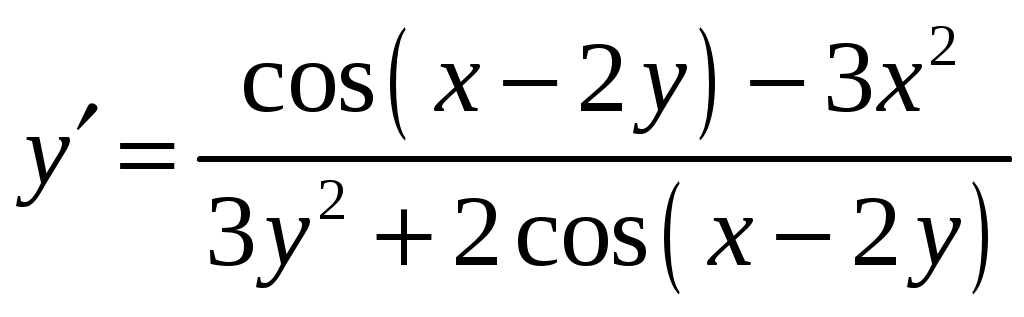 .
.
Задание №8. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции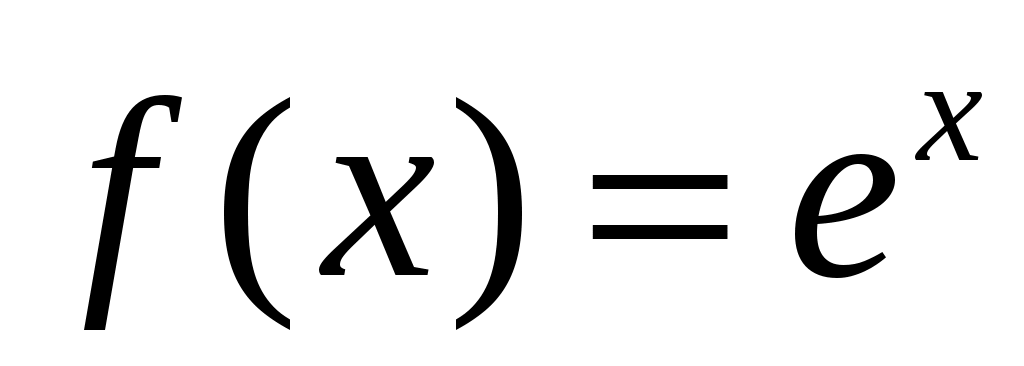 , вычислить значение
, вычислить значение 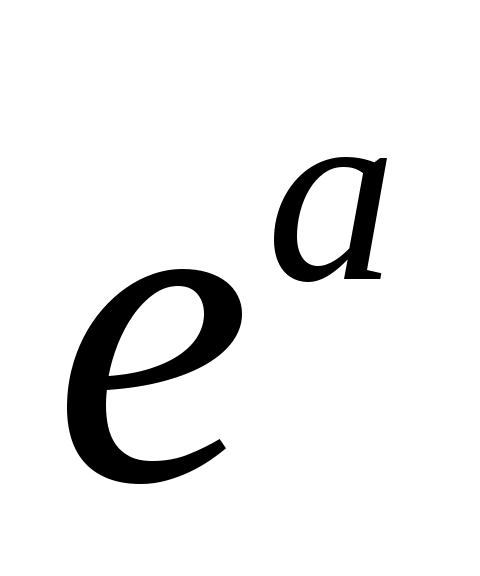 с точностью до 0,0001. a=0,5.
с точностью до 0,0001. a=0,5.
Решение. Разложим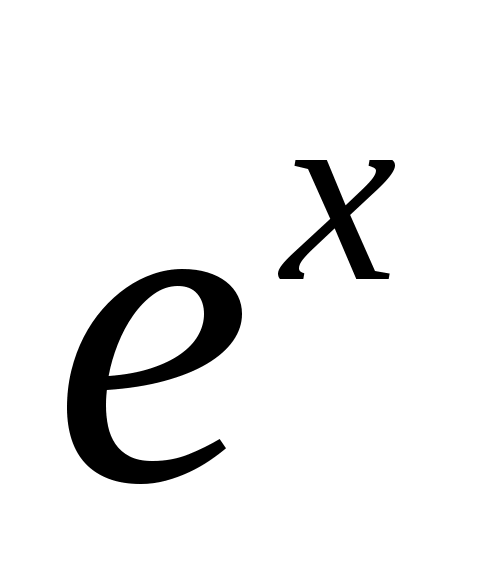 по формуле Тейлора n-го порядка
по формуле Тейлора n-го порядка
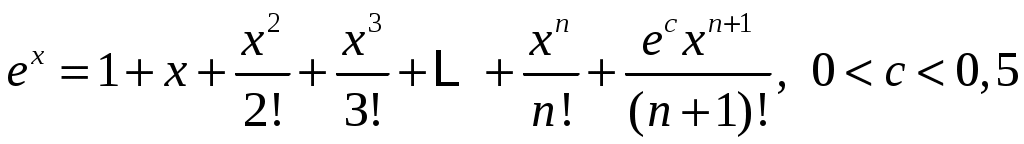 .
.
Положив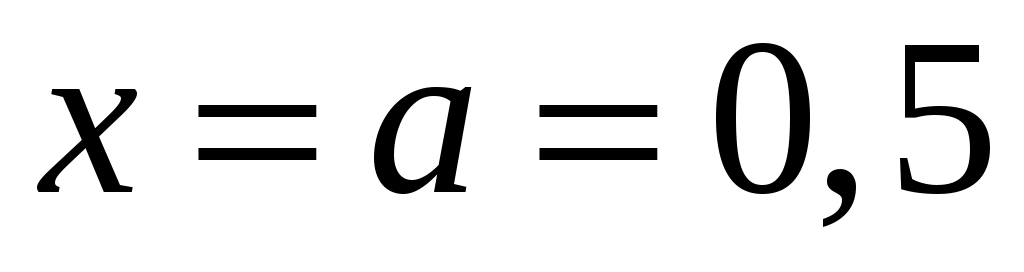
Задание №4. Найти решение системы с помощью правила Крамера для систем трех алгебраических уравнений с тремя неизвестными
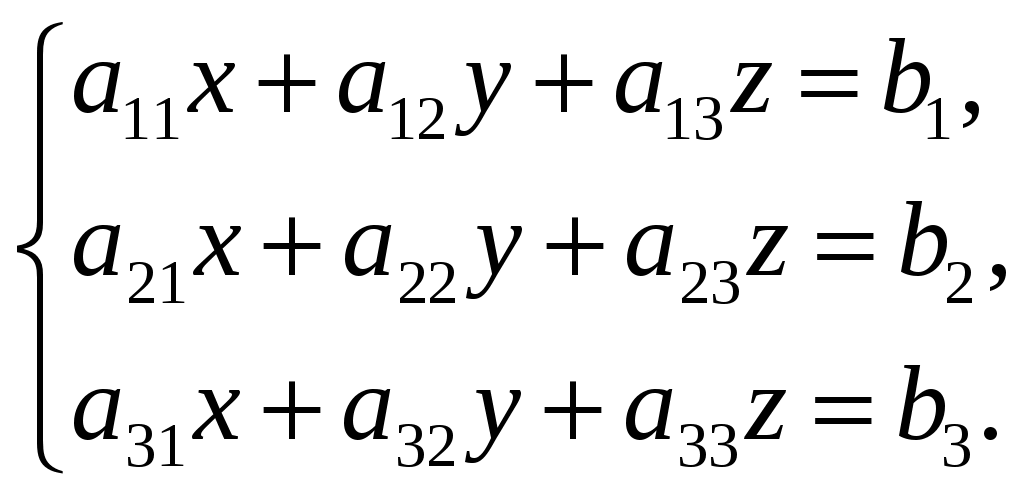
правило Крамера имеет вид:
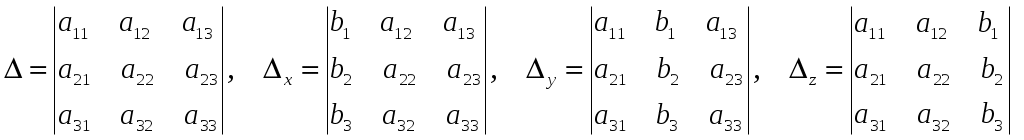 .
.Определитель третьего порядка, обозначаемый символом
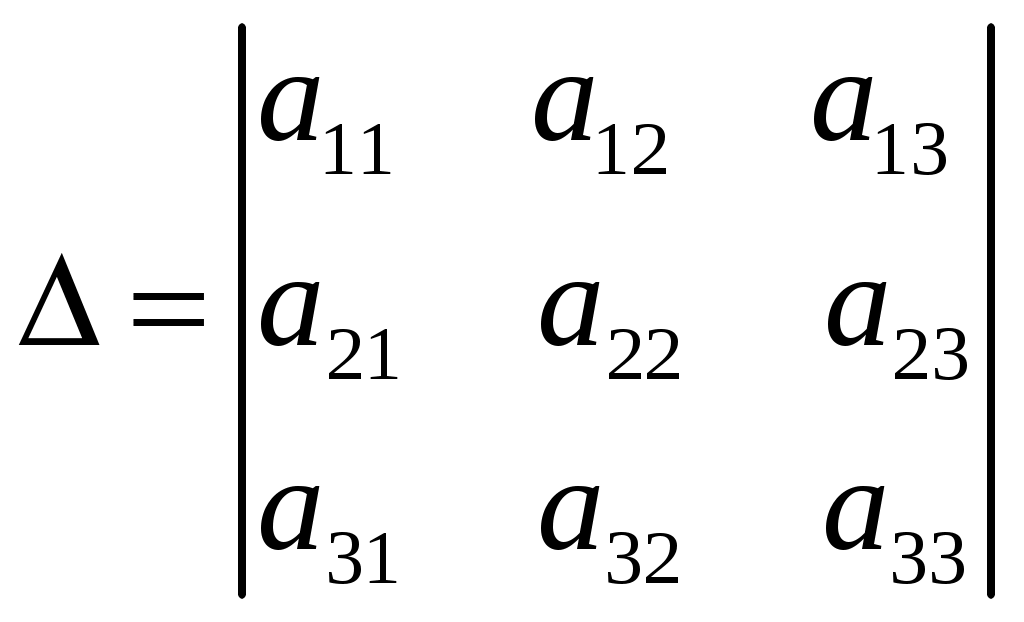 ,
,вычисляется по правилу треугольника или Сариуса:
Например
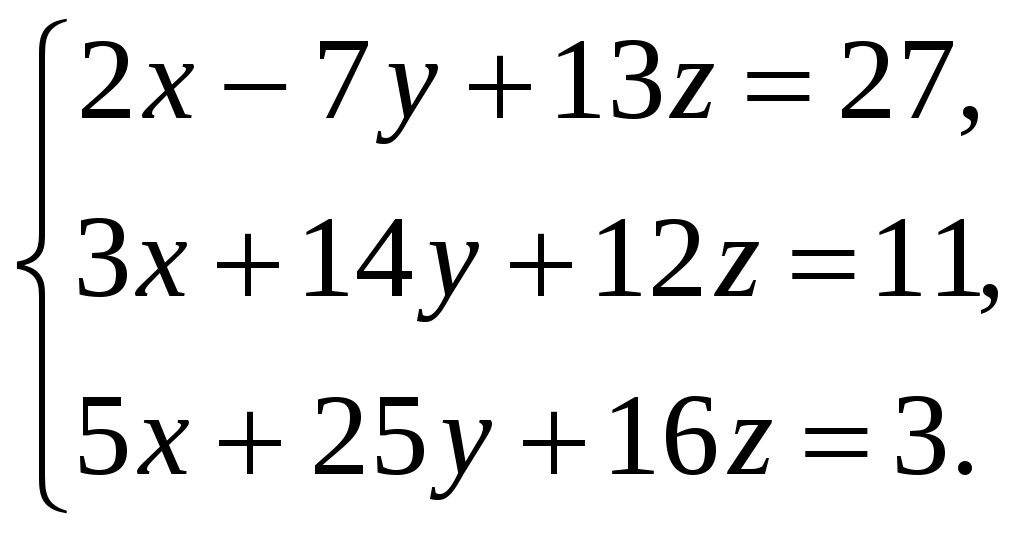
Решение.
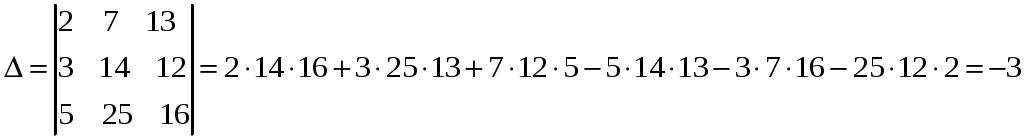
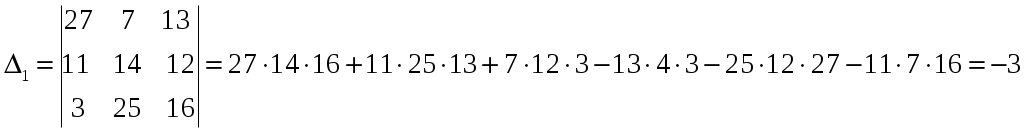
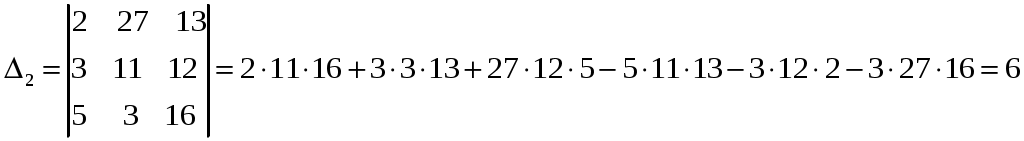
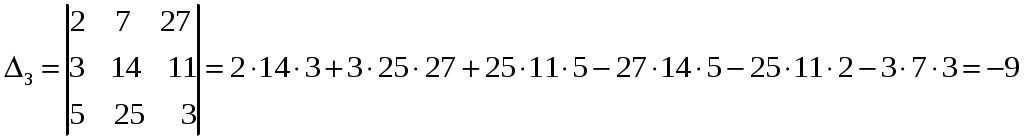
Ответ: (1, -2, 3).
Применение метода Гаусса приведено в примере к заданиям 1-10.
Задание № 5. Вычислить пределы функций, не пользуясь правилом Лопиталя.
При вычислении предела дробно-рациональной функции при
Пример 1.
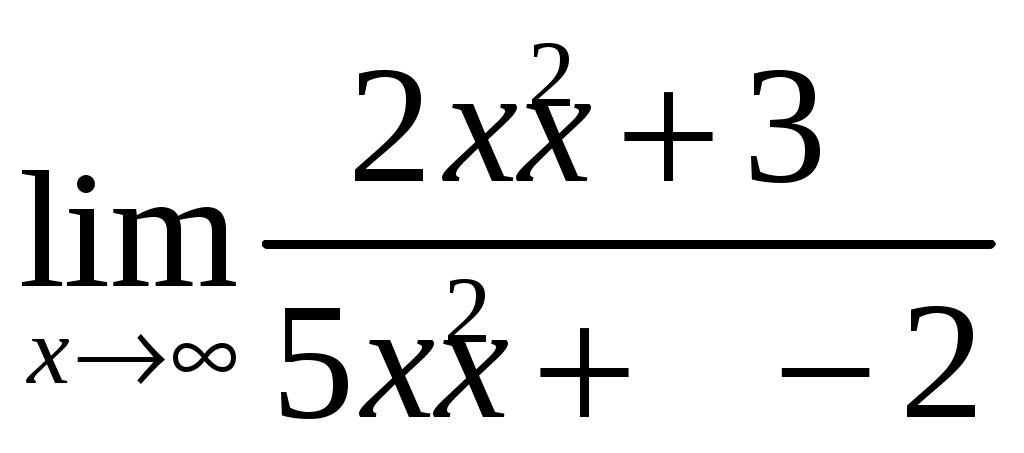 .
.Решение. Разделим числитель и знаменатель на степень
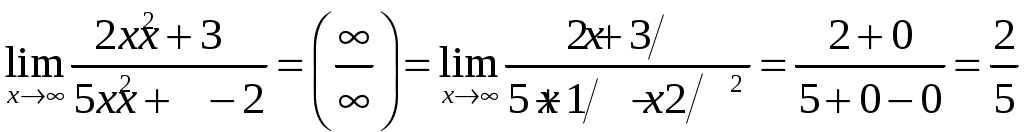 .
.В том случае, когда при вычислении предела дробно-рациональной функции при
Пример 2.
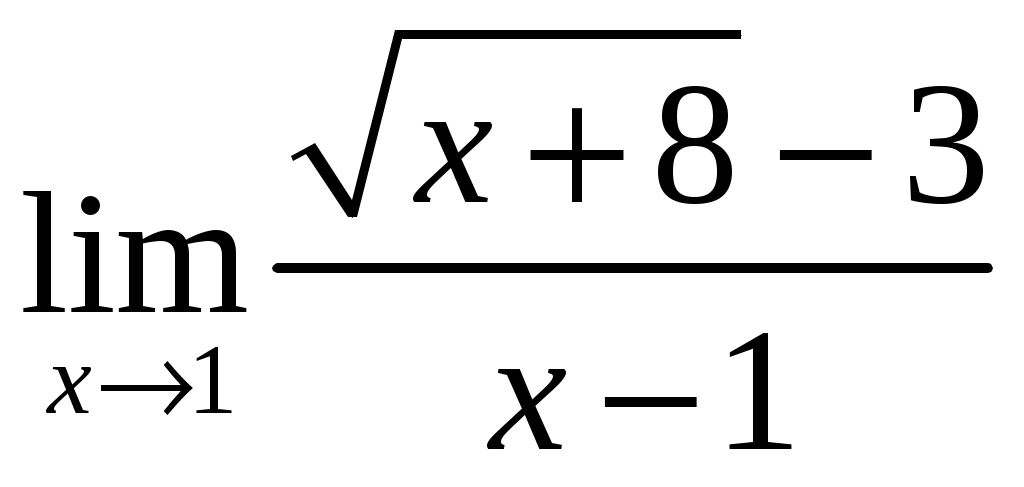 .
.Решение. Здесь мы имеем неопределенность вида
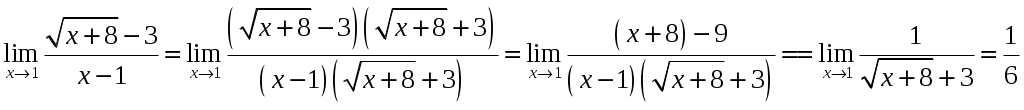 .
.При вычислении пределов тригонометрических функций часто используется первый замечательный предел и его следствия:
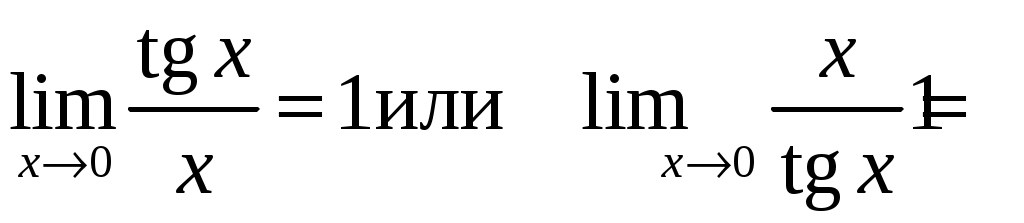 .
.Пример 3.
Решение. Преобразовав разность косинусов в произведение, получим
Если в пределе получаем неопределенность
второй замечательный предел.
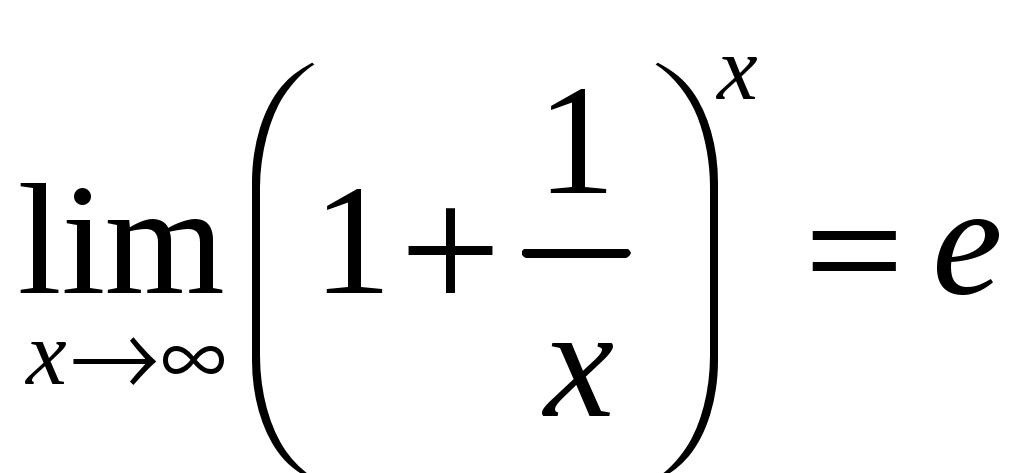 или
или Пример 4.
Решение. Выполнив преобразования и применив второй замечательный предел, найдём
Пример 5.
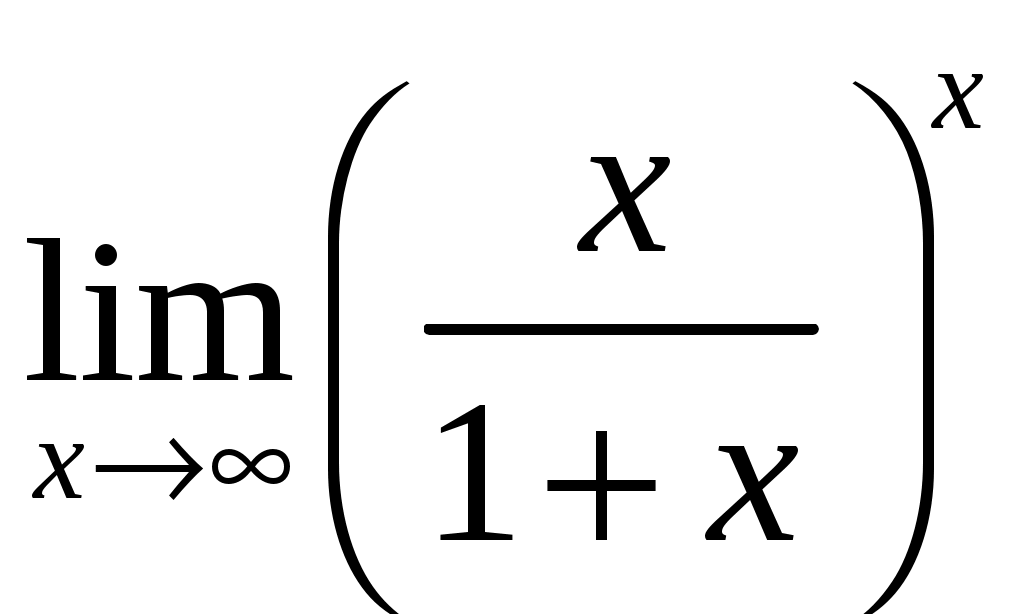 .
.Решение. Выполнив преобразования и применив формулу (2), найдём
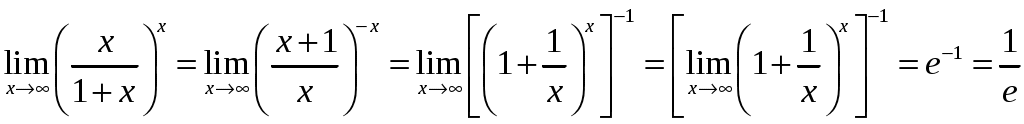 .
.Задание №6. Задана функция
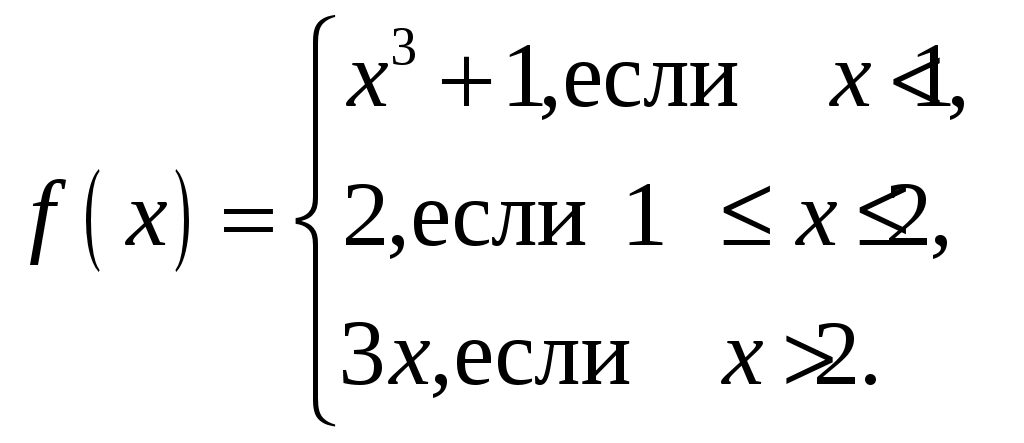
Решение. Функции
В точке
Таким образом,
.
В точке
Таким образом,

При выполнении следующего задания необходимо знать правила вычисления производной (производная суммы, произведения и частного дух функций), а также изучить таблицу производных.
Задание №7. Найти производные
а)
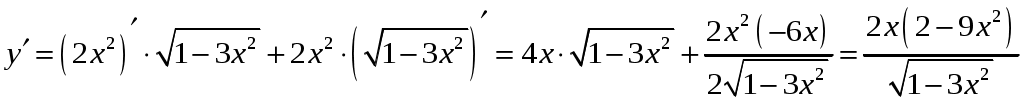 .
.б)
в)
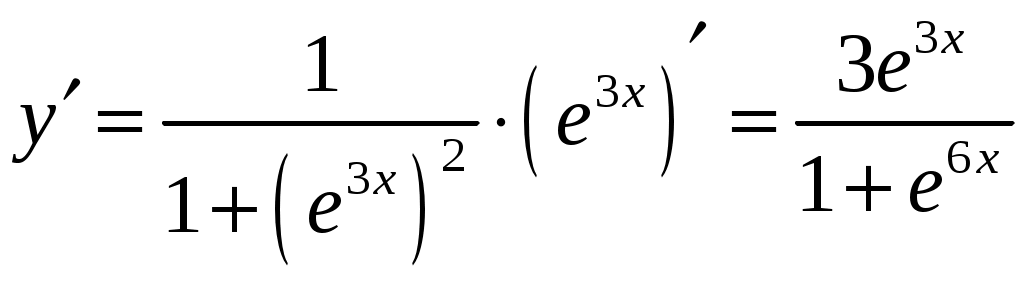 .
.г)
Прологарифмируем обе части равенства
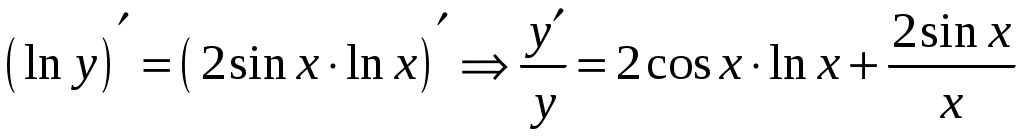 Откуда получаем
Откуда получаем 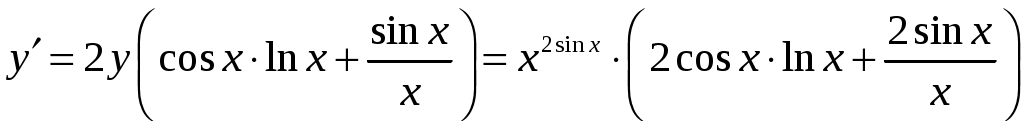 .
.д)
Продифференцируем обе части уравнения по x, учитывая, что y есть функция от x. Тогда получим
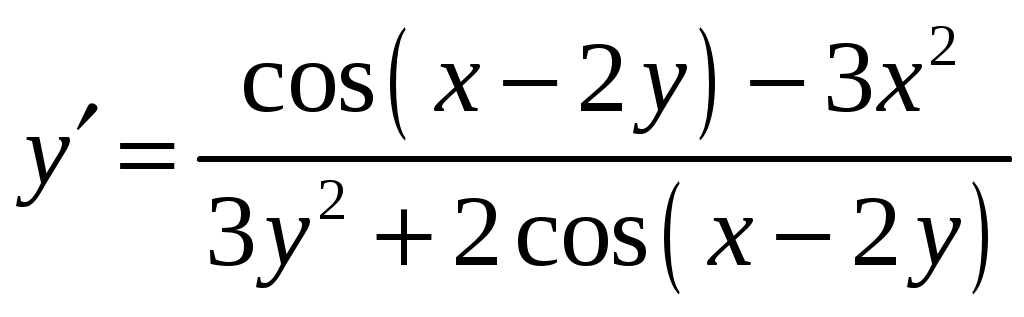 .
.Задание №8. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции
Решение. Разложим
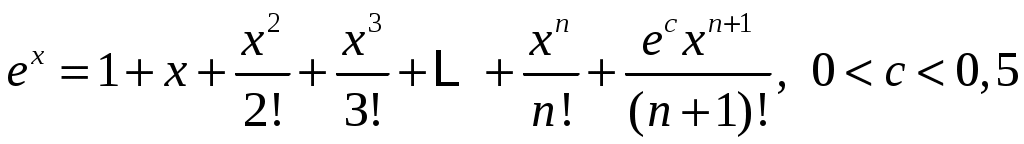 .
.Положив