Файл: Методические указания по изучению дисциплины и выполнению контрольных работ для студентов заочной формы обучения направлений.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 130
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6 Задания на контрольные работы
6.1 Контрольная работа №1 (Семестр 1)
Задание №1. По координатам вершин пирамиды
-
длину ребер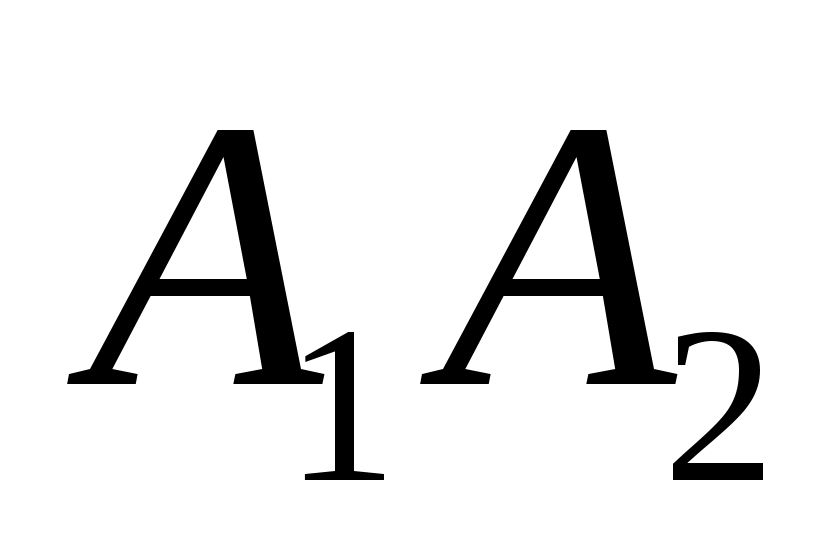 ,
, 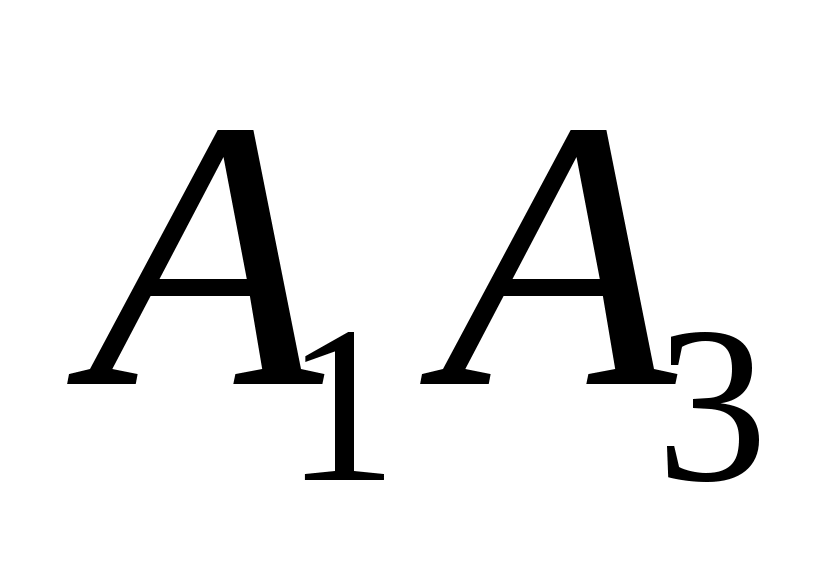 ;
; -
угол между ребрами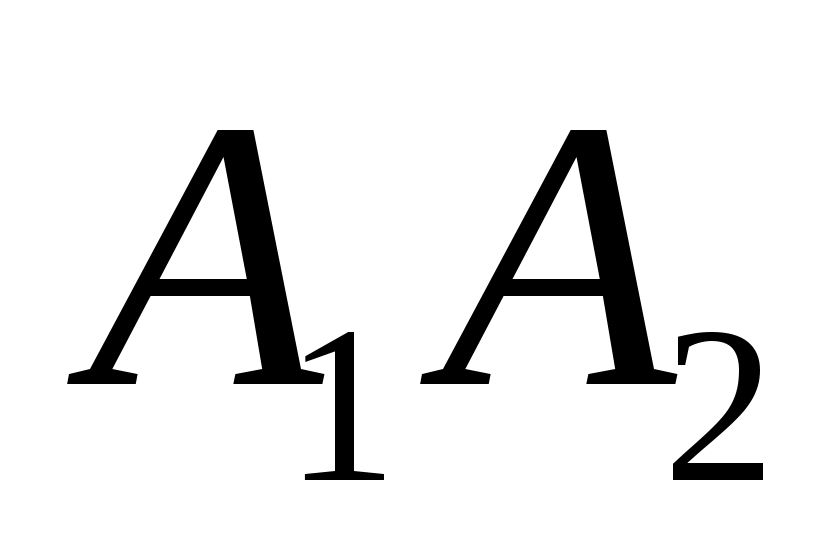 и
и 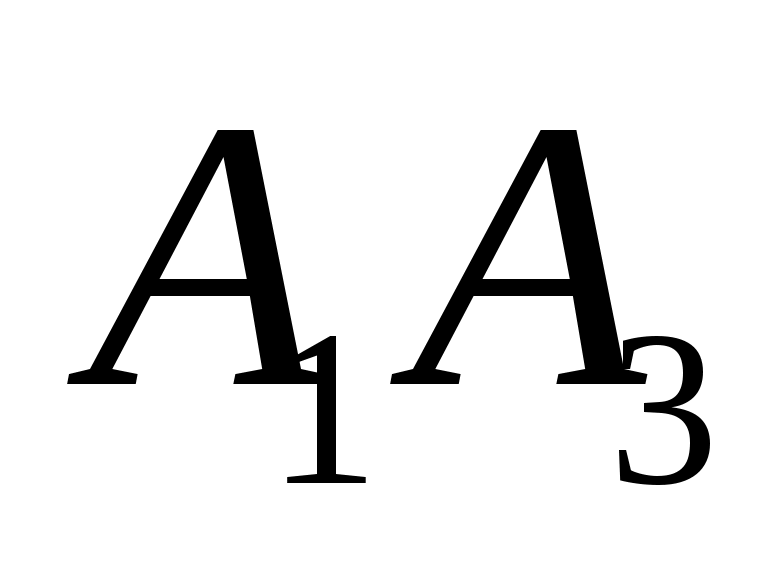 ;
; -
площадь грани ;
; -
объем пирамиды; -
уравнение прямой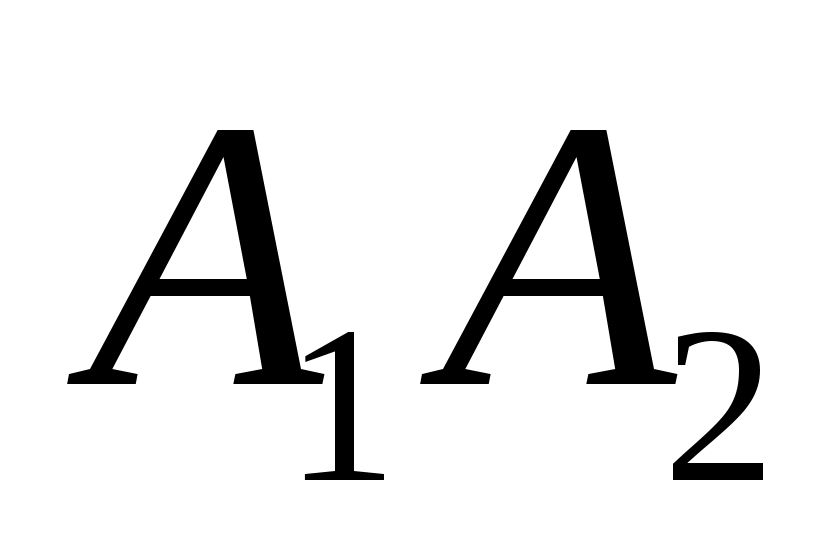 и
и 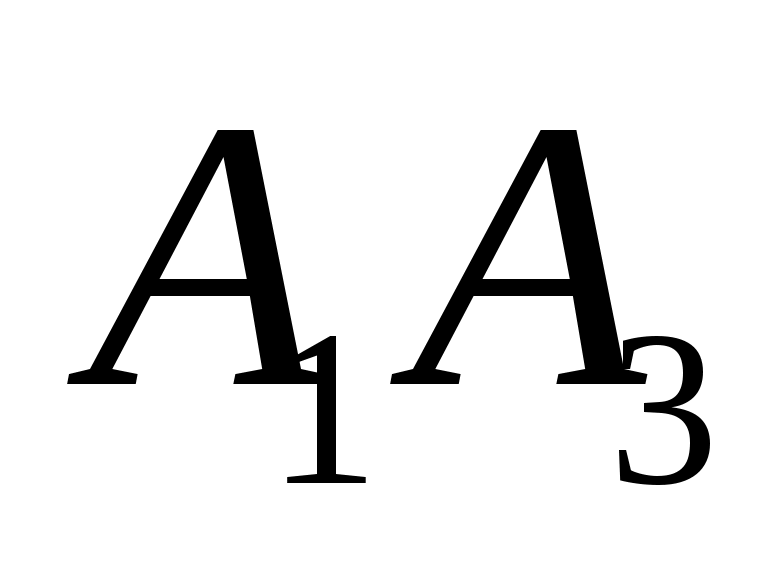 ;
; -
уравнение плоскости и
и 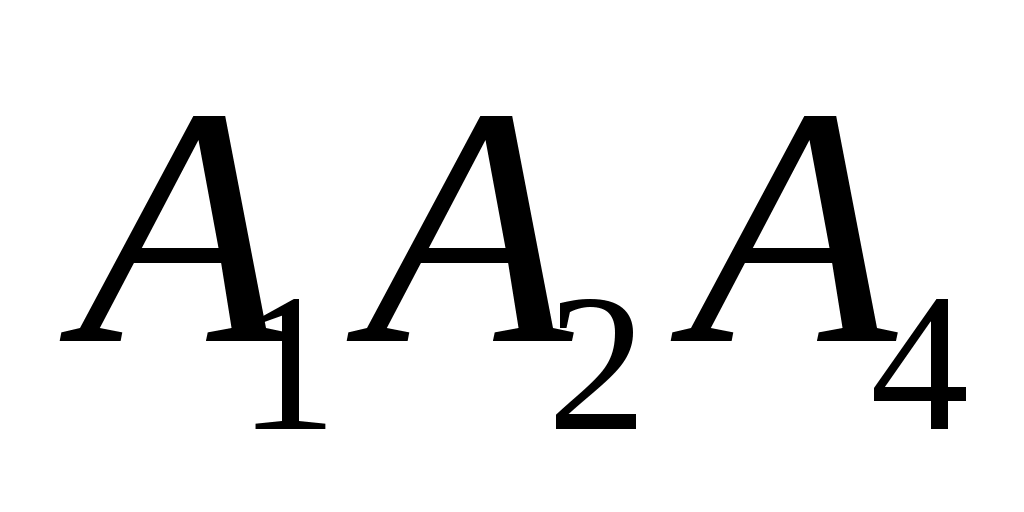 ;
; -
угол между плоскостями и
и 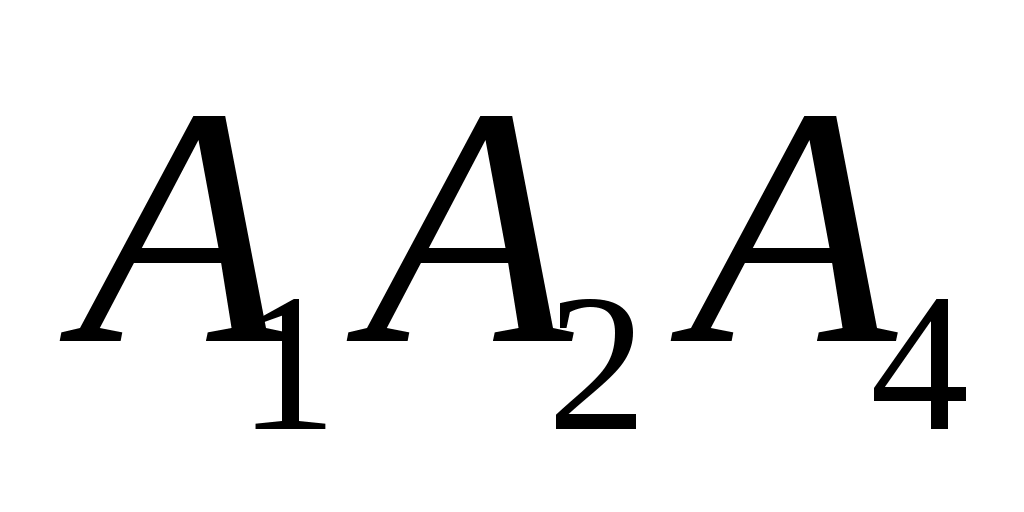 .
.
| Номер задачи | Координаты точки A1 | Координаты точки A2 | Координаты точки A3 | Координаты точки A4 |
| 1 | (0, 3, 2) | (-1, 3, 6) | (-2, 4, 2) | (0, 5, 4) |
| 2 | (-1, 2, 0) | (-2, 2, 4) | (-3, 3, 0) | (-1, 4, 2) |
| 3 | (2, 2, 3) | (1, 2, 7) | (0, 3, 3) | (2, 4, 5) |
| 4 | (0, -1, 2) | (-1, -1, 6) | (-2, 0, 2) | (0, 1, 4) |
| 5 | (3, 0, 2) | (2, 0, 6) | (1, 1, 2) | (3, 2, 4) |
| 6 | (0, 2,-1) | (-1, 2, 3) | (-2, 3, -1) | (0, 4, 1) |
| 7 | (2, 3, 2) | (1, 3, 6) | (0, 4, 2) | (2, 5, 4) |
| 8 | (-1, 0, 2) | (-2, 0, 6) | (-3, 1, 2) | (-1, 2, 4) |
| 9 | (2, 0, 3) | (1, 0, 7) | (0, 1, 3) | (2, 2, 5) |
| 10 | (2, -1, 2) | (1, -1, 6) | (0, 0, 2) | (2, 1, 4) |
Задание №2. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
-
найти ее решение с помощью формул Крамера; -
записать систему матричной форме и решить ее средствами матричного исчисления, при этом точность вычисления обратной матрицы проверить, используя матричное решение.
| 1. 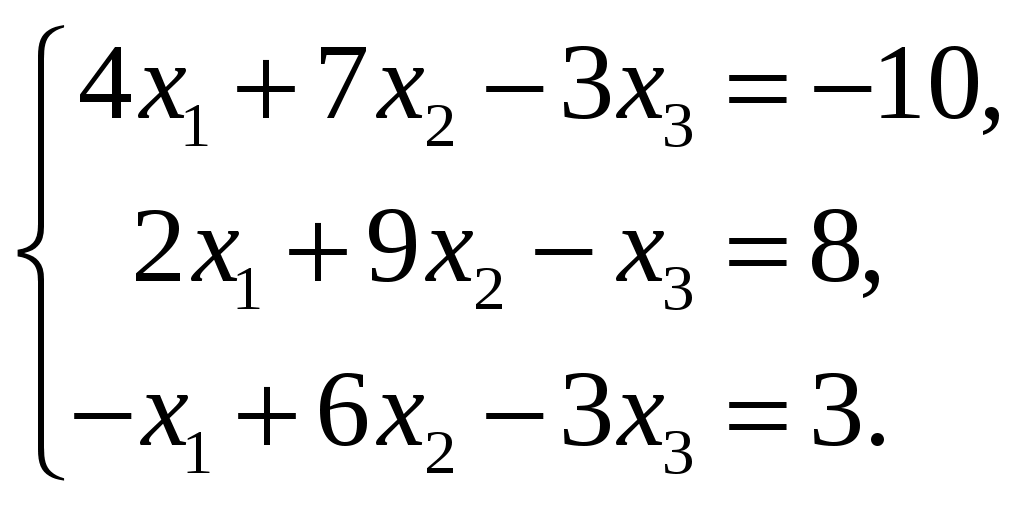 3. 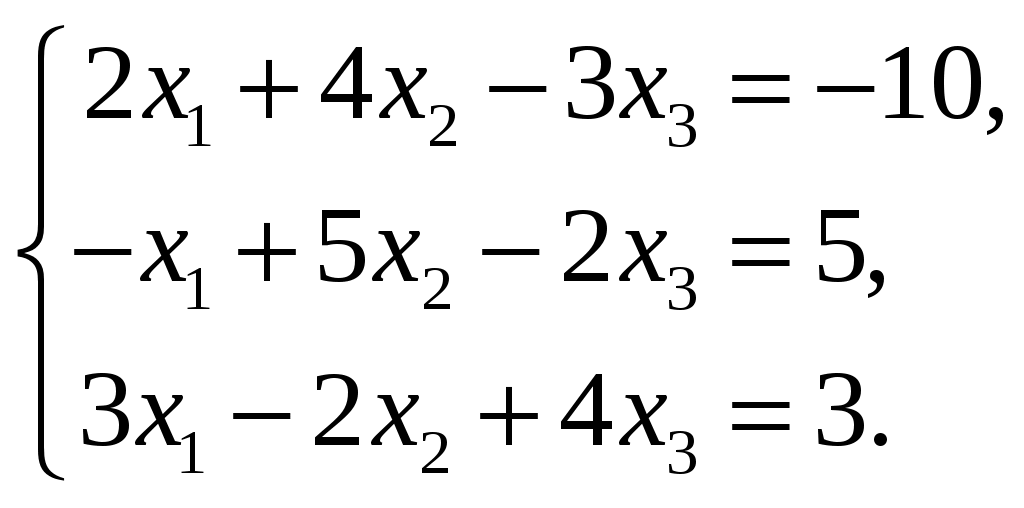 5. 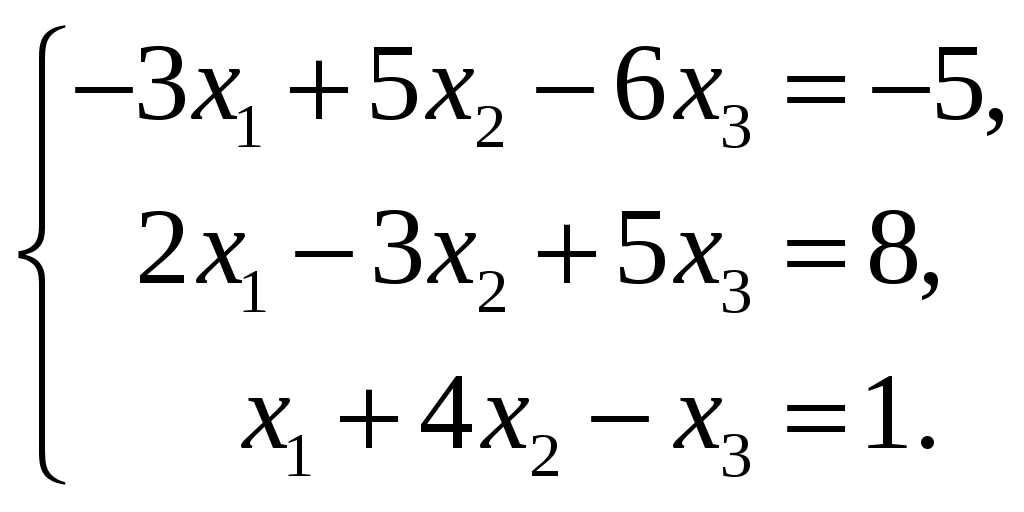 7.  9. 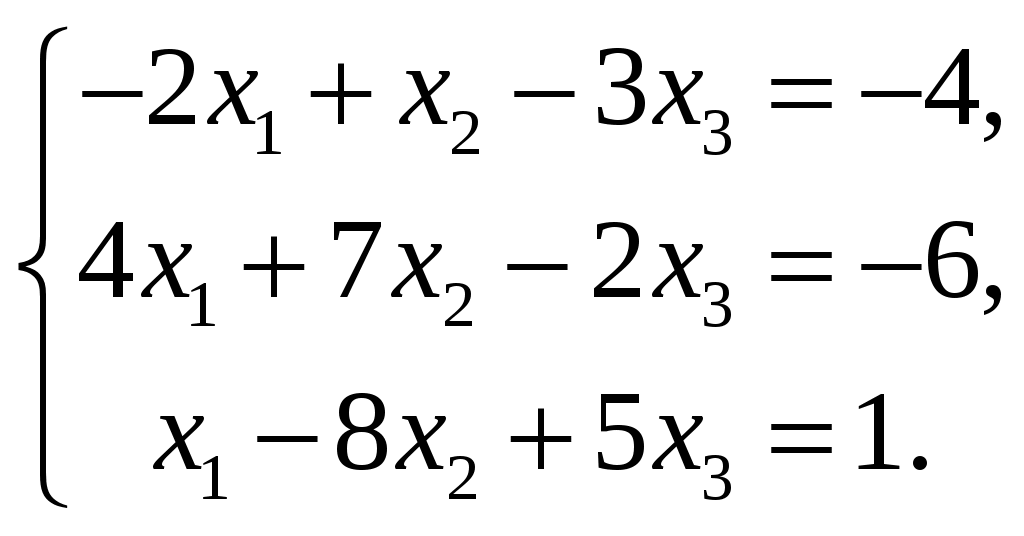 | 2. 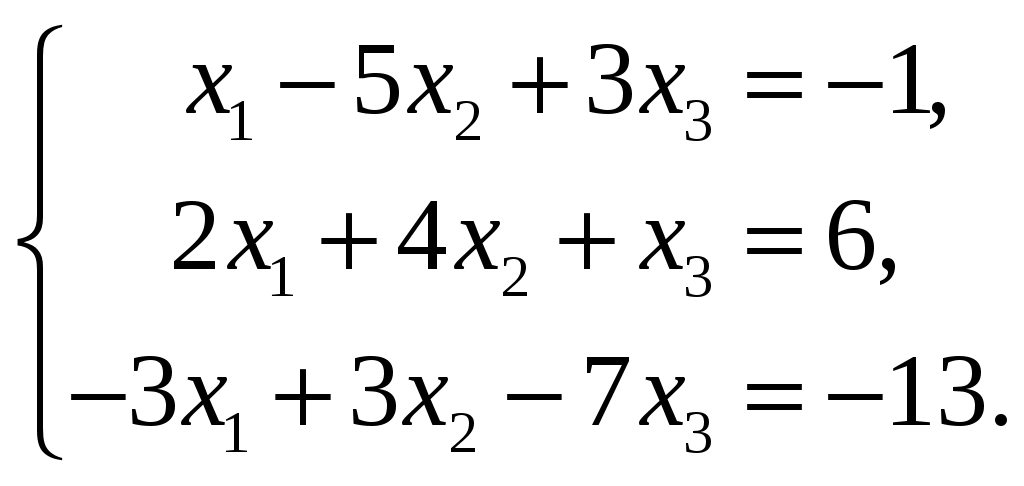 4.  6.  8. 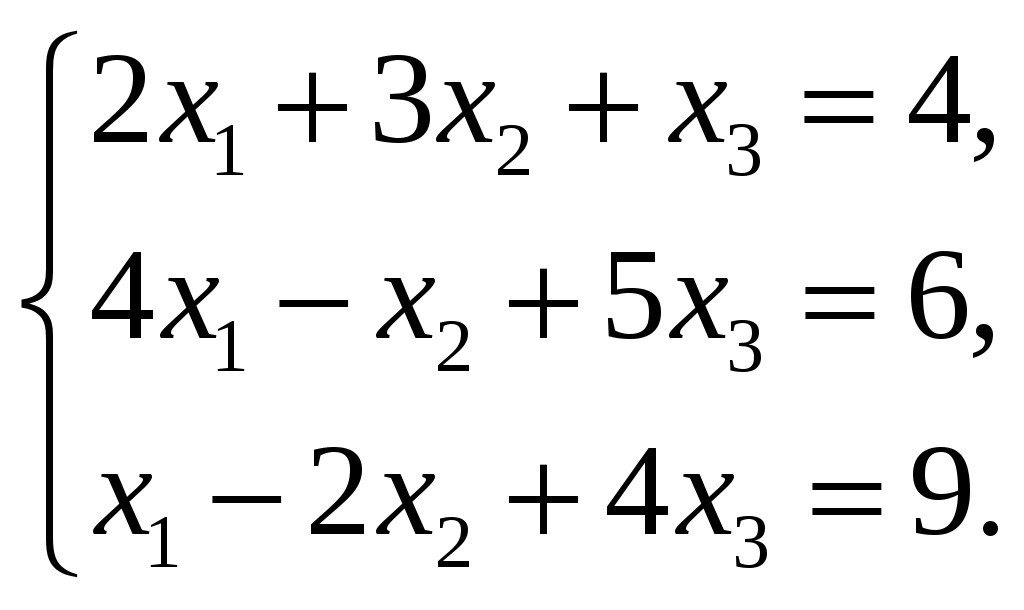 10. 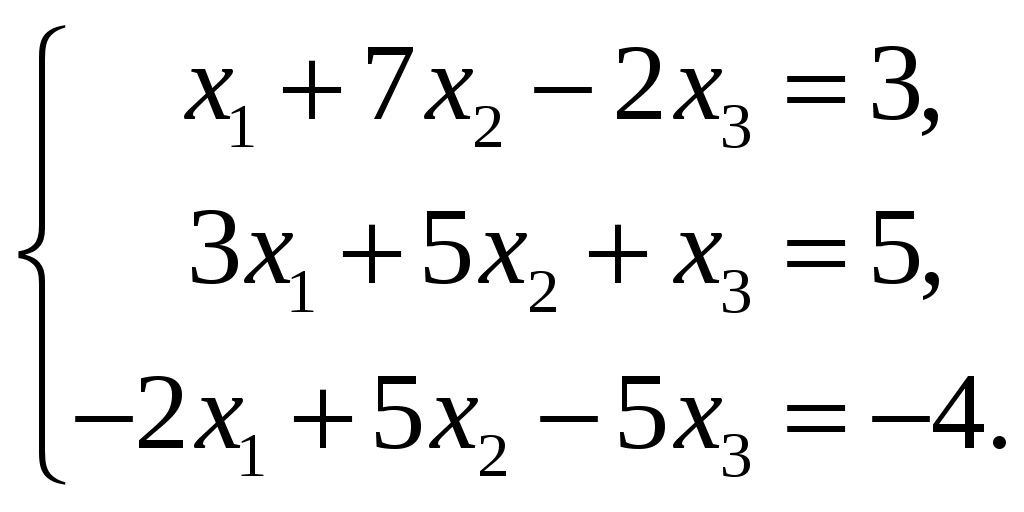 |
Задание №3. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1.1)
2.1)
3.1)
; 4)
4.1)
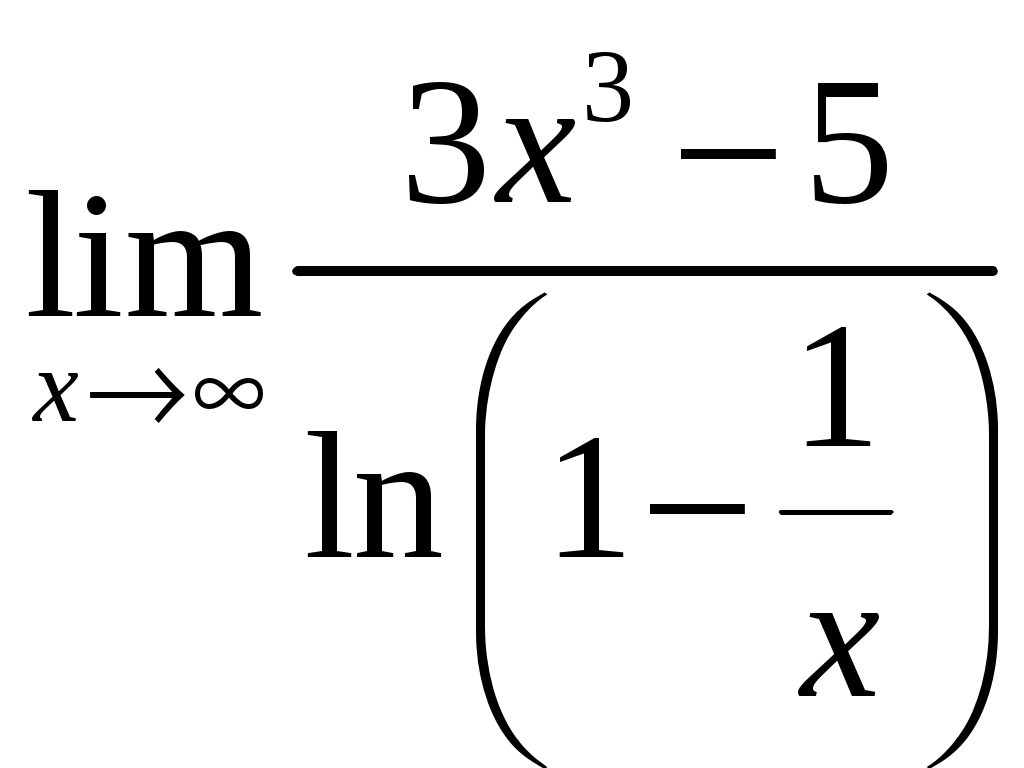 ; 2);
; 2); 5.1)
6.1)
7.1)
8.1)
9.1)
10.a)
; 4)
Задание №4. Функция f(x)представляет собой сумму одночленов. Указать среди них одночлен, эквивалентный функции f(x): а)при х→0; б) при х→∞;
| 1. | 2. |
| 3. | 4. |
| 5. | 6. |
| 7. | 8. |
| 9. | 10. |
Задание №5. Исследовать функцию
| 1.  3.  5. 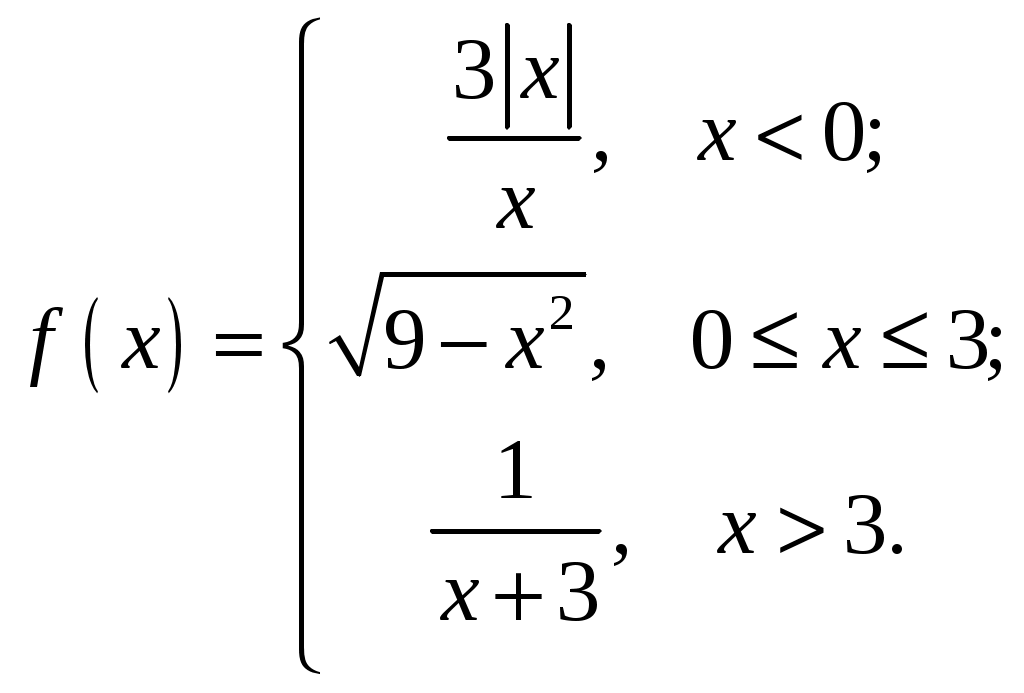 7. 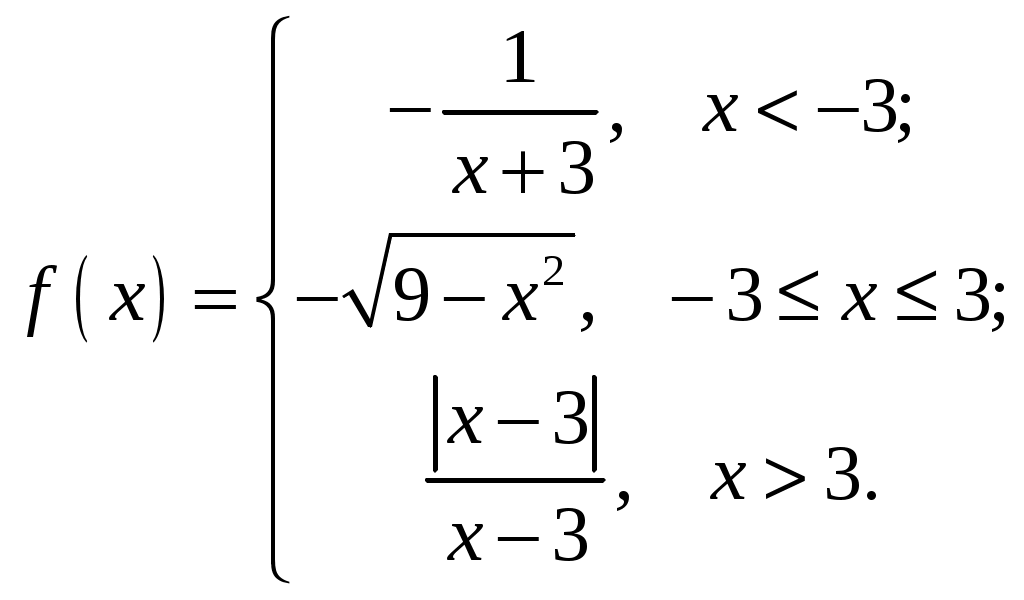 9. 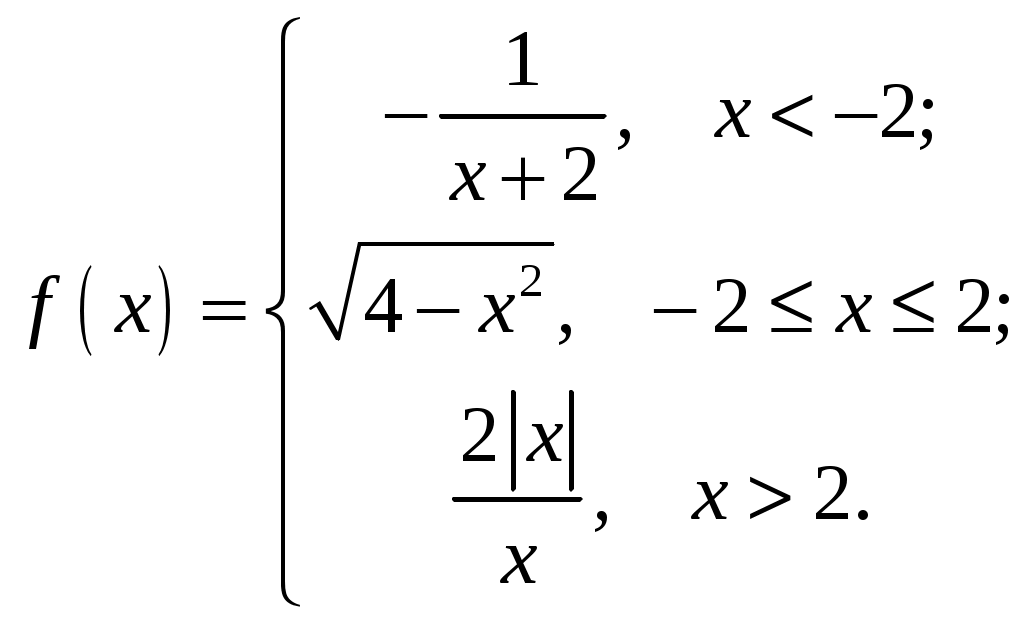 | 2. 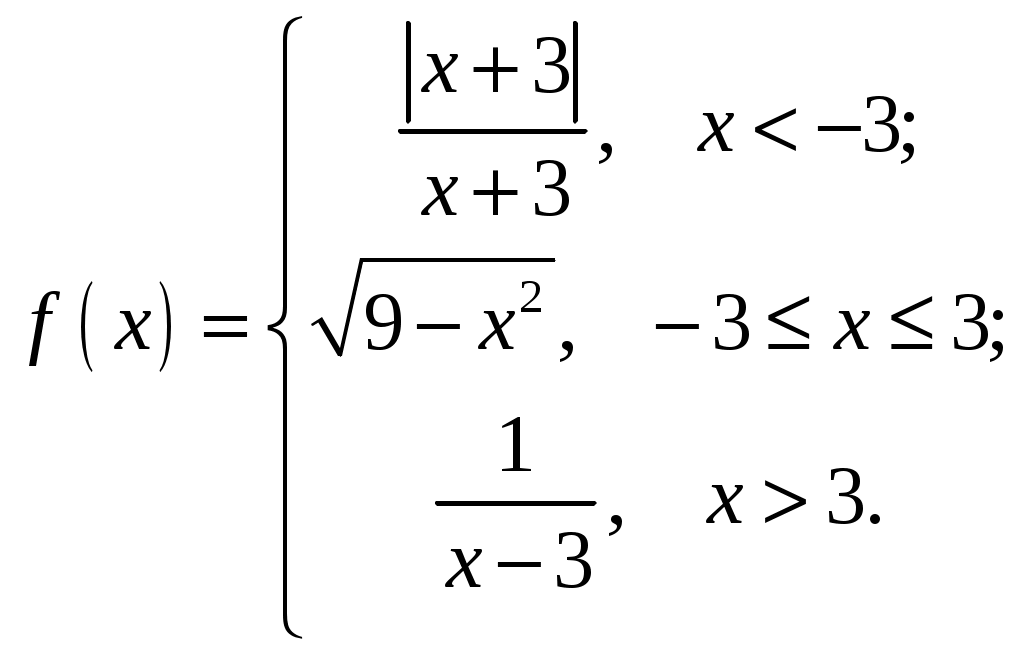 4. 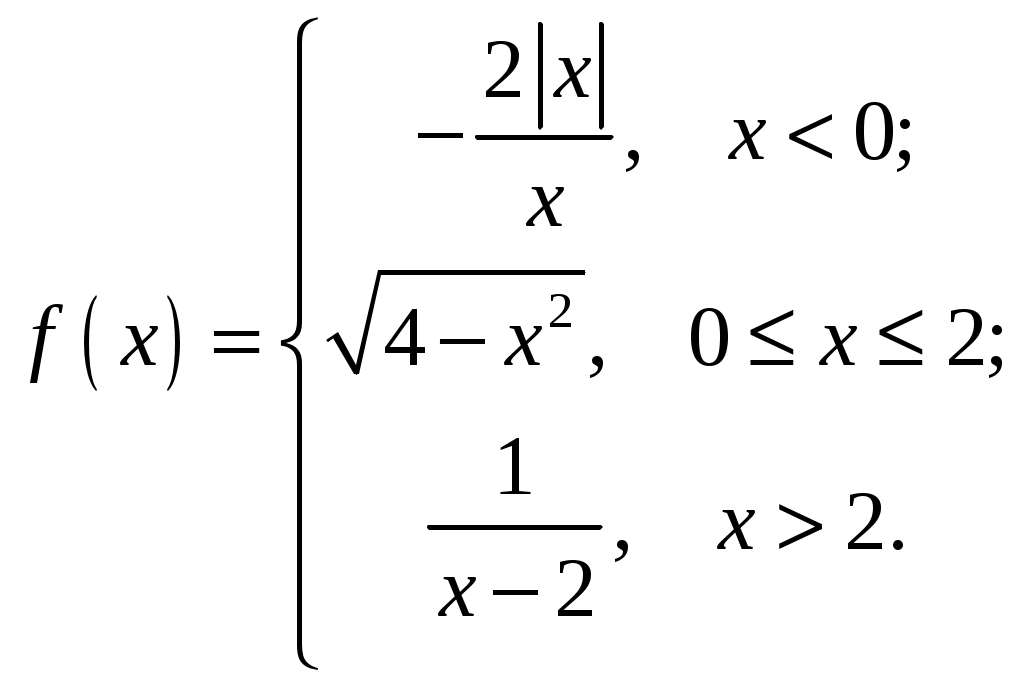 6.  8.  10.  |
Задание №6. Найти производные первого порядка данных функций, используя правила вычисления производных.
| | 1) | 2) | 3) | 4) 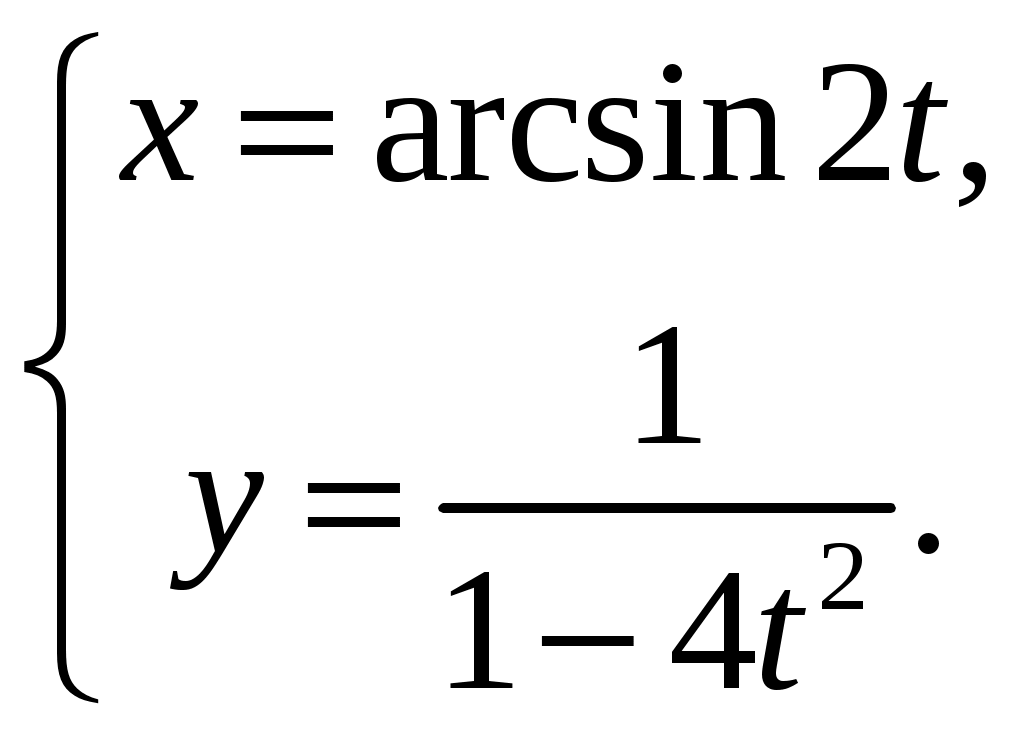 . . | ||
| | 1) | 2) | 3)  , , | 4) 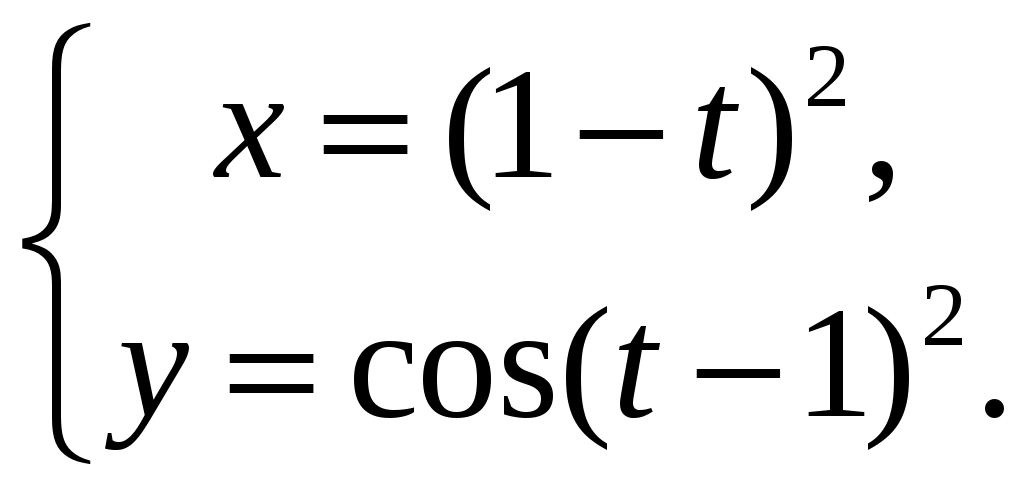 | ||
| | 1) | 2) | 3) | 4) 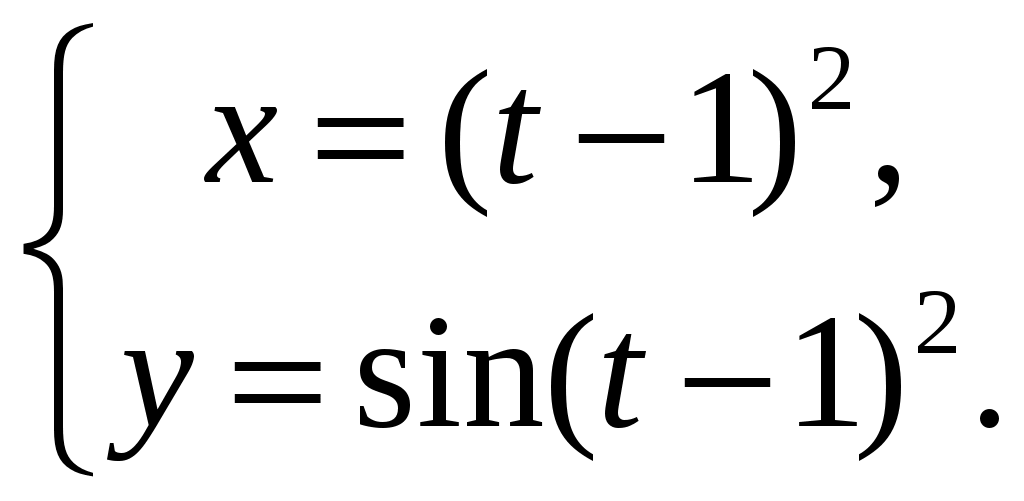 | ||
| | 1) | 2) | 3) 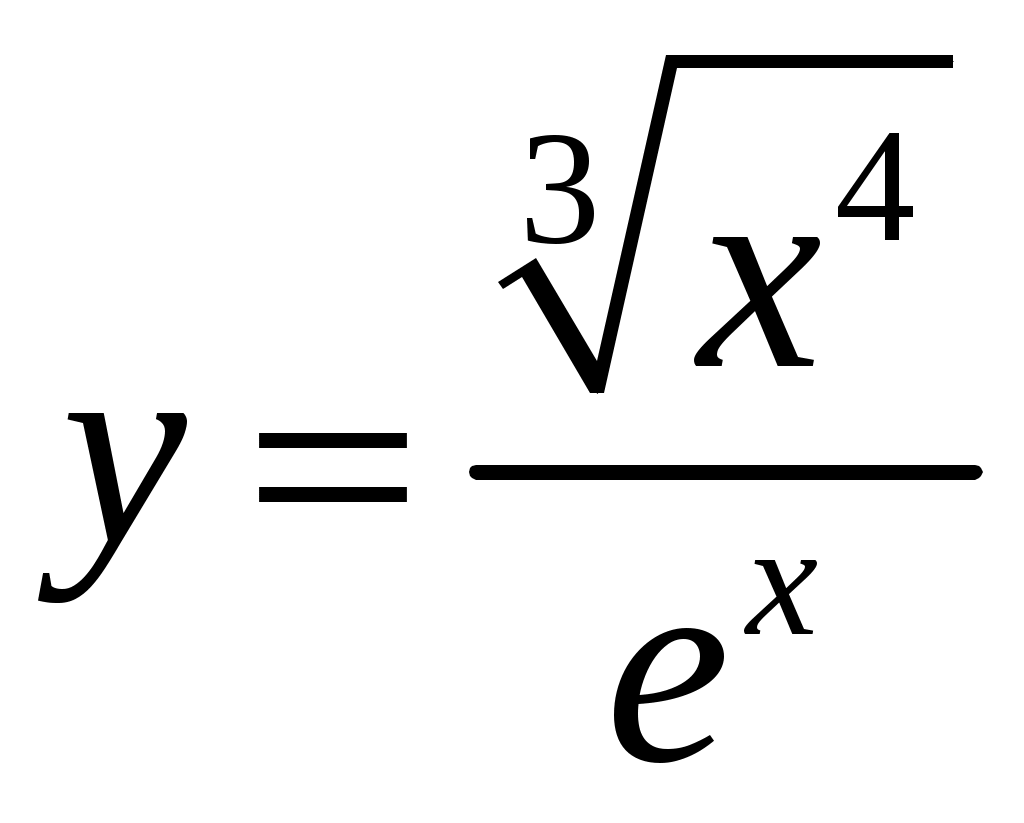 , , | 4) 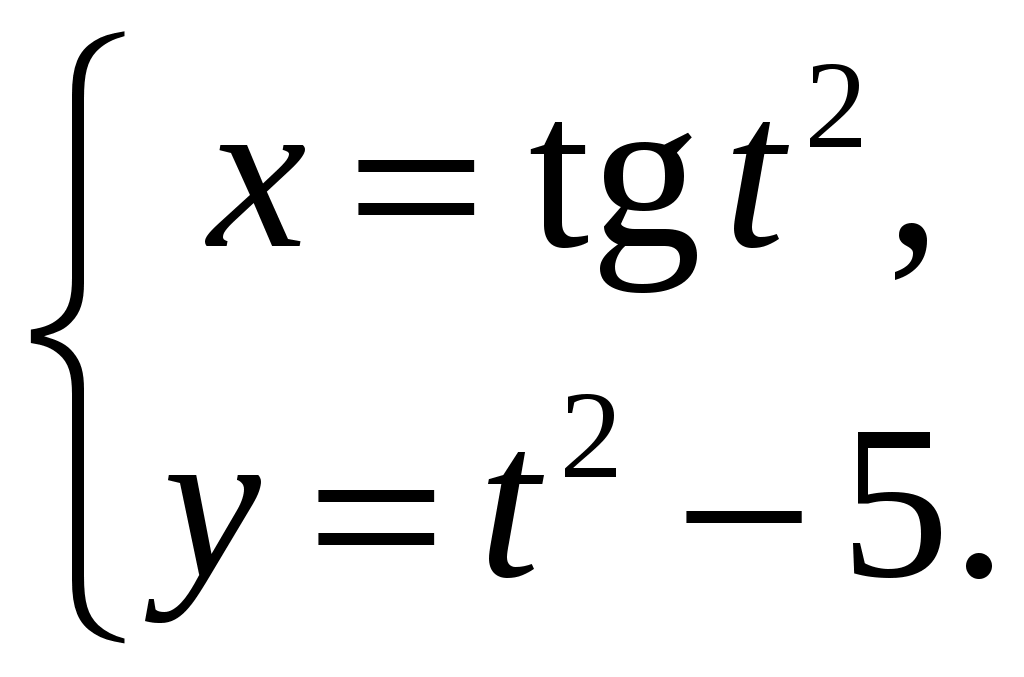 . . | ||
| | 1) | 2) | 3) | 4)  . . | ||
| | 1) | 2) | 3) | 4)  | ||
| | 1) | 2) | 3) | 4) 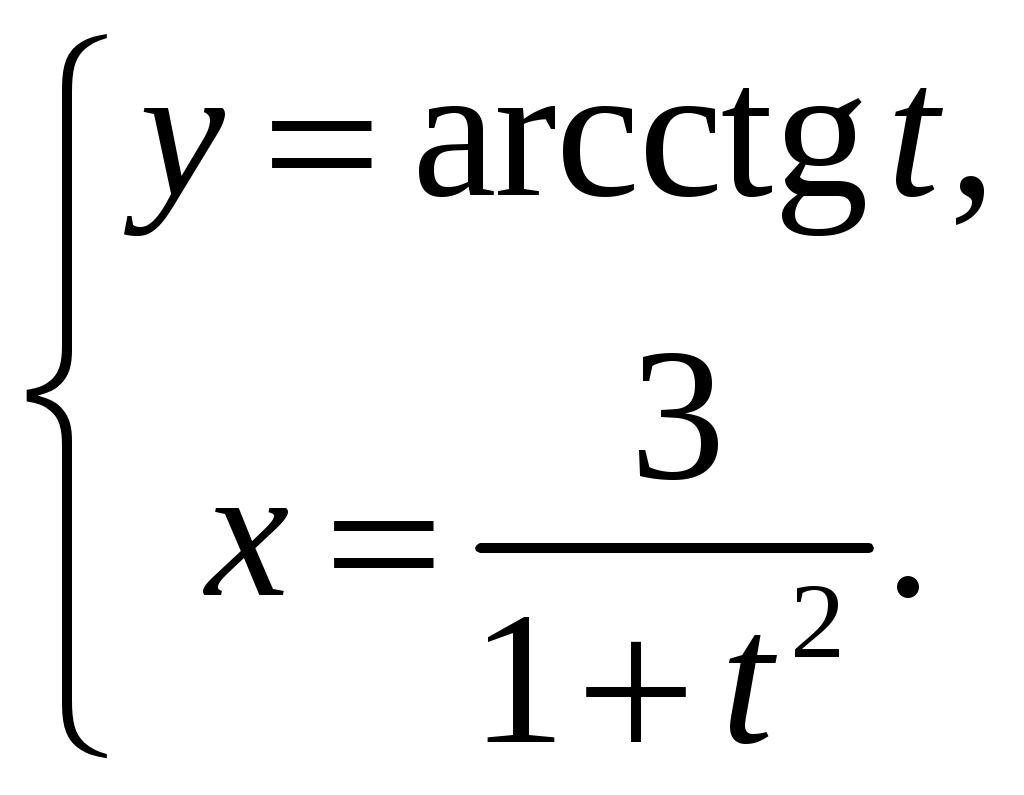 | ||
| | 1) | 2) | 3) | 4) 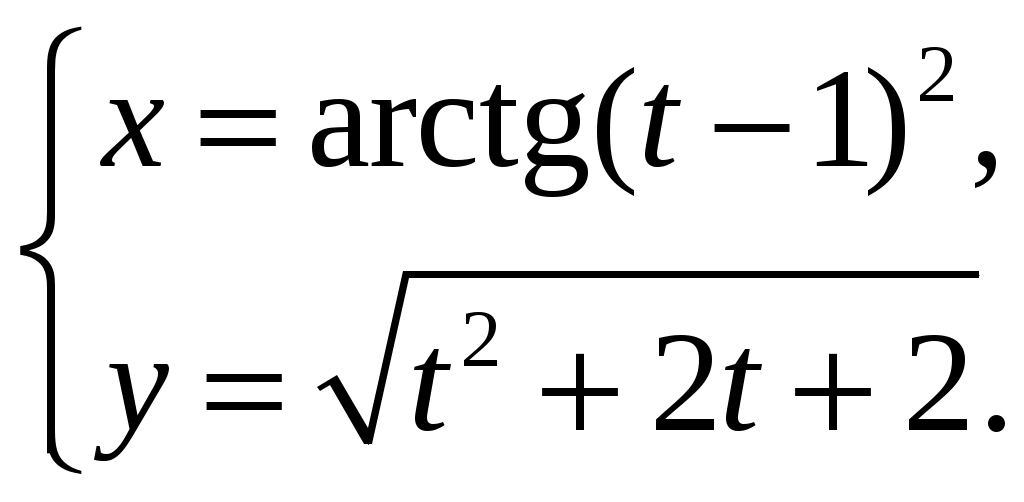 | ||
| | 1) | 2) | 3) | 4)  | ||
| | 1) | 2) | 3) | 4) 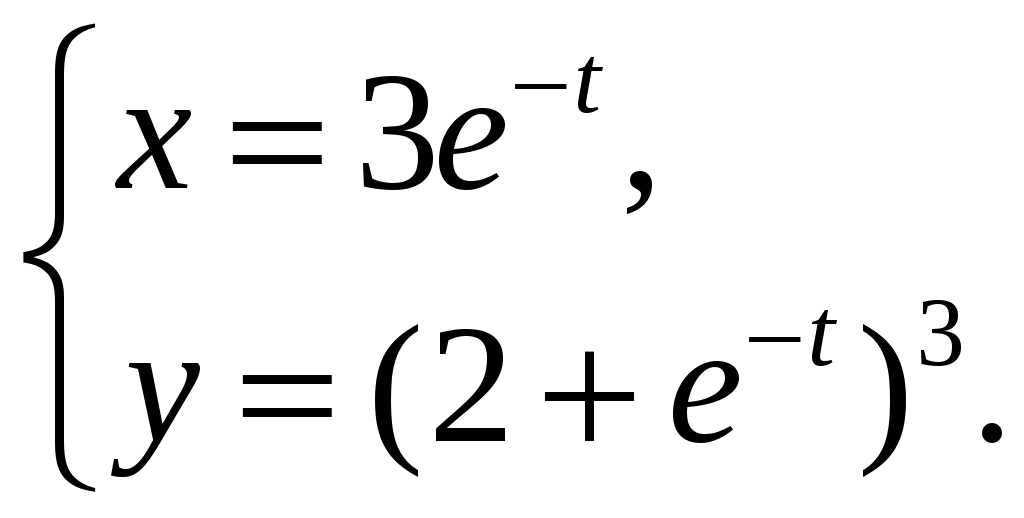 | ||
| | | | ||||