ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 420
Скачиваний: 3
СОДЕРЖАНИЕ
Практические задания …………………………………………. 14
Практические задания …………………………………………. 39
Практические задания …………………………………………. 58
Практические задания …………………………………………. 73
Практические задания …………………………………………... 88
Практические задания ………………………………………….. 99
Практические задания …………………………………………. 112
Практические задания …………………………………………. 123
– потребитель располагает ограниченным доходом (I), который весь расходует;
– потребитель рационален, т. е. стремится максимизировать полезность;
– цены благ (P) заданы и не зависят от количеств (Q), потребляемых отдельным потребителем;
I закон Госсена позволяет дать следующее определение:
II закон Госсена (условие равновесия потребителя в количественной теории полезности)
К особенностям потребительского выбора можно отнести
– эффект присоединения к большинству;
где – угол, образованный касательной к графику ТP и осью F;
Примеры решения задач
Задача 1
При цене билета в кинотеатр 5 ден. ед. его посетило 40 тыс. человек в течение месяца. Когда цена билета поднялась до 10 ден. ед., число посетителей сократилось до 10 тыс. человек. Если считать функцию спроса на билеты линейной, то сколько человек придут в кинотеатр при цене билета 4 ден. ед.?
Решение
Данная задача может быть решена тремя способами. Рассмотрим подробно каждый из них.
Первый способ
Если функция спроса линейна, то она имеет вид:
QD = b – a · P.
Повышение цены на 5 ден. ед. (10 ден. ед. – 5 ден. ед.) привело к сокращению числа зрителей кинотеатра на 30 тыс. человек (10 тыс. человек – 40 тыс. человек).
Каждый дополнительный рубль за билет сокращает число посетителей на 6 тыс. человек (–30 000 / +5), поэтому коэффициент "а" в уравнении функции спроса равен (–6 000).
Теперь можно найти свободный член уравнения для любой пары переменных:
40 000 = b – 6 000 · 5 = b – 30 000;
b = 70 000.
Функция спроса имеет следующий вид:
QD = 70 000 – 6 000 · P.
Следовательно, при цене билета 4 ден. ед. в кинотеатр придут 46 тыс. зрителей (70 000 – 6 000 · 4).
Второй способ
Воспользуемся формулой определения уравнения прямой линии по двум точкам:
А (Х1; Y1) и Б (Х2; Y2);
В данном случае координаты точек таковы:
А (5; 40 000) и Б (10; 10 000).
Следовательно,
QD = 70 000 – 6 000 · P.
Подставив в полученное уравнение значение новой цены билета Р = 4 ден. ед., получаем аналогичный результат: QD = 46 000 человек.
Третий способ
С
 оставим и решим систему линейных уравнений вида y = аx + b с двумя неизвестными коэффициентами а и b уравнения прямой; x – цена билета; y – соответствующая величина спроса:
оставим и решим систему линейных уравнений вида y = аx + b с двумя неизвестными коэффициентами а и b уравнения прямой; x – цена билета; y – соответствующая величина спроса:40 000 = а · 5 + b, b = 40 000 – 5а,
10 000 = а · 10 + b; 10 000 = 10а + b;
b = 40 000 – 5а,
10 000 = 10а + 40 000 – 5а.
а = – 6 000, b = 70 000.
Получаем аналогичное уравнение функции спроса и тот же результат:
QD
= 70 000 – 6 000 · P; при Р = 4 ден. ед.
QD = 46 тыс. человек.
Задача 2
Функция спроса на товар имеет вид: QD = 16 – 2P, функция предложения данного товара: QS = –8 + 4P. Что произойдет на рынке в каждом из этих случаев?:
а) на товар введён налог, уплачиваемый продавцом, в размере 1 ден. ед. на единицу товара;
б) правительство ввело дотацию в 2 ден. ед., получаемую продавцом за каждую единицу продукции;
в) правительство установило фиксированную цену в 5 ден. ед. на данный товар.
Решение
Равновесие на рынке предполагает равенство спроса и предложения, следовательно:
QD = QS;
16 – 2P = – 8 + 4P;
Р = 4 ден. ед.
При этом QD = QS = 8 ед.
А. Введение налога уменьшает доход продавца с единицы продукции, следовательно, функция предложения примет вид:
QS = –8 + 4 (P – 1) = – 12 + 4Р.
Тогда равновесная цена составит
16 – 2P = –12 + 4Р;
Р = 4,7 ден. ед.
При этом QD = QS = 16 – 2 · 4,7 = 6,6 ед.
В бюджет государства будет уплачено 6,6 ден. ед. налога (6,6 ед. · 1 ден. ед.).
Б. Введение дотации увеличивает реально получаемый продавцом доход с единицы товара, поэтому новое равновесие на рынке достигается при следующих условиях:
16 – 2P = –8 + 4 (P + 2);
Р = 2,7 ден. ед.
QD = QS = 16 – 2 · 2,7 = 10,6 ед.
В. Введение фиксированной цены выше равновесной приведёт к возникновению излишка товара. Первоначальная цена составляла 4 ден. ед. При цене 5 ден. ед. величина спроса будет равна:
16 – 2 · 5 = 6 ед.;
предложения:
– 8 + 4 · 5 = 12 ед.
Излишек составит 6 ед.
Задача 3
В табл. 11, 12 приведена информация о ценах и спросе на продукты. Определите коэффициенты перекрёстной эластичности. Объясните, как изменяются эти коэффициенты в зависимости от того, являются ли товары взаимозаменяемыми или взаимодополняемыми.
Таблица 11
Информация о ценах и спросе на масло и маргарин
| Цена масла, руб. | Спрос на масло, кг | Цена маргарина, руб. | Спрос на маргарин, кг |
| 190 | 10000 | 45 | 12500 |
| 180 | 13000 | 50 | 11000 |
| 170 | 17000 | 55 | 8500 |
| 160 | 22000 | 60 | 6500 |
| 150 | 25000 | 65 | 5000 |
Таблица 12
Средняя цена на фотоаппараты и спрос на фотоплёнку
| Средняя цена одного фотоаппарата, руб. | Спрос на фотоплёнку, м |
| 2000 | 100000 |
| 3000 | 95000 |
| 4000 | 90000 |
| 5000 | 85000 |
| 7000 | 70000 |
| 8000 | 60000 |
Решение
Масло и маргарин являются типичными товарами-заменителями. Чтобы подтвердить это предположение, рассчитаем коэффициенты перекрёстной эластичности спроса на маргарин по цене масла. Коэффициент эластичности в данном случае должны быть больше нуля:
Фотоплёнка и фотоаппарат – типичные взаимодополняемые товары. Коэффициент перекрёстной эластичности должен быть меньше нуля:
Задача 4
Рассчитайте коэффициенты эластичности спроса по цене по следующим данным: при цене единицы товара 6,3 тыс. руб. объём продаж равен 1000 шт., при цене 5,4 тыс. руб. он составил 1800 шт., при цене 4,6 тыс. руб. – 2800 шт., при цене 3,5 тыс. руб. – 3700 шт., при цене 2,7 тыс. руб. – 4500 шт., при цене 1,8 – 5400 шт. Сделайте вывод о характере спроса, определите оптимальный уровень цен и объём продаж.
Решение
Рассчитаем коэффициенты эластичности спроса по цене по формуле дуговой эластичности:
Чтобы определить оптимальный объём продаж и цену товара, необходимо рассчитать выручку от реализации и проанализировать коэффициенты эластичности спроса по цене. Как видно из табл. 13, наибольший объём реализации (в натуральном выражении) достигается при цене 1,8 тыс. руб., однако выручка при этом не является максимальной.
Таблица 13
| Объём продаж товара, шт. | Цена единицы товара, тыс. руб. | Выручка от продаж, тыс. руб. | Коэффициент эластичности спроса по цене (по модулю) |
| 1000 | 6,3 | 6300 | – |
| 1800 | 5,4 | 9720 | 3,7 |
| 2800 | 4,6 | 12880 | 2,7 |
| 3700 | 3,5 | 12950 | 1,0 |
| 4500 | 2,7 | 12150 | 0,8 |
| 5400 | 1,8 | 9720 | 0,5 |
Оптимальным будет тот объём продаж, который обеспечивает максимум денежных поступлений и при этом спрос на товар остаётся эластичным (коэффициент эластичности больше единицы по модулю). Исходя из этого, фирме следует назначить цену 3,5 тыс. руб., чтобы получить максимальную выручку в 12950 тыс. руб.
Задания для самостоятельной работы
Напишите реферат по теме:
Модели рыночной экономики: американская, японская, немецкая, шведская, французская, южно-корейская, китайская. Сравнительный анализ моделей.
Формирование российской рыночной системы.
Формы монополий и их эволюция.
Естественные монополии в России: история, перспективы развития и реформирования.
Дефицитный рынок: причины возникновения и последствия.
Экономический механизм спроса и предложения.
Как размер олигополии влияет на рыночный результат.
ТЕМА 3. ТЕОРИЯ СПРОСА
И ПОТРЕБИТЕЛЬСКОЕ ПОВЕДЕНИЕ
Теоретические основы для подготовки
к практическому занятию
Потребитель как агент экономической деятельности. Понятие "потребность". Материальные, духовные, социальные потребности потребителя. Предпочтения потребителя и полезность. Функция полезности. Понятие "потребительская корзина", индексы цен.
Поведение потребителя. Факторы, определяющие спрос потребителя: цена блага, доход потребителя, мода и др.
Объяснение поведения потребителя с помощью теории предельной полезности. Понятия "общая полезность", "предельная полезность". Закон убывающей предельной полезности. Правило потребительского поведения, "эффект дохода", "эффект замещения".
Объяснение поведения потребителя с помощью кривых безразличия. Карта кривых безразличия. Бюджетная линия. Пересечение бюджетной линии с кривой безразличия – условие равновесного положения потребителя. Кривая Энгеля.
Основные понятия, необходимые для изучения темы
Полезность (Utility) – уровень удовлетворения, получаемый при потреблении благ. Полезность определяется различными способами.
При количественном (кардиналистском) подходе к анализу полезности потребитель способен поставить в соответствие каждому набору благ получаемый уровень полезности (абсолютная шкала измерения). Тогда полезность измеряется в условных единицах (ютилах).
При порядковом (ординалистском) подходе к анализу полезности потребитель способен упорядочить все наборы по уровню получаемой полезности. Конкретное значение полезности, соответствующее потребительскому набору, не имеет значения (относительная шкала измерения). Тогда полезность не имеет единиц измерения.
Количественный подход оценки полезности позволяет вывести функцию полезности связывает множество факторов:
U = F(QA, QB, …, QZ),
где U – уровень полезности,
QA, QB, …, QZ – объёмы потребления в единицу времени благ A, B, … Z, соответственно (потребительский набор).
Общая полезность: TU(Q) (Total Utility) – общий уровень полезности, получаемый при потреблении некоторого количества благa Q.
Предельная полезность: MU (Marginal Utility) – прирост полезности, получаемый от потребления дополнительной (последней) единицы блага.
На рис. 16 графически представлена взаимосвязь общей и предельной полезностей от уровня потребления.
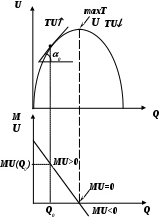
Для дискретно заданной или непрерывной и дифференцируемой функции TU(Q)