Файл: Отчеты оформляются в виде файлов формата Microsoft Word (файлы других форматов не принимаются), размер шрифта 1214.docx

Так называемая рабочая зона управляющей таблицы содержит только клетки с переходами (верхняя строка показанной таблицы не входит в рабочую зону). Если в рабочей зоне управляющей таблицы нет пустых клеток, то автомат называется полностью определенным. В противном случае автомат называется не полностью определенным.

2. 
   Понятие истории работы конечного автомата
   

Историей работы конечного автомата без памяти для данной входной цепочки называется упорядоченная (по моменту дискретного времени, т.е. номеру шага) совокупность троек значений {t,a,c}, где t – момент дискретного времени; a – текущий входной символ; c – текущее состояние. Для любой конечной по количеству символов входной цепочки автомат, запущенный в начальном состоянии, завершит свою работу за конечное число шагов, т. е. реализует конечную историю работы.

Историю работы автомата удобно представлять в виде таблицы, столбцы которой содержат значения троек. В качестве момента времени t _i указывается порядковый номер iтакта работы автомата.

Пусть дана входная цепочка 101 10, тогда история работы автомата будет выглядеть так (табл. 2.2.):

Таблица 2.2.

Такт	0	1	2	3	4	5	6	7	8	9	10	11	12	13
Символ	1	0	1	\d32		\d32	1		1	0	►		►
Состояние	0	2	2	2	-3	0	1	-2	0	2	2	-3	0	-1

---

Остановы автомата в состоянии -3 свидетельствуют об обнаружении двоичных чисел, в состоянии -2 – об обнаружении последовательности пробелов, в состоянии -1 – об обнаружении конца входной цепочки.

Конечный автомат, заданный вышеприведенными графом или таблицей, для любой конкретной входной цепочки при каждом запуске будут реализовывать одну и ту же историю работы.

Такие автоматы называются детерминированными.

3. 
   Детерминированность и недетерминированность
   

Однако существуют и недетерминированные автоматы, которые могут отрабатывать разные последовательности переходов из состояния в состояние при различных запусках для одной и той же входной цепочки символов. Такие автоматы играют важную роль в процессе преобразования систем регулярных определений в детерминированный конечный автомат, поэтому необходимо рассмотреть причины возникновения недетерминированности. Есть два рода (причины) недетерминированного поведения конечных автоматов.

Недетерминированностью первого рода называется наличие хотя бы одного перехода по пустой цепочке символов ε в рабочее состояние. Простой пример совокупности состояний и переходов фрагмента автомата с такой недетерминированностью, формируемый ВебТрансБидером:

0:		[other] -> 2 [–+] -> 1
1:		[other] -> 2 [0-9] -> 3
2:		[0-9] -> 3
3:		[other] -> -2 [0-9] -> 3

Этот фрагмент получен в результате выполнения первого шага преобразования [2] формального определения десятичных констант в экспоненциальной форме, содержащих показатель со знаком или без знака:

Const : [0-9]+([.][0-9]*([-+]?[eE][0-9]+)?)?

Другие формы представления этого фрагмента (он не является полностью определенным в силу того, что в управляющей таблице есть пустые клетки) показаны на рис. 2.1.:

---

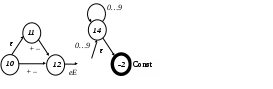
13

Рис. 2.1. Фрагменты графа состояний и УТ
Автомат, содержащий этот фрагмент, в отличие от детерминированных автоматов, при разных запусках для одной и той же входной цепочки символов может реализовывать разные истории работы. Если он находится в состоянии 10 и на входе один из символов + или –, то возможна два разных продолжения истории работы: либо переход в состояние 12 по + или –, либо переход в состояние 11 по пустой цепочке, а затем в состояние 12 по + или –.

Реализуя разные истории работы, этот автомат тем не менеекаждой входной цепочке ставит в соответствие всегда одно и то же финальное состояние.

Недетерминированностью второго рода называется наличие в управляющей таблице клеток, содержащих два или более номера состояния (или столбцов, помеченных одним и тем же символом, но не являющихся идентичными).

В графе состояний и переходов это соответствует дугам, выходящим из одной вершины, помеченным одним и тем же символом, но ведущим в разные вершины. Недетерминированность второго рода, так же, как и первого, порождает возможность реализации нескольких различных историй работы автомата для одной и той же входной цепочки при разных запусках.Пример автомата, с недетерминированностью второго рода, показан на рис. 2.2.




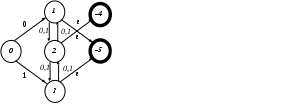
Рис. 2.2. Автомат с недетерминированностью второго рода

В управляющей таблице этого автомата есть клетки, содержащие несколько разных номеров состояний.

Недетерминированность состоит в том, что автомат, оказавшись в состоянии номер 2, может перейти по любому из символов 0 или 1 как в состояние 1, так и в состояние 3.

Несмотря на то что поведение автомата при разных запусках для одной и той же входной цепочки может быть различным, его финальное состояние для любой цепочки будет одним и тем же независимо от того, какая история работы была им реализована.

Недетерминированность автомата как первого, так и второго рода, может возникнуть в результате его построения формальными методами путем преобразования описания лексики языка.

Кроме того, недетерминированность одного рода может возникнуть в процессе эквивалентных преобразований автомата при ликвидации недетерминированности другого рода.

4. 
   Недостижимые, тупиковые и эквивалентные состояния
   

---

На рис. 2.3 показан граф состояний автомата, содержащего недостижимые, тупиковые и эквивалентные состояния. Автомат имеет два тупиковых состояния с номерами 2 и 3, три недостижимых состояния с номерами 6, 7 и 8 и эквивалентные состояния 4 и 5.




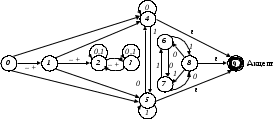
Рис. 2.3. Недостижимые, тупиковые и эквивалентные состояния

Недостижимым называется такое состояние автомата, в которое не
существует ни одного пути из начального состояния.

Тупиковым называется состояние, из которого не существует ни одного пути в какое-либо финальное состояние акцепта.

Как тупиковые, так и недостижимые состояния могут быть удалены из автомата вместе со всеми своими (как входящими, так и выходящими) дугами переходов, в результате будет получен автомат, эквивалентный исходному.

Эквивалентными называются такие два состояния, для которых строки в управляющей таблице либо полностью совпадают, либо различаются только переходами друг на друга. Любую пару эквивалентных состояний всегда можно заменить одним состоянием без потери функциональности автомата.

5. 
   Оптимальность конечных автоматов без памяти
   

Оптимальным в множестве эквивалентных друг другу автоматов называется полностью определенный детерминированный автомат, управляющая таблица которого имеет минимальное количество клеток в рабочей зоне.

Оптимальный автомат удовлетворяет следующим критериям:

1. 
   Множества символов, помечающие столбцы управляющей таблицы, попарно не пересекаются.
   
2. 
   Автомат не содержит недетерминированностей первого рода.
   
3. 
   Автомат не содержит недетерминированностей второго рода.
   
4. 
   Автомат не имеет тупиковых состояний.
   
5. 
   Автомат не имеет недостижимых состояний.
   
6. 
   Все рабочие состояния попарно не являются эквивалентными.
   
7. 
   В рабочей зоне управляющей таблице нет одинаковых столбцов.
   
8. 
   В рабочей зоне управляющей таблицы нет пустых клеток.
   

Любой конечный автомат без памяти, не удовлетворяющий хотя бы одному из этих критериев, может быть преобразован в эквивалентный ему оптимальный автомат. Методы и алгоритмы такого преобразования подробно рассматриваются в [1,2], результаты преобразования разработанной студентом системы правил должны быть изучены в этой работе.

4. 
   Порядок выполнения работы (рекомендуется использовать в качестве примера систему правил Samples/Sample2):
   

---

1. 
   Используя пакет ВебТрансБилдер, освоить:
   

• 
  создание лексических правил на языке регулярных выражений (РВ);
  
• 
  построения сложных регулярных выражений с использованием способа определения любого символа в виде «[]», квантификаторов вида {<число>,<число>} и операций выбора «|» языка РВ;
  

2. 
   Разработать (доработать разработанный при выполнении работы №1) систему правил для всех групп слов языка, определенного заданием на курсовую работу (в том числе комментариев, которые заданием не определены, но в программах на любом языке необходимы). Построить по этой системе:
   

• 
  сканер, управляемый графом состояний и переходов;
  
• 
  сканер, управляемый таблично.
  

3. 
   Изучить структуру программных модулей, построенных ВебТрансБилдером, используя операцию меню «Показать/Код транслятора», найти и изучить в этих кодах функции лексического акцепта для графового и табличного способов реализации КА, сравнить реализации конечных автоматов, управляемых различными способами. Изучить по программному коду способ реализации вызова действий, определенных в лексических правилах и алгоритм работы формирователя лексем.
   
4. 
   Проверить функционирование конечных автоматов, построенных ВебТрансБилдером:
   

• 
  подготовить тестовый пример программы на языке, заданном на курсовую работу (пример должен содержать слова абсолютно всех групп языка);
  
• 
  запустить каждый автомат на выполнение, протрассировать с использованием отладчика браузера (для открытия отладчика нажать функциональную клавишу F12) вручную работу лексического акцептора и в графовой и в табличной реализации. Для этого расставить точки останова в лексическом акцепторе и лексическом анализаторе (функции getLexem, имеющиеся и в акцепторе, и в анализаторе) и проследить процессы лексического акцепта и анализа тестовой программы (программа должна содержать несколько слов из групп «идентификаторы», «константы» и «пробелы»);
  
• 
  убедиться в работоспособности автоматов, в противном случае – доработать систему РВ и добиться правильности функционирования лексического акцептора.
  

5. 
   Построить вручную в виде двух таблиц из трех строк каждая две истории работы табличного и графового автоматов как результаты обработки ими последовательностей символов, образующих два различных оператора присваивания языка, заданного на курсовую работу.
   

---