Файл: Отчеты оформляются в виде файлов формата Microsoft Word (файлы других форматов не принимаются), размер шрифта 1214.docx

Основная задача синтаксического акцепта – проверка правильности последовательности слов транслируемой программы – формулируется так: предложение языка (т. е. последовательность терминалов порождающей язык грамматики) является правильным, если может быть установлен факт существования дерева его грамматического разбора, и неправильным в противном случае.

Само дерево разбора при этом можно и не строить, достаточно только выяснить, возможно ли это. Сложность задачи восстановления дерева разбора предложений языка (или выяснения факта его существования) существенно зависит от свойств грамматики, определяющей этот язык.

Любая грамматика G определяет единственный язык L. Однако существуют языки, для определения которых можно построить более чем одну грамматику (различающимися считаются грамматики, для которых деревья грамматического разбора хотя бы одного правильного предложения данного языка имеют разную структуру). Таков, например, язык скобочных арифметических выражений со знаками операций различного приоритета, две разные грамматики которого показаны в табл. 3.1.

Таблица 3.1

Грамматика Ga1			Грамматика G a2
1	S : S + T		1	S : U R
2	S : T		2	R : + S
3	T : T * V		3	R :
4	T : V		4	U : V W
5	V : ( S )		5	W : * U
6		V : ident	6	W :
7		V : const	7	V : ( S )
			8	V : ident
			9	V : const

Эти две грамматики различаются не только количеством правил и обозначениями нетерминалов. Пусть дано предложение

---

( a + b ) * с, где a, b и с – идентификаторы (или константы). Построим выводы этого предложения из начальных нетерминалов грамматик G_a1 и G_a2, заменяя на каждом шаге самый левый нетерминал в очередной цепочке символов на правую часть одного из правил для этого нетерминала:

Для G_a1:

S  T  T*V  V*V  (S)*V  (S+T)*V  (T+T)*V (V+T)*V 
(a+T)*V  (a+V)*V  (a+b)*V  (a+b)*c

Для G_a2:

S  UR  VWR  (S)WR  (UR)WR (VWR)WR (aWR)WR  (aR)WR  (a+S)WR  (a+UR)WR  (a+VWR)WR  (a+bWR)WR  (a+bR)WR  (a+b)WR  (a+b)*UR (a+b)*VWR  (a+b)*cWR  (a+b)*cR  (a+b)*c

Даже не преобразуя эти два вывода в графически представленные деревья грамматического разбора, легко можно заметить, что эти деревья существенно отличаются друг от друга. Таким образом, действительно существуют эквивалентные, но различающиеся по своим свойствам грамматики, определяющие один и тот же язык.

Свойства грамматик оказывают большое влияние как на принципиальную возможность использования данной грамматики для синтаксического анализа, так и на применимость средств автоматизации построения синтаксических анализаторов.

Все грамматики можно разделить на четыре основных класса по Хомскому, впервые сформулировавшему приведенные ниже признаки деления на иерархически вложенную систему классов: общие, контекстно-зависимые, контекстно-свободные и регулярные.

Для целей построения синтаксических анализаторов трансляторов наилучшим образом подходят контекстно-свободные грамматики, у которых левая часть каждого правила представляет собой в точности один нетерминал, а на правые части не накладывается никаких ограничений. Они позволяют определять синтаксис формальных языков, в том числе языков программирования, т.е. совокупность правил построения предложений языка из его слов.

Независимость от контекста означает возможность подстановки правой части любого из правил для замены нетерминала из левой части правила в любой цепочке, содержащей этот нетерминал.

3. 
   Свойства контекстно-свободных грамматик
   

Свойства любой грамматики полностью определяются ее системой порождающих правил и могут служить основанием для разбиения всего класса контекстно-свободных грамматик на более узкие подклассы. Для некоторых подклассов контекстно-свободных грамматик известны эффективные алгоритмы автоматизации проектирования трансляторов для порождаемых или языков.

---

Наиболее важными свойствами грамматик в целом являются рекурсивность и однозначность.

Рекурсивность

Нетерминальный символ X называется рекурсивным, если из него могут быть выведены цепочки, содержащие сам этот символ X, т. е.

X  μ X η,

Существует много вариантов свойства рекурсивности нетерминалов: прямая и косвенная, левая, правая и общая. Эти варианты могут сочетаться произвольным образом. Грамматика называется рекурсивной, если рекурсивен хотя бы один нетерминальный символ, и нерекурсивной в противном случае.

Нерекурсивные грамматики с конечным количеством порождающих правил определяют так называемые конечные языки, в которых количество правильных предложений ограничено. Такие языки и грамматики не представляют практического интереса.

Однозначность

Грамматика называется однозначной, если любое правильное предложение порождаемого ею языка имеет единственное дерево грамматического разбора, и неоднозначной в противном случае. Грамматики G_a1и G_a2 являются однозначными, но для того же самого языка можно привести пример неоднозначной грамматики, показанный в табл. 3.2.

Выявление свойства однозначности некоторой грамматики является алгоритмически неразрешимой проблемой. Не существует универсального алгоритма, способного для любой заданной контекстно-свободной грамматики определить, однозначна ли она. Известно, что методы построения синтаксических анализаторов путем преобразования формальной грамматики в конечный автомат не приводят к желаемому результату для неоднозначных грамматик. Другими словами, неоднозначные грамматики непригодны для преобразования в конечный автомат (со стековой памятью), выполняющий функции синтаксического анализатора. Однако и многие однозначные грамматики также не допускают подобного преобразования, но по другим причинам.

Таблица 3.2

Грамматика Ga3
1	S : S + S
2	S : T
3	T : T * T
4	T : V
5	V : ( S )
6	V : ident
7	V : const

---

Кроме общих свойств грамматик важное значение для решения задач синтаксического анализа имеют некоторые свойства нетерминальных символов и отношения между символами грамматики.

Свойства символов грамматики

Аннулируемость

Нетерминальный символ называется аннулируемым, если из него может быть выведена пустая цепочка символов. В противном случае нетерминал называется неаннулируемым. В литературе по формальным языкам такие символы обычно называются аннулирующими и неаннулирующими.

Это свойство нетерминальных символов может иметь важное значение для свойств грамматики в целом и ее применимости в том или ином методе синтаксического анализа.

Недостижимость

Символ (терминальный или нетерминальный) называется недостижимым, если он не появляется ни в одной цепочке символов, выводимой из начального нетерминала грамматики.

Бесплодность

Нетерминальный символ называется бесплодным, если из него не может быть выведена цепочка, состоящая только из терминалов.

Недостижимые и бесплодные нетерминалы могут появиться в грамматике либо в результате ошибок при разработке ее системы порождающих правил, либо в результате эквивалентных преобразований грамматики с целью изменения ее свойств или свойств ее символов. Все правила, содержащие такие символы, следует удалить из грамматики (а сами символы из ее алфавитов). Алгоритмы вычисления свойств символов грамматики следует изучить по [1].

Кроме свойств отдельных символов большое значение для целей синтаксического анализа имеют некоторые отношения между символами, определяемые всей совокупностью правил грамматики.

Важнейшими отношениями являются отношение предшествования и отношение следования. Эти отношения вычисляются в виде множеств, сопоставляемых с символами грамматики и содержащих опять-таки символы этой грамматики.

4. 
   Множества предшественников символов грамматики
   

Предшественником некоторого символа X называется символ, с которого начинается цепочка, выводимая из X. Считается, что любой символ является предшественником самого себя (т. е. допускается вывод длины 0).

Термин «предшественник» в русском языке имеет несколько другой смысл: нечто, появляющееся до того, чему оно предшествует. Тем не менее в литературе по формальным языкам и грамматикам (и в настоящем учебнике) этот термин используется именно в том смысле, который определен в предыдущем абзаце.

---

5. 
   Множества предшественников цепочек символов
   

При построении синтаксических анализаторов часто приходится оперировать не с отдельными символами, а с цепочками символов.

В множество предшественников цепочки  входят те и только те терминальные символы, с которых начинаются цепочки, выводимые из .

Если известны множества предшественников одиночных символов грамматики, то можно легко сформулировать способ определения множеств предшественников произвольных цепочек символов.

Пусть цепочка имеет вид  = ABCD..., где A, B, C, D, ... – произвольные (не обязательно нетерминальные) символы грамматики. Пусть также известны множества предшественников всех символов грамматики.

Тогда множество предшественников цепочки  можно вычислить по следующей формуле:



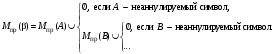
Здесь 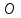– пустое множество, под неаннулируемым символом понимается либо терминал, либо неаннулируемый нетерминал.

6. 
   Множества последователей символов грамматики
   

Символ Y называется последователем символа X, если хотя бы в одной цепочке ω, выводимой из начального нетерминала грамматики, символ Y непосредственно следует за X:

S  ω = ... X Y ...

Это определение понятия последования не является конструктивным. Для того чтобы можно было понять, что такое последователи и построить процедуру определения множеств последователей для символов грамматики, нужно точно сформулировать условия возникновения отношения последования.

Символ Y является непосредственнымпоследователем символа X, если выполняется либо условие 1, либо условие 2:

Условие 1. В грамматике есть правило вида

N :  XY , где  и  – произвольные, возможно пустые цепочки.

Условие 2. В грамматике есть правило вида

N :  X  Y , где  и  – произвольные, возможно пустые цепочки, а  – цепочка, состоящая только из аннулируемых нетерминалов.

Непосредственными последователями, к сожалению, полные множества последователей символов грамматики не исчерпываются.

Символ Y является последователем символа X, если Y является последователем (неважно – непосредственным или нет) некоторого символа Z

---