Файл: Учебнометодический комплекс Для студентовбакалавров, обучающихся по направлению.doc

₄=1.

Тогда



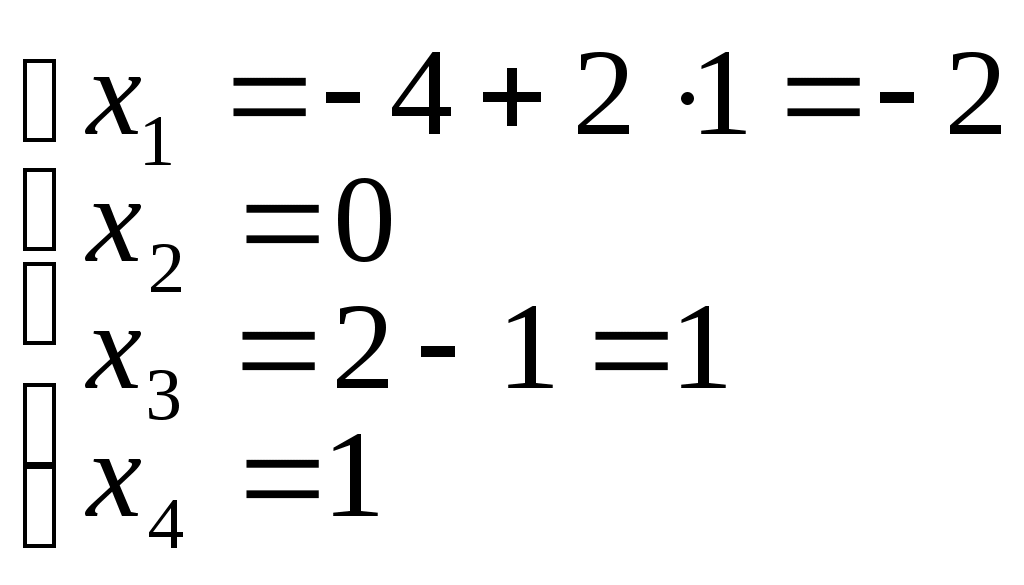
Так как свободным переменным мы можем давать любые числовые значения, то будем получать бесконечное множество решений системы.

Замечание 1. Теорему (1) можно сформулировать в терминах ранга матриц. Действительно, пусть rang А=r₁ , rangВ= r₂, где А -матрица системы (1), В - расширенная матрица системы (1)

B =

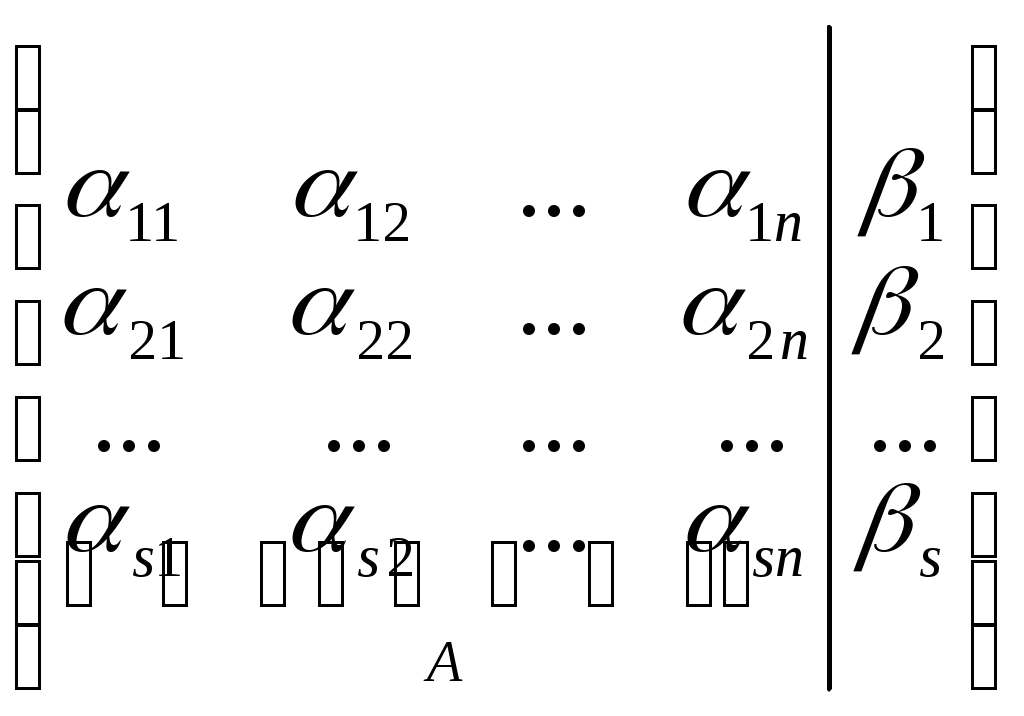
Теорема 1. (Теорема Кронекера-Капелли).

Система: где i=1, 2, ..., k будет:

1) совместной, если rang A = rang В;

2) совместной и неопределённой, если rang A = rang B < n;

3) несовместной, если rang А  rang В.

Пример 2. Выяснить, совместна ли система



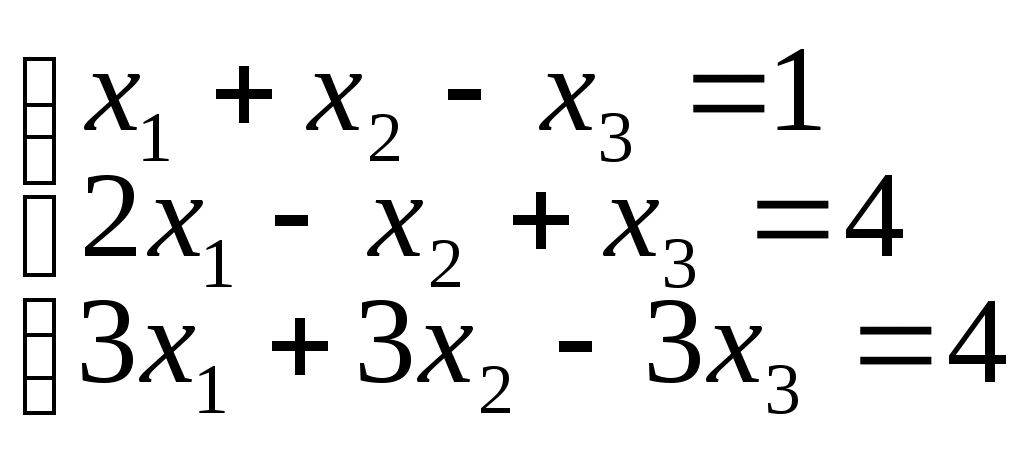
Решение.

Составляем расширенную матрицу В и одновременно находим ранги матриц А и В.

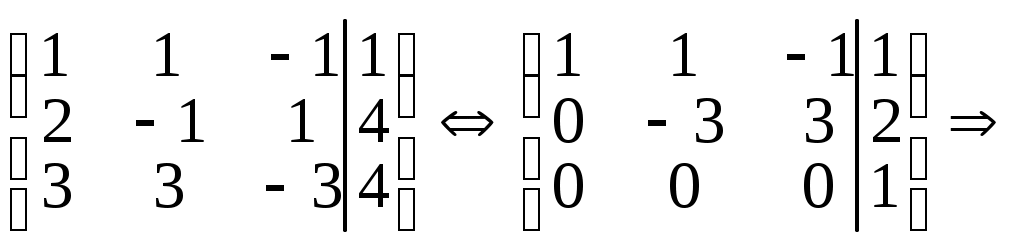RangA=2, RangB=3 Значит, система не имеет решений

Понятие обратимой матрицы лежит в основе матричного метода решения систем линейных уравнений.

В отличие от универсального (общего) метода Гаусса, этот метод имеет существенные ограничения, так как его можно применять лишь для решения систем вида:

1)

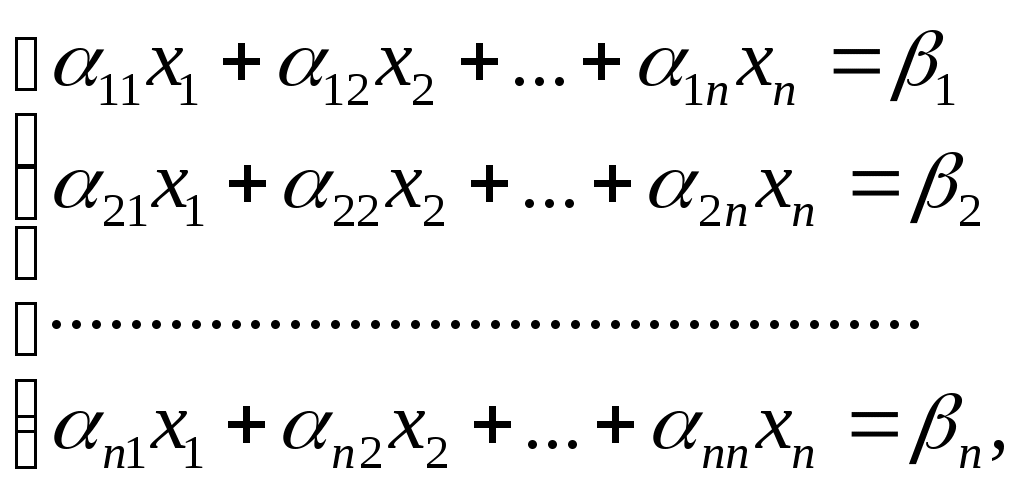
матрица А = ||_ik||которых должна быть обратима. Тогда систему (1) можно записать в виде матричного уравнения (2) АХ=В, где

А = 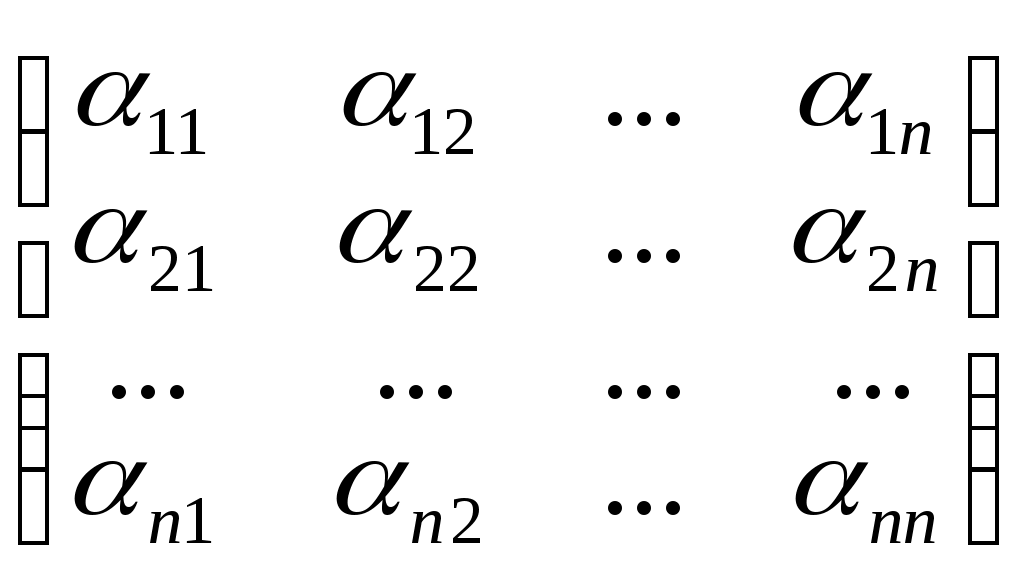Х = В =

Так как А - обратима, то найдя матрицу А^-1, из уравнения (2) можно выразить матрицу Х= А^-1 В.

Замечание. Здесь важно соблюдать порядок умножения матриц (слева или справа), так как умножение матриц некоммутативно.

Пример 3. Решить систему матричным методом

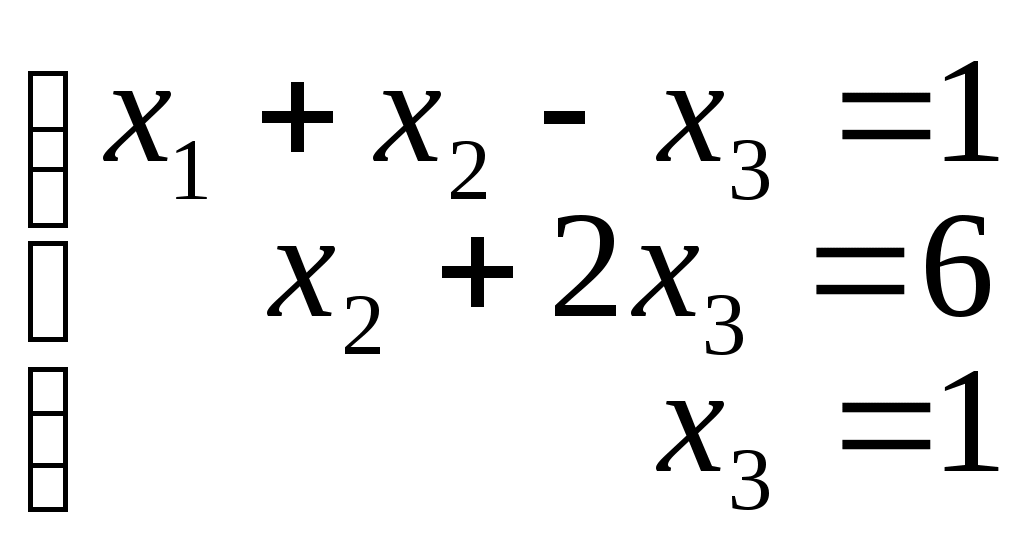
Введём обозначения:

А =

---

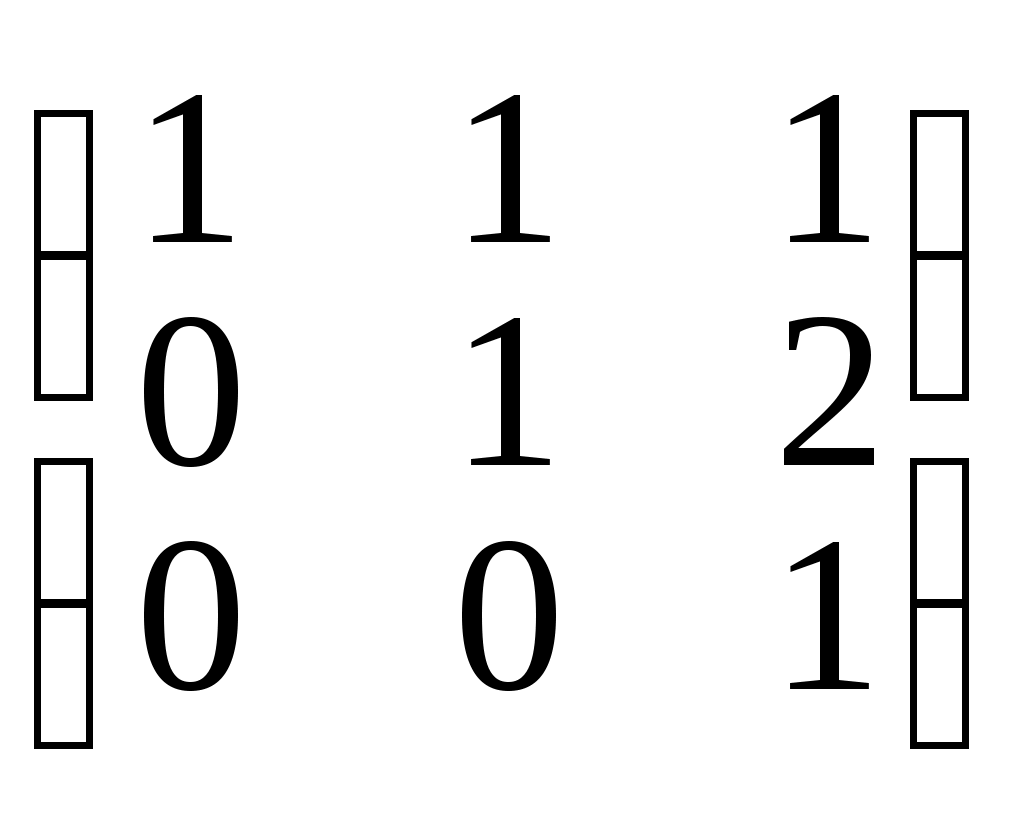
, Х = , В =

Тогда система в матричной форме будет иметь вид: (*)АХ=В

Так как rangА=3 и ее порядок 3x3, тo  А^-1: А^-1 А=А А^-1 = Е. Если равенство (*) домножить слева на А^-1, то получим:

А^-1АХ = А^-1В => Х= А^-1 В

Чтобы теперь найти X, нужно вычислить А^-1 и найти произведение А^-1В.

(A|E)=



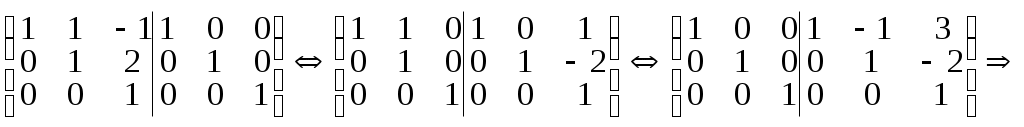
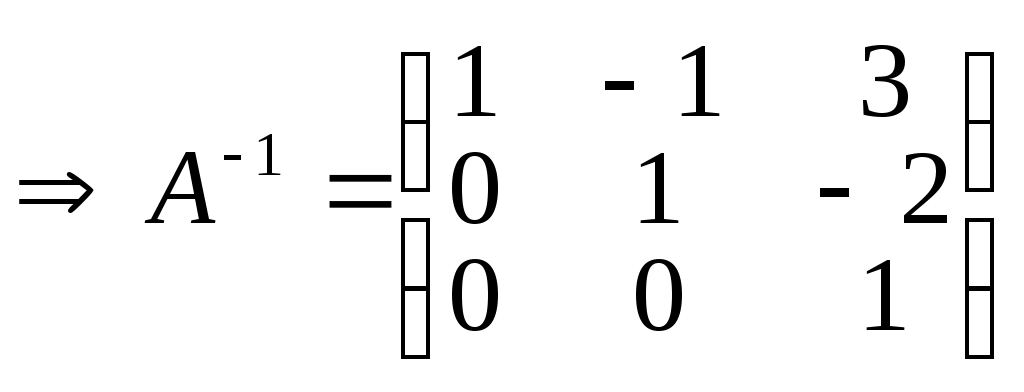
X = 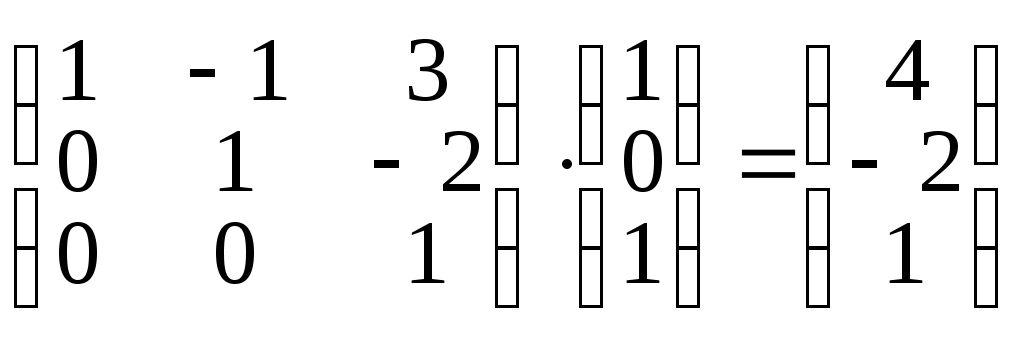x₁ = 4, x₂ = -2, x₃= 1

Проверка:



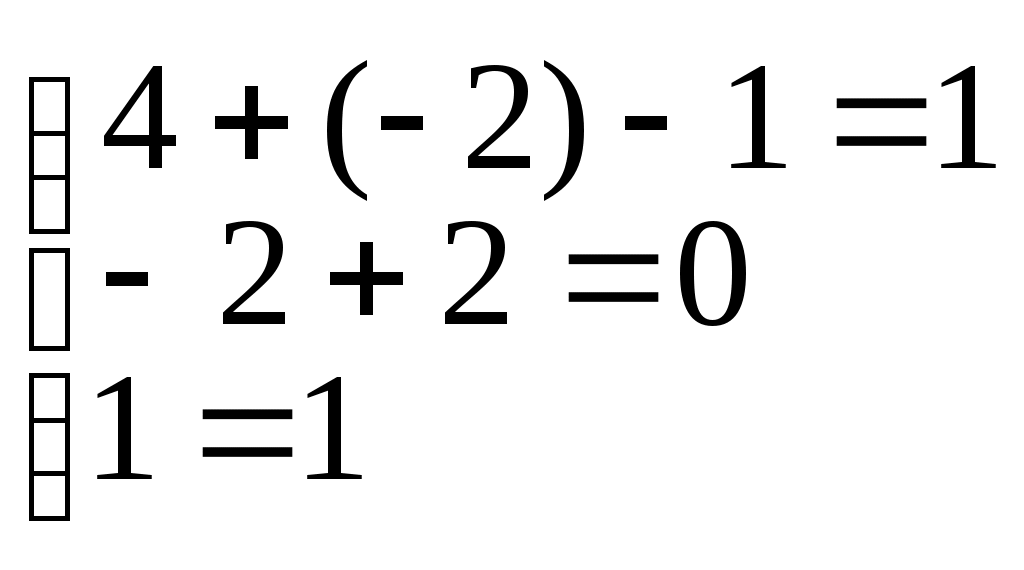
Понятие определителя n-гопорядка позволило разработать ещё один локальный метод решения систем линейных уравнений. Если дана система (n) уравнений с nпеременными

где i=1, 2, ...,n

и определитель матрицы этой системы отличен от нуля, то есть

|A| 0, то решение этой системы можно вычислить по формулам Крамера: i = 1, 2,…, n, где |A| - определитель матрицы А данной системы, а определители |A_i| получаются из определителя |A|путём последовательной замены i-го столбца столбцом свободных членов.

Пример 4. Решить систему методом Крамера:



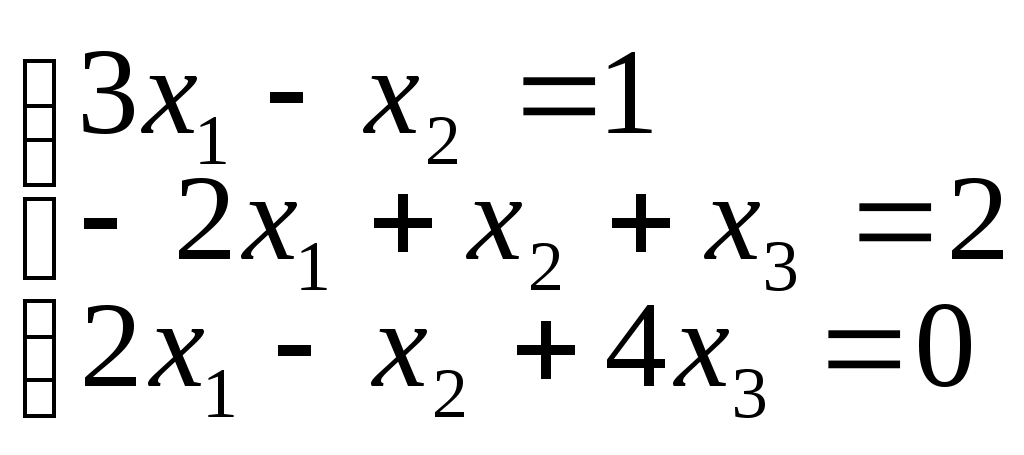
Вычисляем определитель матрицы А этой системы

|A| = 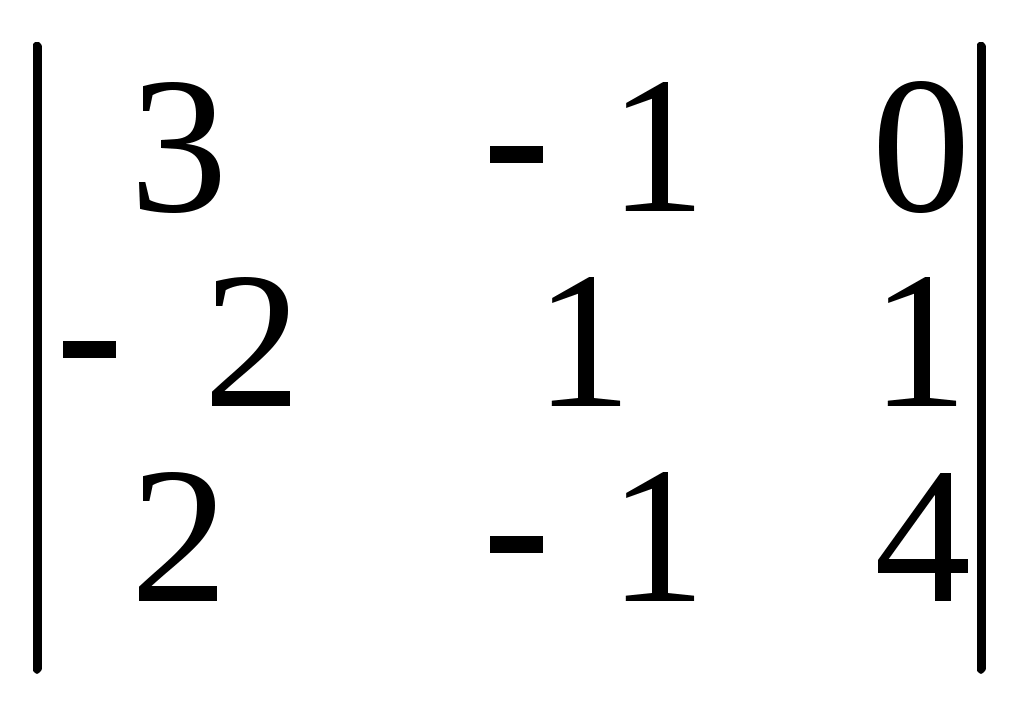= 12-2+0-0-8+3=5

Заменив в этом определителе первый столбец столбцом свободных членов, получим определитель |A₁|

|A₁| = 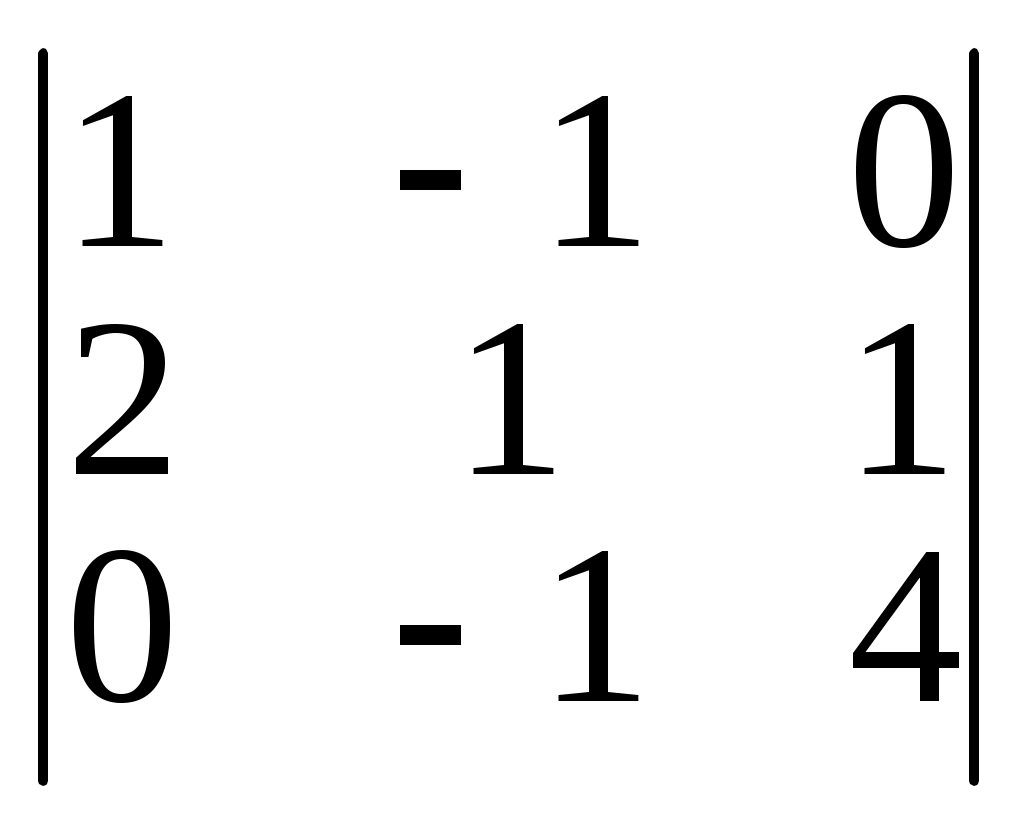= 4+0+0+8+1+0=13

Заменив в определителе |A| второй столбец столбцом свободных членов, получим определитель

|A₂| = 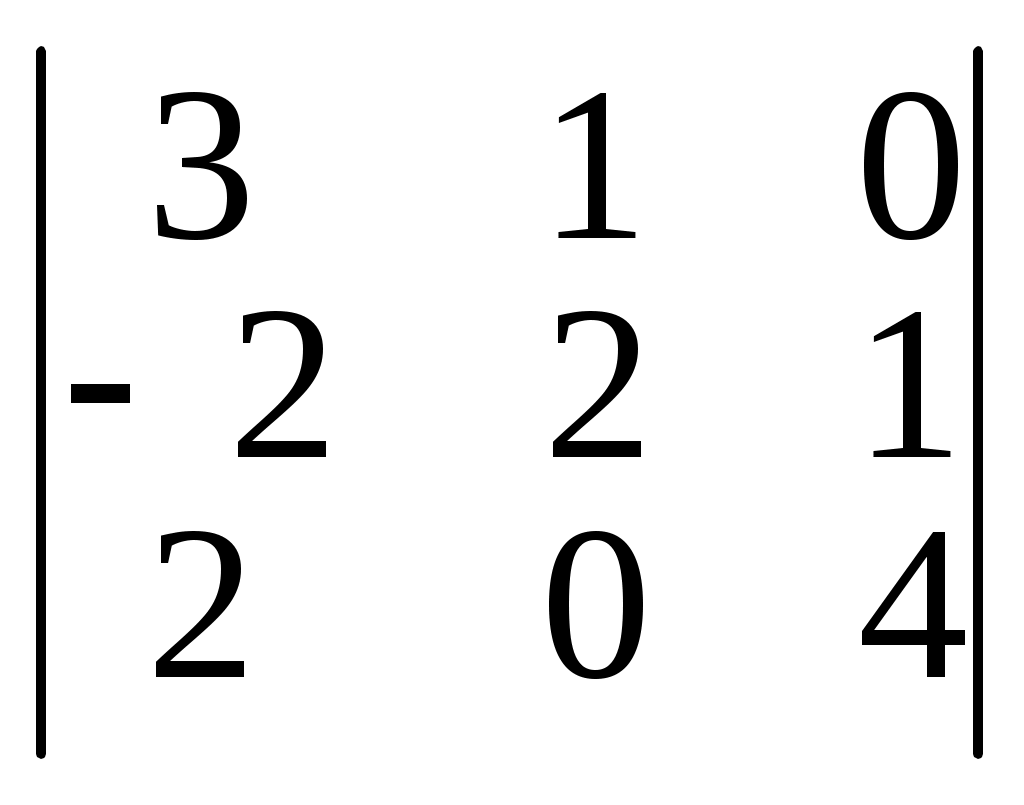= 34

Аналогично находим и вычисляем определитель•

|A₃| =

---

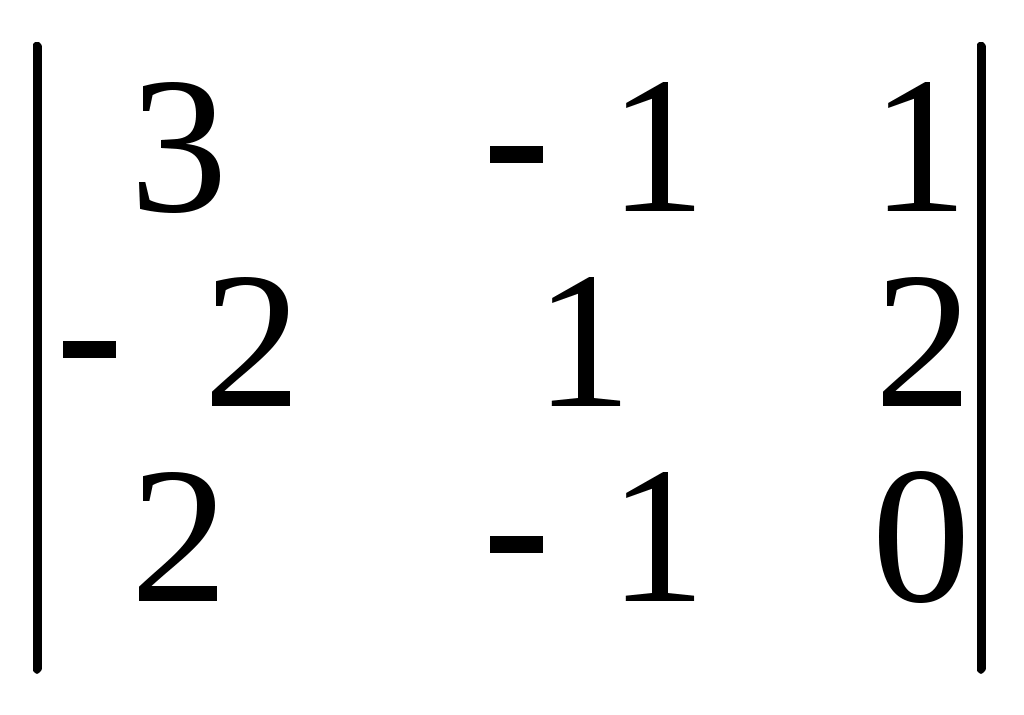= 2

Тогда x₁ = ; x₂ = ; x₃ =


Проверка:
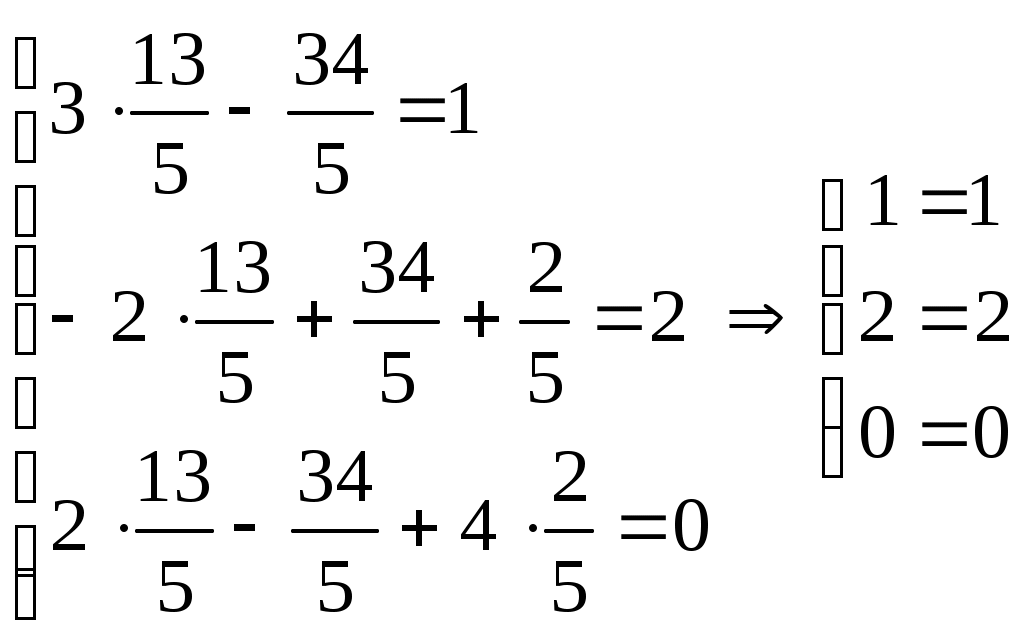
С системой (1) где i=1, 2, ..., kвсегда можно связать систему (2) , которая называется системой линейных однородных уравнений. Эта система всегда совместна, так как вектор  = (0, 0,..., 0) является её решением, кроме этого, для этой системы всегда rang A=rangВ, т.к. столбец свободных членов равен нулю. Поэтому, если rang A
Теорема 2. М,+ {|  R.} - является линейным пространством.

Доказательство:

В данном случае не нужно проверять все аксиомы линейного пространства, т.к. решением системы (элементами множества М) являются арифметические векторы, то достаточно доказать, что М является подпространством Rⁿ .

Для этого нужно взять любые два решения системы (2) и показать, что их сумма будет решением системы (2), а так же произведение любого решения на действительное число снова будет решением системы (2). Действительно: пусть b = (₁, ₂, …, _n,) и c = (₁, ₂, …, _n,) - решения системы (2). Найдём b + c = (₁+ d₁, b₂+ d₂,…, b_n+d_n) и подставим в систему (2), получим: _i1(₁+ d₁) + _i2(₂+ d₂) + …+ _in(_n+ d_n) = (_i1₁ + _i2₂ +…+ _in_n) + +(a_i1d₁ + a_i2d₂ +…+ a_ind_n )=0+0=0

Аналогично, b=(₁, ₂, …, _n), a_i1(b₁)+a_i2(b₂)+…+a_in(b_n) = (_i1₁+_i2₂ +…+_in_n) = •0 = 0

Итак, М,+ {|  R.} - линейное пространство.

Базу этого пространства называют фундаментальной системой решений (Ф.С.Р.).

Покажем на конкретном примере алгоритм её нахождения.

Пример 5. Найти Ф.С.Р. для системы:



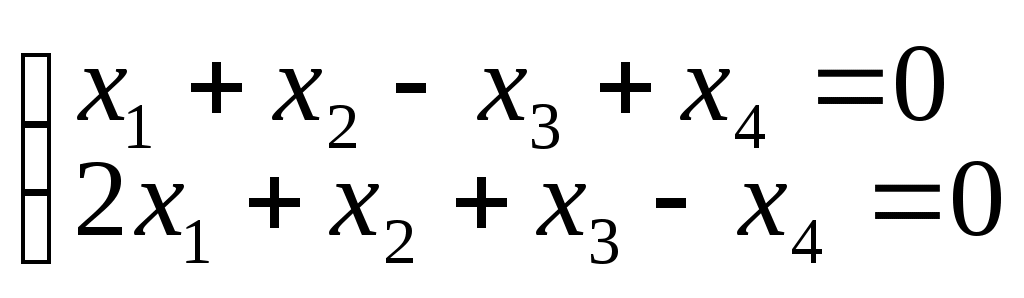
Решение.

1 шаг. Методом Гаусса находим общее решение данной системы:

---

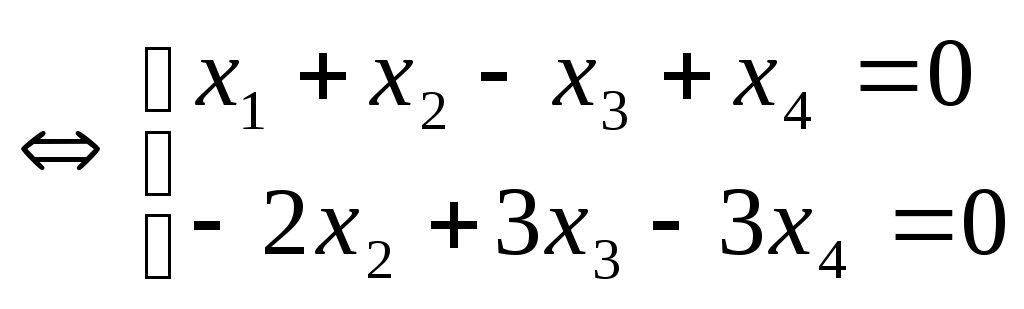
Пусть X₃, X₄ – свободные переменные, X₁, X₂ – главные.

Тогда 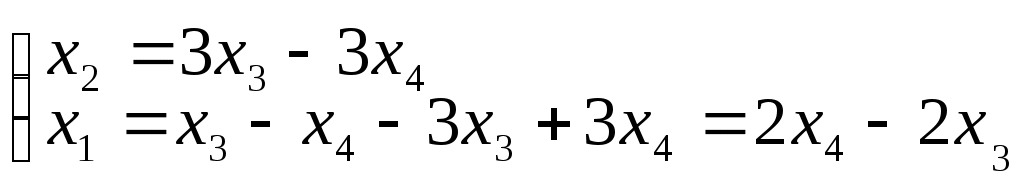- общее решение системы .

2 шаг. Записываем таблицу:

X1	X2	X3	X4
-2	3	1	0
2	-3	0	1

свободным переменным придаём значения (1,0) и (0,1) и вычисляем главные переменные.

Тогда два вектора C₁ = (-2,3,1,0), С₂=(2,-3, 0, 1) будут базой пространства М (Ф.С.Р.).

---

Глава 4. Комплексные числа.

Содержание темы.

Теорема о существовании поля комплексных чисел. Действия над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексных чисел, тригонометрическая форма записи, действия над комплексными числами в тригонометрической форме.

Основные умения и навыки, которыми должны овладеть студенты в процессе изучения этой темы:

- уметь изображать комплексные числа на координатной плоскости в виде точек и радиус-векторов и наоборот;

- уметь находить модуль и аргумент zC, переходить от алгебраической формы записи комплексного числа к тригонометрической и наоборот;

- уметь выполнять арифметические операции над комплексными числами в алгебраической и тригонометрической форме, понимать их геометрический смысл;

- использовать полученные знания при решении задач алгебры и геометрии.

Все теоретические положения и практические выводы этой темы вытекают из теоремы о существовании поля комплексных чисел.

Теорема 1: Существует единственное, с точностью до изоморфизма, поле С, в котором выполняются следующие условия:

1. Поле R является подполем поля С.

2. i² = -1

3. zC х, yR: z = x+ iy

Запись комплексного числа zв виде х + iy называется его алгебраической формой, при этом (х) называют действительной частью комплексного числа, iy - мнимой частью, а (у) – коэффи-циентом мнимой части. Обозначение: Re z - действительная часть, Im z - мнимая часть комплексного числа.

Так как (z = х + iy)  (C = R x R), то с геометрической точки зрения, любое комплексное число имеет две равноправные геометрические интерпретации (модели).

а) точка координатной плоскости А (х, у);

б) радиус-вектор с концом в точке с координатами (х, у)

Геометрический подход к понятию комплексного числа позволяет записывать его в так называемой тригонометрической форме.

Для этого вводятся понятия модуля и аргумента комплексного числа.

Определение 1: Модулем комплексного числа z называется арифметическое значение корня квадратного из х

---