Файл: Лабораторная работа 1. Операционная система Windows. Основные принципы работы. Цель работы.doc

Для построения поверхности выполнить следующие действия:

• 
  Выделить таблицу данных, включая заголовки.
  
• 
  Нажать пиктограмму Мастер диаграмм.
  
• 
  Выбрать тип диаграммы Поверхность (подтип 1).
  
• 
  Закончить построение диаграммы.
  

2. Установка высоты и перспективы объемной диаграммы. В зависимости от типа диаграммы и выбранных параметров можно изменить высоту и перспективу объемной диаграммы и установить или отменить перпендикулярные оси.

• 
  Выполнить щелчок правой кнопкой мыши на области диаграммы и выбрать в контекстном меню команду Объемный вид.
  
• 
  Установить необходимые параметры. (Внимание! Параметр Перспектива недоступен на объемных диаграммах, в которых установлен флажок Перпендикулярные оси).
  

3. Форматирование делений диаграммы. Тип делений можно определить в соответствии с желанием пользователя.

• 
  Установить указатель мыши на форматируемую ось и дважды нажатье кнопку мыши. В наборе переключателей Шкала установить следующие параметры: минимальное значение 8, цена основных делений 2.
  
• 
  Посмотреть, как изменится диаграмма, если установить цену основных делений 0,5.
  

4. Построить график функции z=x²/4+y², x меняется от -10 до 10 с шагом 1, y меняется от -1 до 1 с шагом 0,1.

При построении трехмерных графиков используют Таблицу подстановки. Для заполнения таблицы подстановки нужно:

• 
  Перейти на новый лист.
  
• 
  Ввести в ячейку А1 «x=», в ячейку А2 – «y=». Ячейка В1 в дальнейшем будет ячейкой ввода для переменной x, а ячейка В2 - для переменной y. (Ячейка ввода - это ячейка, в которую последовательно подставляются значения для заполнения таблицы данных).
  
• 
  В третьей строке заполнить значения переменной x, начиная с ячейки В3 ( в ячейку В3 занести значение -10, в С3 -9 и т.д. до 10).
  
• 
  Записать значения переменной y в столбец А, начиная с ячейки А4 (ввести в ячейку А4 значение -1, в А5 -0,9 и т.д. до 1).
  
• 
  В ячейку А3 ввести формулу = B1^2/4+B2^2.
  
• 
  Выделить диапазон таблицы, содержащий формулу и подставляемые значения.
  
• 
  В меню Данные выбрать команду Таблица подстановки.
  
• 
  В поле Подставлять значения по столбцам в ввести ссылку на ячейку ввода В1, в которую затем будут автоматически последовательно подставляться значения ячеек, расположенных в строке правее формулы. (Переменная x изменяется по столбцам!).
  
• 
  В поле Подставлять значения по строкам в ввести ссылку на ячейку ввода В2, в которую будут последовательно подставляться значения ячеек, расположенных в столбце ниже формулы. (Переменная y изменяется по строкам!).
  
• 
  По полученной таблице построить поверхность. Обозначить оси и задать заголовок.
  

---

5. 
   Сохранить рабочую книгу на диске.
   

---

Лабораторная работа №16. Расчеты в Excel

Цель работы: освоение некоторых математических функций, процедур Подбор параметра и Поиск решения.
Элементы линейной алгебры

1. Вычислить определитель квадратной матрицы 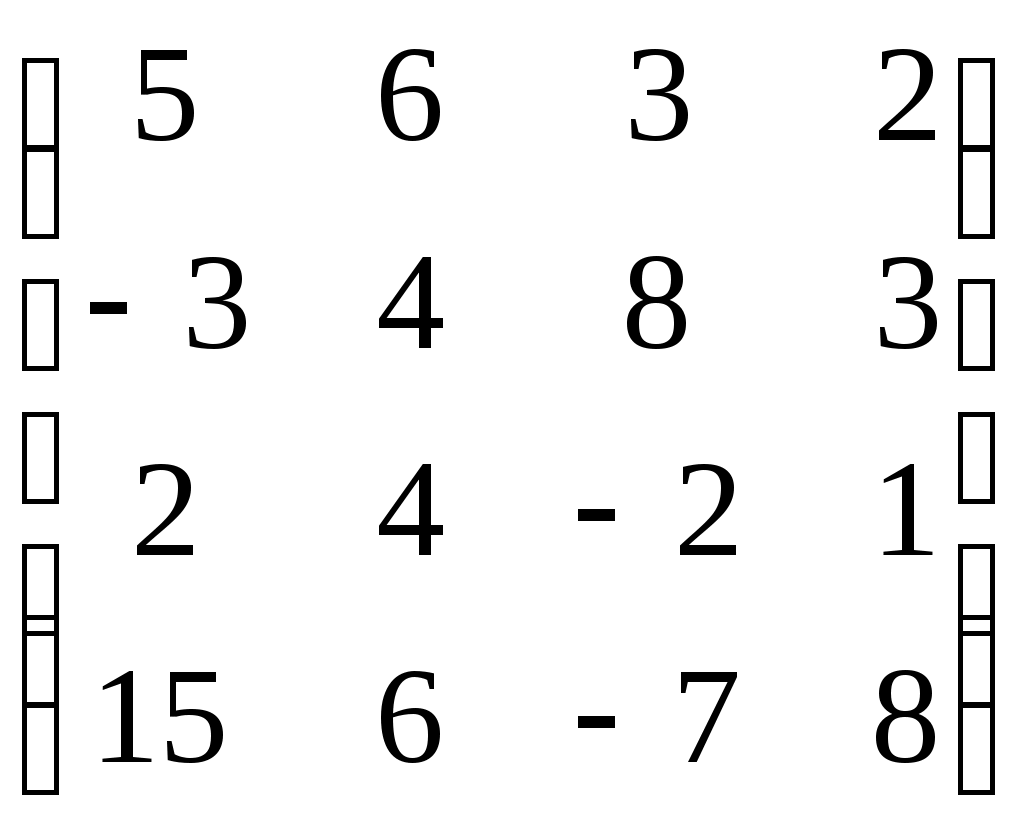, используя математическую функцию МОПРЕД. Для этого:

• 
  Ввести исходную матрицу (каждый элемент матрицы занести в свою ячейку).
  
• 
  Установить указатель мыши в свободную ячейку (для результата) и вызвать нужную функцию с помощью Мастера функций.
  
• 
  В диалоговом окне ввести диапазон значений исходной матрицы.
  

2. Вычислить обратную матрицу квадратной матрицы, используя математическую функцию МОБР.

Для этого:

• 
  Занести в таблицу исходную матрицу.
  
• 
  В свободном месте таблицы выделить блок для обратной матрицы (размерность обратной матрицы совпадает с размерностью исходной матрицы).
  
• 
  Вызвать Мастер функций, выбрать в классе математических и тригонометрических функций требуемую функцию.
  
• 
  В диалоговом окне функции указать диапазон, в котором находится исходная матрица, нажать «OK». В выделенном под обратную матрицу блоке появится первый элемент вычисленной обратной матрицы.
  
• 
  Поставить курсор в строку формул, выполнить комбинацию клавиш «Ctrl»+«Shift»+«Enter». В выделенном блоке появится вычисленная обратная матрица.
  

3. Вычислить произведение матриц 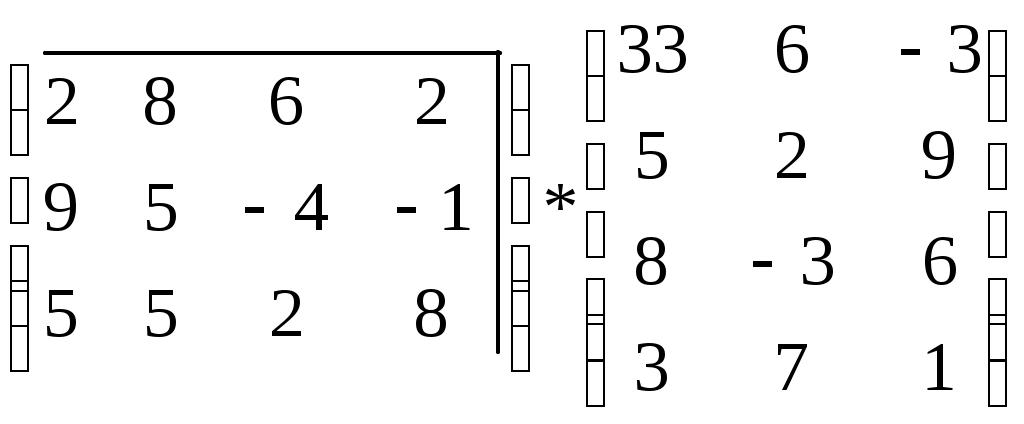, используя математическую функцию МУМНОЖ. Для этого выполнить действия аналогично предыдущему пункту.

4. Решить систему линейных уравнений



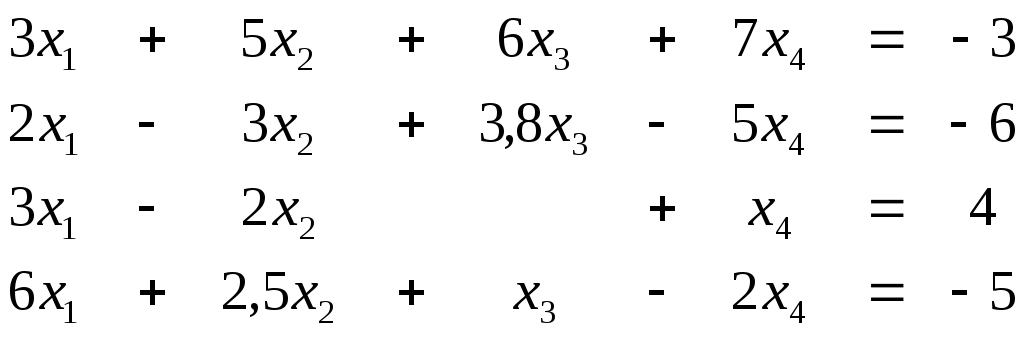
методом обратной матрицы.

Метод обратной матрицы заключается в следующем: пусть дана система линейных уравнений вида A*X=B, где A - матрица коэффициентов при неизвестных; X - вектор неизвестных; B - вектор свободных членов.

Тогда

---

, где - обратная матрица матрицы A.

Для решения необходимо выполнить следующее:

• 
  Занести в таблицу исходную матрицу коэффициентов при неизвестных.
  
• 
  Занести в таблицу столбец свободных членов.
  
• 
  Вычислить обратную матрицу матрицы коэффициентов при неизвестных.
  
• 
  Выделить диапазон ячеек для столбца неизвестных.
  
• 
  Умножить обратную матрицу на столбец свободных членов.
  

Сделать проверку (умножить исходную матрицу коэффициентов при неизвестных на полученный столбец значений неизвестных).

Работа с процедурой Подбор параметра

Подбор параметра - средство Excel для анализа таблицы, при котором значения ячейки-параметра изменяются так, чтобы число в целевой ячейке стало равным заданному. С помощью этого средства возможен, например, поиск решения уравнения с одним неизвестным. Решение задачи производится через команду Подбор параметра меню Сервис. В диалоговом окне устанавливается адрес целевой ячейки, ее значение, адрес ячейки параметра.

Программа Подбор параметра доступна только в том случае, если она отмечена в диалоговом окне Надстройки, которое открывается с помощью команды Надстройки меню Сервис.

1. Решить уравнение , используя Подбор параметра. Для этого:

• 
  В ячейку А1 ввести текст «х=».
  
• 
  Ввести начальное значение переменной x в ячейку B1. Т.к. х – неизвестное, то начальное значение можно взять любое (например, ноль).
  
• 
  В ячейку А3 ввести текст «Левая часть уравнения».
  
• 
  В ячейку А4 ввести формулу =5*А1^2-2*A1+6.
  
• 
  В ячейку D3 ввести текст «правая часть уравнения».
  
• 
  В ячейку D4 ввести число 8.
  
• 
  В ячейку C4 ввести текст «=».
  
• 
  Выполнить команду Подбор параметра. Установить:
  
• 
  адрес целевой ячейки – А4; значение целевой ячейки - 8; изменяя ячейку - B1. Таким образом, процедура Подбор параметра будет автоматически изменять значение в ячейке B1, то есть x, до тех пор, пока значение целевой функции в ячейке A4 не станет равным 8.
  

2. Решить уравнения, используя процедуру

---

Подбор параметра:

а) ;

б) ;

в)

3. 
   Решить задачу: известен размер вклада, который будет помещен в банк на некоторый срок под определенный процент. Требуется рассчитать сумму возврата вклада в конце периода и определить условия помещения вклада, наиболее подходящие для его владельца.
   

• 
  Создать таблицу:
  

Таблица 10. – Вклады

Размер вклада, руб.	5000
Срок вклада, лет	5
Процентная ставка	5%
Коэффициент увеличения вклада
Сумма возврата вклада, руб.

Коэффициент увеличения вклада при начислении сложных процентов вычисляется по формуле: =(1+процентная ставка)^(срок возврата вклада).

Сумма возврата вклада вычисляется по формуле:

=(размер вклада)*(коэффициент увеличения вклада)

• 
  Скопировать таблицу. В копии, используя Подбор параметра, рассчитайте процентную ставку, при которой сумма возврата вклада будет составлять 8000 рублей.
  
• 
  Скопировать исходную таблицу. В копии, используя Подбор параметра, рассчитайте срок вклада, при котором сумма возврата вклада будет составлять 8000 рублей.
  

Работа с процедурой Поиск решения

Программа Поиск решения представляет собой мощный вспомогательный инструмент для выполнения сложных вычислений. Она позволяет по заданному значению результата находить множество значений переменных, удовлетворяющих некоторым указанным критериям.

Исходные данные для программы Поиск решения должны быть представлены в виде таблицы, которая содержит формулы, отражающие зависимости между данными в таблице.

Запуск программы Поиск решения осуществляется с помощью команды Поиск решения меню Сервис. Эта программа доступна в том случае, если в диалоговом окне Надстройки помечена категория

---