ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 94
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ZN =
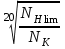 при NK >
при NK > 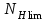 , (2.8)
, (2.8)но не менее 0,75,
где NHlim – базовое число циклов перемены напряжений;
NК – суммарное число циклов перемены напряжений.
Суммарное число циклов перемены напряжений NК при постоянной нагрузке определяется следующим образом (и для шестерни, и для колеса):
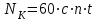 , (2.9)
, (2.9)где с – число зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом (в данном задании с = 1);
n – частота вращения рассчитываемого зубчатого колеса, об/мин;
t – срок службы передачи, в часах.
Если не задано конкретное число часов работы передачи, а задан срок работы передачи в годах, то t определятся по формуле
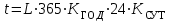 , (2.10)
, (2.10)где L – срок службы в годах;
КГОД, КСУТ– коэффициенты использования передачи в течение года и суток соответственно.
Базовое число циклов перемены напряжений
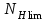 определяется по графику, представленному на рис. 2.6.
определяется по графику, представленному на рис. 2.6. 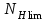 , млн циклов , млн циклов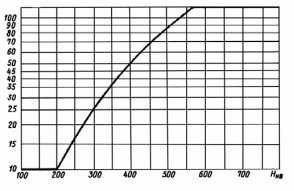 |
| Рис. 2.6. График для определения базового числа циклов перемены напряжений 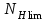 |
Используя все найденные параметры, определяют межосевое расстояние. Полученное межосевое расстояние при необходимости округляется до стандартного значения:
-
РЯД 1 – 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400; -
РЯД 2 – 71, 90, 112, 140, 180, 225, 280, 355, 450.
Значения первого ряда следует предпочитать значениям второго.
2.2. Проектирование передачи
1. Ориентировочно значение модуля при проектировочном расчете зубчатых передач можно принять, мм:
– при твердости Н350НВ m= (0,01...0,02)aw; (2.11)
– при твердости H45HRCэ т = (0,016...0,0315)aw. (2.12)
По ГОСТ 9563–80 принимают стандартный нормальный модуль:
-
РЯД 1 – 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; -
РЯД 2 – 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14.
Значения первого ряда следует предпочитать значениям второго.
2. Определяется суммарное число зубьев и число зубьев шестерни и колеса:
– предварительно принимают угол наклона зубьев
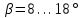 и определяют суммарное zC число зубьев шестерни z1 и колеса z2:
и определяют суммарное zC число зубьев шестерни z1 и колеса z2: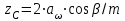 ; (2.13)
; (2.13)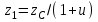 ; (2.14)
; (2.14)– полученные значения чисел зубьев округляем до целого числа:
z2 = zС –z1. (2.15)
3. Определяются действительное передаточное число и его погрешность:
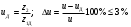 . (2.16)
. (2.16)Погрешность передаточного числа не должна превышать 3 %.
4. Уточняем значение угла β:
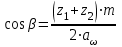 , (2.17)
, (2.17)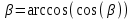 . (2.18)
. (2.18)Значение угла наклона зубьев необходимо вычислять с точностью до секунд.
5. Далее определяются основные размеры шестерни и колеса.
Делительные диаметры шестерни и колеса:
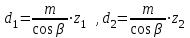 . (2.19)
. (2.19)6. Проверку полученных диаметров можно провести с помощью формулы
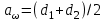 . (2.20)
. (2.20)Проверкой должно быть установлено, что межосевое расстояние сходится со значением, принятым ранее.
7. Диаметры вершин зубьев определяются по формулам:
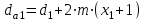 ,
, 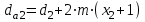 . (2.21)
. (2.21)Диаметры впадин:
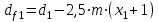 ,
, 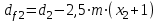 , (2.22)
, (2.22)где
x – коэффициент смещения, мм.
8. Ширина колеса определяется по формуле, мм:
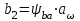 . (2.23)
. (2.23)Полученное значение ширины колеса округляем до нормального линейного размера.
9. Ширина шестерни определяется по формуле, мм:
b1 = b2 + (5...10). (2.24)
Полученное значение ширины округляем до нормального линейного размера.
10. Определим окружную скорость зубчатых колес по формуле, м/с:
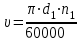 . (2.25)
. (2.25)11. По окружной скорости колес с учетом рекомендации табл. 2.6 назначают степень точности зубчатых колес.
Таблица 2.6
Нормы точности зубчатых колес
| Степень точности по ГОСТ 1643–81 | Окружная скорость, м/с | |
| Прямые зубья | Непрямые зубья | |
| 5 и выше | 15 | 30 |
| 6 |  15 15 |  30 30 |
| 7 | 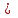 10 10 | 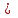 15 15 |
| 8 | 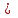 6 6 | 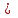 10 10 |
| 9 | 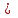 2 2 | 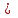 4 4 |
2.3. Проверочный расчет на контактную выносливость активных поверхностей зубьев
А. Определение расчетного контактного напряжения
Контактная выносливость устанавливается сопоставлением, действующим в полюсе зацепления расчетного и допускаемого контактного напряжений:
 , (2.26)
, (2.26)где KH – коэффициент нагрузки;
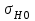 – контактное напряжение в полюсе зацепления при KH = 1.
– контактное напряжение в полюсе зацепления при KH = 1.Контактное напряжение в полюсе зацепления при KH = 1 определяют следующим образом, МПа:
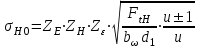 , (2.27)
, (2.27)где «+» – для наружного зацепления, «–» – для внутреннего зацепления;
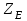 – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес. Для стали при модуле упругости
– коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес. Для стали при модуле упругости 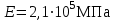
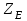 = 190;
= 190;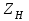 – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, определяют по табл. 2.7;
– коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, определяют по табл. 2.7;Таблица 2.7
Значения коэффициента
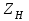
| Угол наклона линии зуба 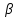 , град , град | Значения 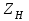 при относительном смещении контура при относительном смещении контура 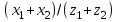 | | ||||||||||||
| | | 0,080 | 0,050 | 0,030 | 0,020 | 0,010 | 0,005 | 0 | –0,005 | –0,010 | –0,015 | –0,020 | ||
| | 0 | 1,48 | 1,52 | 1,58 | 1,62 | 1,68 | 1,71 | 1,76 | 1,83 | 1,93 | 2,14 | – | ||
| | 10 | 1,47 | 1,51 | 1,56 | 1,60 | 1,66 | 1,69 | 1,74 | 1,80 | 1,90 | 2,07 | – | ||
| | 15 | 1,46 | 1,50 | 1,55 | 1,58 | 1,63 | 1,67 | 1,71 | 1,77 | 1,86 | 2,00 | 2,35 | ||
| | 20 | 1,43 | 1,47 | 1,52 | 1,55 | 1,60 | 1,63 | 1,67 | 1,72 | 1,80 | 1,91 | 2,13 | ||
| | 25 | 1,42 | 1,45 | 1,49 | 1,52 | 1,57 | 1,59 | 1,62 | 1,67 | 1,73 | 1,81 | 1,97 | ||
| | 30 | 1,38 | 1,42 | 1,45 | 1,48 | 1,52 | 1,54 | 1,56 | 1,60 | 1,65 | 1,70 | 1,81 | ||
| | 35 | 1,35 | 1,37 | 1,40 | 1,42 | 1,46 | 1,48 | 1,50 | 1,53 | 1,56 | 1,60 | 1,66 | ||
| | 40 | 1,30 | 1,32 | 1,34 | 1,37 | 1,39 | 1,41 | 1,42 | 1,45 | 1,47 | 1,50 | 1,53 | ||
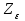 – коэффициент, учитывающий суммарную длину контактных линий;
– коэффициент, учитывающий суммарную длину контактных линий;FtH – окружная сила на делительном цилиндре, Н;
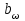 – рабочая ширина венца зубчатой передачи (b2), мм;
– рабочая ширина венца зубчатой передачи (b2), мм;d1 – делительный диаметр шестерни, мм.
Коэффициент
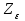 , учитывающий суммарную длину контактных линий, определяется следующим образом:
, учитывающий суммарную длину контактных линий, определяется следующим образом: 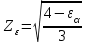 при
при 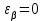 ;
;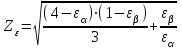 при
при 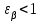 ; (2.28)
; (2.28)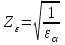 при
при 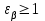 ,
,где
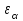 – коэффициент торцевого перекрытия:
– коэффициент торцевого перекрытия: 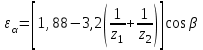 ;
;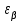 – коэффициент осевого перекрытия:
– коэффициент осевого перекрытия: 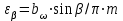 . (2.29)
. (2.29)Окружная сила на делительном цилиндре
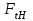 определяется по формуле
определяется по формуле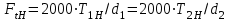 , (2.30)
, (2.30)где
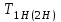 – вращающий момент на шестерне (колесе), Н · м;
– вращающий момент на шестерне (колесе), Н · м; 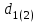 – делительный диаметр шестерни (колеса), мм.
– делительный диаметр шестерни (колеса), мм.Коэффициент нагрузки
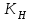 определяют по зависимости
определяют по зависимости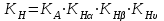 , (2.31)
, (2.31)где
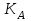 – коэффициент, учитывающий внешнюю динамическую нагрузку (табл. 2.8);
– коэффициент, учитывающий внешнюю динамическую нагрузку (табл. 2.8);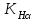 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;
– коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;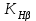 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба;
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба;