ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 99
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– предел текучести, МПа;
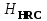 – твердость по шкале Роквелла;
– твердость по шкале Роквелла;
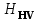 – твердость по шкале Виккерса.
– твердость по шкале Виккерса.
Расчетом определяют напряжение в опасном сечении на переходной поверхности зуба для каждого зубчатого колеса.
Расчет необходим для предотвращения усталостного излома зубьев. Устанавливается сопоставлением расчетного напряжения от изгиба в опасном сечении на переходной поверхности и допускаемого напряжения:
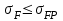 . (2.40)
. (2.40)
Расчетное напряжение при изгибе определяют по формуле
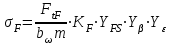 , (2.41)
, (2.41)
где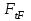 – окружная сила на делительном цилиндре, Н;
– окружная сила на делительном цилиндре, Н;
 – рабочая ширина зацепления зубчатой передачи, мм;
– рабочая ширина зацепления зубчатой передачи, мм;
m – нормальный модуль, мм;
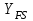 – коэффициент, учитывающий форму зуба и концентрацию напряжений;
– коэффициент, учитывающий форму зуба и концентрацию напряжений;
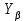 – коэффициент, учитывающий влияние наклона зуба;
– коэффициент, учитывающий влияние наклона зуба;
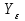 – коэффициент, учитывающий перекрытие зубьев;
– коэффициент, учитывающий перекрытие зубьев;
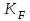 – коэффициент нагрузки.
– коэффициент нагрузки.
Окружная сила на делительном цилиндре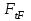 определяется по формуле
определяется по формуле
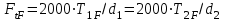 , (2.42)
, (2.42)
где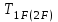 – вращающий момент на шестерне (колесе), Н · м;
– вращающий момент на шестерне (колесе), Н · м;
 – делительный диаметр шестерни (колеса), мм.
– делительный диаметр шестерни (колеса), мм.
Коэффициент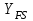 , учитывающий форму зуба и концентрацию напряжений, определяют по формуле:
, учитывающий форму зуба и концентрацию напряжений, определяют по формуле:
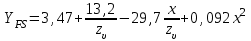 , (2.43)
, (2.43)
где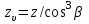 ;
;
x– коэффициент смещения, мм.
Коэффициент , учитывающий влияние угла наклона зубьев, определяется по формуле
, учитывающий влияние угла наклона зубьев, определяется по формуле
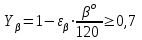 , (2.44)
, (2.44)
где значение угла подставляется в формулу в градусах;
подставляется в формулу в градусах;
 – коэффициент осевого перекрытия, который определяется по формуле
– коэффициент осевого перекрытия, который определяется по формуле 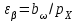 , где
, где 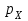 – осевой шаг:
– осевой шаг: 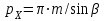 .
.
Полученное значение коэффициента должно находиться в пределах
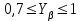 .
.
Коэффициент , учитывающий перекрытие зубьев, для косозубых передач определяют по формулам:
, учитывающий перекрытие зубьев, для косозубых передач определяют по формулам:
где – коэффициент торцевого перекрытия.
– коэффициент торцевого перекрытия.
Коэффициент нагрузки определяют по формуле
определяют по формуле
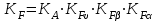 , (2.47)
, (2.47)
где – коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в циклограмме нагружения), – по табл. 2.8;
– коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в циклограмме нагружения), – по табл. 2.8;
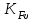 – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;
– коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;
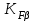 – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;
– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;
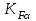 – коэффициент, учитывающий распределение нагрузки между зубьями.
– коэффициент, учитывающий распределение нагрузки между зубьями.
Коэффициент , учитывающий динамическую нагрузку, можно определить по формуле
, учитывающий динамическую нагрузку, можно определить по формуле
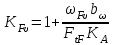 . (2.48)
. (2.48)
Все величины, входящие в формулу 2.48, найдены ранее, кроме F – удельной окружной динамической силы (Н/мм), которая может быть найдена по следующей зависимости:
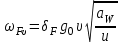 , (2.49)
, (2.49)
где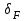 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев (для косозубых и шевронных передач
– коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев (для косозубых и шевронных передач 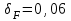 ; для прямозубых передач с модификацией головки
; для прямозубых передач с модификацией головки 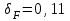 ; для прямозубых передач без модификации головки
; для прямозубых передач без модификации головки 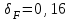 );
);
 – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, определяется по табл. 2.11 в зависимости от степени точности по нормам плавности и модуля зацепления.
– коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, определяется по табл. 2.11 в зависимости от степени точности по нормам плавности и модуля зацепления.
Найденная величина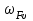 не должна превышать предельного значения, приведенного в табл. 2.15. В противном случае ее следует принимать равной предельному значению.
не должна превышать предельного значения, приведенного в табл. 2.15. В противном случае ее следует принимать равной предельному значению.
Таблица 2.15
Предельные значения удельной окружной динамической силы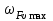
Коэффициент
, учитывающий неравномерность распределения нагрузки по длине контактных линий, определяется по графику, представленному на рис. 2.9, в зависимости от коэффициента и отношения
и отношения 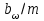 . Более точно коэффициент
. Более точно коэффициент  может быть определен по ГОСТ 21354–87.
может быть определен по ГОСТ 21354–87.
Коэффициент , учитывающий неравномерность распределения нагрузки между зубьями, определяется в зависимости от значения
, учитывающий неравномерность распределения нагрузки между зубьями, определяется в зависимости от значения  :
:
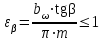 . (2.50)
. (2.50)
Если условие (2.41) выполняется, то коэффициент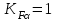 ; если не выполняется, то
; если не выполняется, то  определяется по следующей формуле:
определяется по следующей формуле:
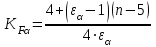 , (2.51)
, (2.51)
где n – степень точности по нормам контакта. Если n 9, то принимаем n = 9,
аналогично при n 5 принимаем n = 5;
 – коэффициент торцового перекрытия.
– коэффициент торцового перекрытия.
Между допускаемым напряжением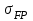 и пределом выносливости
и пределом выносливости 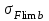 существует следующая взаимосвязь:
существует следующая взаимосвязь:
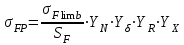 , (2.52)
, (2.52)
где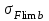 – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа;
– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа;
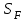 – коэффициент запаса прочности [см. приложение 1 табл. 1, 2, 3, 4];
– коэффициент запаса прочности [см. приложение 1 табл. 1, 2, 3, 4];
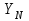
– коэффициент долговечности;
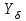 – коэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений;
– коэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений;
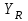 – коэффициент, учитывающий шероховатость переходной поверхности (выбираем в зависимости от вида обработки по табл. 2.13);
– коэффициент, учитывающий шероховатость переходной поверхности (выбираем в зависимости от вида обработки по табл. 2.13);
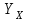 – коэффициент, учитывающий размеры зубчатого колеса.
– коэффициент, учитывающий размеры зубчатого колеса.
Коэффициент запаса прочности определяется в зависимости от способа термической и химико-термической обработки и вероятности неразрушения по таблицам прил. 1.
определяется в зависимости от способа термической и химико-термической обработки и вероятности неразрушения по таблицам прил. 1.
Коэффициент долговечности YNопределяют по формуле
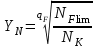 , но не менее 1, (2.53)
, но не менее 1, (2.53)
где qF – показатель степени;
NFlim – базовое число циклов перемены напряжений;
NК – суммарное число циклов перемены напряжений.
Для зубчатых колес с однородной структурой материала, включая закаленные при нагреве ТВЧ со сквозной закалкой, и со шлифованной переходной поверхностью независимо от твердости и термообработки их зубьев qF = 6.
Для зубчатых колес азотированных, а также цементированных и нитроцементированных с нешлифованной переходной поверхностью qF = 9.
Максимальные значения YN:
Базовое число циклов нагружения принимают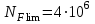 циклов. Под базовым числом циклов нагружения понимают число циклов, соответствующее на диаграмме усталости перехода наклонного участка кривой усталости в горизонтальный участок или участок с очень малым наклоном к оси циклов.
циклов. Под базовым числом циклов нагружения понимают число циклов, соответствующее на диаграмме усталости перехода наклонного участка кривой усталости в горизонтальный участок или участок с очень малым наклоном к оси циклов.
Суммарное число циклов перемены напряжений NК определяется по формуле 2.4.
Коэффициент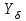 , учитывающий градиент напряжения и чувствительность материала к концентрации напряжений, находится в зависимости от значения модуля m по кривой (рис. 2.10).
, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений, находится в зависимости от значения модуля m по кривой (рис. 2.10).
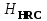 – твердость по шкале Роквелла;
– твердость по шкале Роквелла; 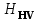 – твердость по шкале Виккерса.
– твердость по шкале Виккерса. 2.5. Расчет зубьев на выносливость при изгибе
А. Определение расчетного изгибного напряжения
Расчетом определяют напряжение в опасном сечении на переходной поверхности зуба для каждого зубчатого колеса.
Расчет необходим для предотвращения усталостного излома зубьев. Устанавливается сопоставлением расчетного напряжения от изгиба в опасном сечении на переходной поверхности и допускаемого напряжения:
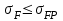 . (2.40)
. (2.40)Расчетное напряжение при изгибе определяют по формуле
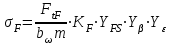 , (2.41)
, (2.41)где
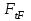 – окружная сила на делительном цилиндре, Н;
– окружная сила на делительном цилиндре, Н; – рабочая ширина зацепления зубчатой передачи, мм;
– рабочая ширина зацепления зубчатой передачи, мм;m – нормальный модуль, мм;
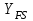 – коэффициент, учитывающий форму зуба и концентрацию напряжений;
– коэффициент, учитывающий форму зуба и концентрацию напряжений;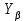 – коэффициент, учитывающий влияние наклона зуба;
– коэффициент, учитывающий влияние наклона зуба;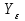 – коэффициент, учитывающий перекрытие зубьев;
– коэффициент, учитывающий перекрытие зубьев;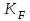 – коэффициент нагрузки.
– коэффициент нагрузки.Окружная сила на делительном цилиндре
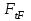 определяется по формуле
определяется по формуле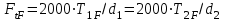 , (2.42)
, (2.42)где
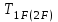 – вращающий момент на шестерне (колесе), Н · м;
– вращающий момент на шестерне (колесе), Н · м;  – делительный диаметр шестерни (колеса), мм.
– делительный диаметр шестерни (колеса), мм.Коэффициент
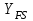 , учитывающий форму зуба и концентрацию напряжений, определяют по формуле:
, учитывающий форму зуба и концентрацию напряжений, определяют по формуле: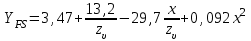 , (2.43)
, (2.43)
где
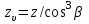 ;
;x– коэффициент смещения, мм.
Коэффициент
 , учитывающий влияние угла наклона зубьев, определяется по формуле
, учитывающий влияние угла наклона зубьев, определяется по формуле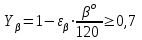 , (2.44)
, (2.44)где значение угла
 подставляется в формулу в градусах;
подставляется в формулу в градусах;  – коэффициент осевого перекрытия, который определяется по формуле
– коэффициент осевого перекрытия, который определяется по формуле 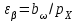 , где
, где 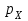 – осевой шаг:
– осевой шаг: 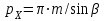 .
.Полученное значение коэффициента должно находиться в пределах
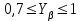 .
.Коэффициент
 , учитывающий перекрытие зубьев, для косозубых передач определяют по формулам:
, учитывающий перекрытие зубьев, для косозубых передач определяют по формулам:-
при
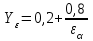 ,(2.45)
,(2.45) -
при
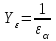 , (2.46)
, (2.46)
где
 – коэффициент торцевого перекрытия.
– коэффициент торцевого перекрытия. Коэффициент нагрузки
 определяют по формуле
определяют по формуле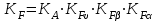 , (2.47)
, (2.47)где
 – коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в циклограмме нагружения), – по табл. 2.8;
– коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в циклограмме нагружения), – по табл. 2.8;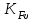 – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;
– коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;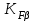 – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;
– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;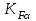 – коэффициент, учитывающий распределение нагрузки между зубьями.
– коэффициент, учитывающий распределение нагрузки между зубьями.
Коэффициент
 , учитывающий динамическую нагрузку, можно определить по формуле
, учитывающий динамическую нагрузку, можно определить по формуле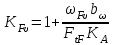 . (2.48)
. (2.48)Все величины, входящие в формулу 2.48, найдены ранее, кроме F – удельной окружной динамической силы (Н/мм), которая может быть найдена по следующей зависимости:
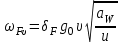 , (2.49)
, (2.49)где
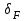 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев (для косозубых и шевронных передач
– коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев (для косозубых и шевронных передач 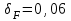 ; для прямозубых передач с модификацией головки
; для прямозубых передач с модификацией головки 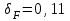 ; для прямозубых передач без модификации головки
; для прямозубых передач без модификации головки 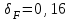 );
);  – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, определяется по табл. 2.11 в зависимости от степени точности по нормам плавности и модуля зацепления.
– коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, определяется по табл. 2.11 в зависимости от степени точности по нормам плавности и модуля зацепления. Найденная величина
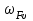 не должна превышать предельного значения, приведенного в табл. 2.15. В противном случае ее следует принимать равной предельному значению.
не должна превышать предельного значения, приведенного в табл. 2.15. В противном случае ее следует принимать равной предельному значению.Таблица 2.15
Предельные значения удельной окружной динамической силы
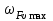
| Модуль m, мм | Степень точности по нормам плавности по ГОСТ 1643–81 | |||||
| 5 | 6 | 7 | 8 | 9 | 10 | |
 3,55 3,553,55…10 >10 | 85 105 150 | 160 194 250 | 240 310 450 | 380 410 590 | 700 880 1050 | 1200 1500 1800 |
Коэффициент

, учитывающий неравномерность распределения нагрузки по длине контактных линий, определяется по графику, представленному на рис. 2.9, в зависимости от коэффициента
 и отношения
и отношения 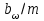 . Более точно коэффициент
. Более точно коэффициент  может быть определен по ГОСТ 21354–87.
может быть определен по ГОСТ 21354–87. 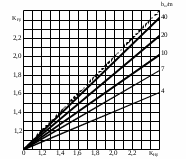 |
| Рис. 2.9. График для определения коэффициента  |
Коэффициент
 , учитывающий неравномерность распределения нагрузки между зубьями, определяется в зависимости от значения
, учитывающий неравномерность распределения нагрузки между зубьями, определяется в зависимости от значения  :
: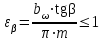 . (2.50)
. (2.50)Если условие (2.41) выполняется, то коэффициент
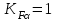 ; если не выполняется, то
; если не выполняется, то  определяется по следующей формуле:
определяется по следующей формуле: 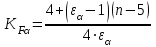 , (2.51)
, (2.51)где n – степень точности по нормам контакта. Если n 9, то принимаем n = 9,
аналогично при n 5 принимаем n = 5;
 – коэффициент торцового перекрытия.
– коэффициент торцового перекрытия. Б. Допускаемые напряжения в проверочном расчете на изгиб
Между допускаемым напряжением
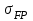 и пределом выносливости
и пределом выносливости 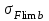 существует следующая взаимосвязь:
существует следующая взаимосвязь: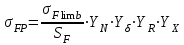 , (2.52)
, (2.52)где
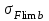 – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа;
– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа;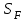 – коэффициент запаса прочности [см. приложение 1 табл. 1, 2, 3, 4];
– коэффициент запаса прочности [см. приложение 1 табл. 1, 2, 3, 4];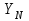
– коэффициент долговечности;
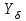 – коэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений;
– коэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений;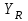 – коэффициент, учитывающий шероховатость переходной поверхности (выбираем в зависимости от вида обработки по табл. 2.13);
– коэффициент, учитывающий шероховатость переходной поверхности (выбираем в зависимости от вида обработки по табл. 2.13);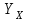 – коэффициент, учитывающий размеры зубчатого колеса.
– коэффициент, учитывающий размеры зубчатого колеса.Коэффициент запаса прочности
 определяется в зависимости от способа термической и химико-термической обработки и вероятности неразрушения по таблицам прил. 1.
определяется в зависимости от способа термической и химико-термической обработки и вероятности неразрушения по таблицам прил. 1.Коэффициент долговечности YNопределяют по формуле
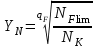 , но не менее 1, (2.53)
, но не менее 1, (2.53)где qF – показатель степени;
NFlim – базовое число циклов перемены напряжений;
NК – суммарное число циклов перемены напряжений.
Для зубчатых колес с однородной структурой материала, включая закаленные при нагреве ТВЧ со сквозной закалкой, и со шлифованной переходной поверхностью независимо от твердости и термообработки их зубьев qF = 6.
Для зубчатых колес азотированных, а также цементированных и нитроцементированных с нешлифованной переходной поверхностью qF = 9.
Максимальные значения YN:
-
YNmax= 4 при qF = 6; -
YNmax= 2,5 при qF = 9.
Базовое число циклов нагружения принимают
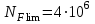 циклов. Под базовым числом циклов нагружения понимают число циклов, соответствующее на диаграмме усталости перехода наклонного участка кривой усталости в горизонтальный участок или участок с очень малым наклоном к оси циклов.
циклов. Под базовым числом циклов нагружения понимают число циклов, соответствующее на диаграмме усталости перехода наклонного участка кривой усталости в горизонтальный участок или участок с очень малым наклоном к оси циклов.Суммарное число циклов перемены напряжений NК определяется по формуле 2.4.
Коэффициент
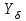 , учитывающий градиент напряжения и чувствительность материала к концентрации напряжений, находится в зависимости от значения модуля m по кривой (рис. 2.10).
, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений, находится в зависимости от значения модуля m по кривой (рис. 2.10).  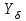 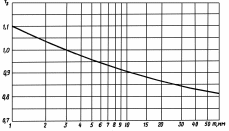 |
| Рис. 2.10. График для определения коэффициента 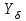 |