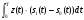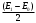Файл: Курсовая работа посвящена расчету и анализу основных характеристик простой дискретной системы связи. Системы связи предназначены для передачи информации в форме сообщения..docx
Добавлен: 23.11.2023
Просмотров: 157
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Структурная схема системы связи для передачи дискретных
5. Расчет характеристик системы согласно пункту 2.2
6. Описание процесса принятия решения при приеме сигнала
7. Расчет характеристик согласно пункту 2.3
Определение скорости передачи информации при наличии помех
9. Расчёт характеристик системы согласно пункту 2.4.
Расчет средней вероятности ошибки при когерентном приёме с использованием согласованного фильтра.
- модифицированная функция Бесселя нулевого порядка.
Рис.6. Условные плотности распределения гипотез, умноженные на априорные вероятности двоичных символов, при некогерентном приеме
Используя математический пакет MathCAD определим оптимальный порог :
:
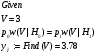
Таким образом,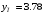 .
.
Условная вероятность ошибки первого рода равна:
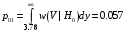
Условная вероятность ошибки второго рода равна:
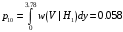
Средняя вероятность ошибки:
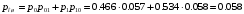
Наличие в канале помех (в данном случае гауссовского шума) вызывает ошибки при демодуляции и тем самым ограничивает скорость передачи информации: если ошибки следуют слишком часто, скорость передачи информации снижается, а если средняя вероятность ошибки достигает 0,5, скорость передачи становится равной нулю («обрыв канала»). Расчет скорости передачи информации в цифровом канале с помехами основывается на понятии совместной энтропии входа и выхода канала (под каналом здесь следует понимать отрезок системы связи от входа модулятора до выхода демодулятора).
На входе модулятора действует источник, алфавит которого (обозначим его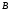 ) содержит два символа –
) содержит два символа – 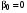 и
и 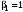 . Априорными вероятностями этих символов
. Априорными вероятностями этих символов 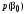 и
и 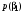 следует считать, очевидно, вероятности нуля
следует считать, очевидно, вероятности нуля 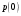 и единицы
и единицы  , рассчитанные при выполнении пункта 2.2 задания. Выход демодулятора можно считать другим источником
, рассчитанные при выполнении пункта 2.2 задания. Выход демодулятора можно считать другим источником 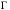 с двумя символами
с двумя символами 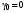 и
и 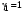 . Среднее количество передаваемой по каналу информации (приходящееся на один символ) равно:
. Среднее количество передаваемой по каналу информации (приходящееся на один символ) равно:
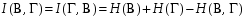
Для определения совместной энтропии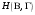 необходимо найти совместные вероятности всех сочетаний входных и выходных символов (
необходимо найти совместные вероятности всех сочетаний входных и выходных символов (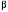 и
и 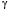
), а для этого нужно вначале записать условные вероятности для выходных символов при заданных входных. Эти условные вероятности определяются, в свою очередь, условными вероятностями ошибок первого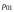 и второго
и второго 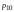 рода, рассчитанными ранее (отдельно для когерентного и некогерентного приема):
рода, рассчитанными ранее (отдельно для когерентного и некогерентного приема):
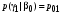 ;
;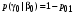 ;
;
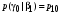 ;
; 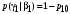 .
.
Совместные вероятности сочетаний входных и выходных символов:
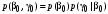 ;
; 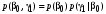 ;
;
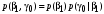 ;
; 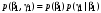 .
.
Для нахождения энтропии источника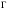 требуются безусловные вероятности выходных символов:
требуются безусловные вероятности выходных символов:
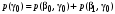
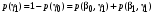 .
.
Наконец, совместная энтропия входа и выхода цифрового канала:
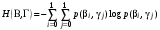 .
.
Скорость передачи информации по цифровому каналу с учетом помех:
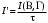 ,где
,где  – длительность посылки.
– длительность посылки.
Произведем расчеты
Условные вероятности всех сочетаний входных и выходных символов:
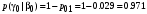
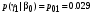
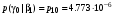
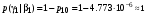
Совместные вероятности сочетаний входных и выходных символов:
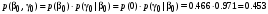
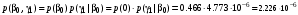
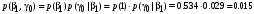
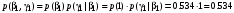
Безусловные вероятности выходных символов:
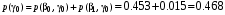
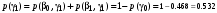
Совместная энтропия входа и выхода цифрового канала: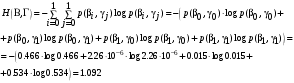
Энтропия источника на выходе цифрового канала:
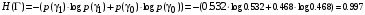 Энтропия источника на входе цифрового канала:
Энтропия источника на входе цифрового канала:
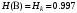
Среднее количество передаваемой по каналу информации (приходящееся на один символ)
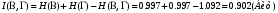
Скорость передачи информации по цифровому каналу с учетом помех:
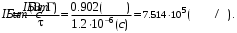
Условные вероятности всех сочетаний входных и выходных символов:
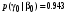
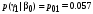
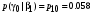
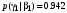
Совместные вероятности сочетаний входных и выходных символов:
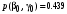
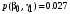
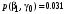
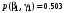
Безусловные вероятности выходных символов:
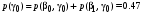
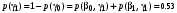
Совместная энтропия входа и выхода цифрового канала:
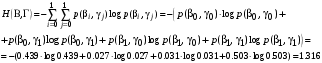
Энтропия источника на выходе цифрового канала:
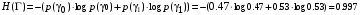 Энтропия источника на входе цифрового канала:
Энтропия источника на входе цифрового канала:

Среднее количество передаваемой по каналу информации (приходящееся на один символ)
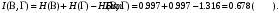
Скорость передачи информации по цифровому каналу с учетом помех:
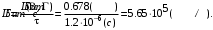
Скорость передачи информации по цифровому каналу с учетом помех при когерентном приеме сигнала выше, так как при некогерентном приеме сигнала теряется часть информации, которая заложена в начальной фазе и нам неизвестна. Средняя вероятность ошибки меньше при когерентном приеме
Для принятия решающим устройством решения о пришедших из линии связи сигнале или паузе нужно вычислить корреляционный интеграл, а затем проверить неравенство:
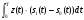
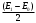
Рис.6. Условные плотности распределения гипотез, умноженные на априорные вероятности двоичных символов, при некогерентном приеме
Используя математический пакет MathCAD определим оптимальный порог
 :
: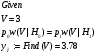
Таким образом,
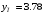 .
.Условная вероятность ошибки первого рода равна:
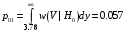
Условная вероятность ошибки второго рода равна:
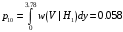
Средняя вероятность ошибки:
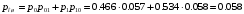
Определение скорости передачи информации при наличии помех
Наличие в канале помех (в данном случае гауссовского шума) вызывает ошибки при демодуляции и тем самым ограничивает скорость передачи информации: если ошибки следуют слишком часто, скорость передачи информации снижается, а если средняя вероятность ошибки достигает 0,5, скорость передачи становится равной нулю («обрыв канала»). Расчет скорости передачи информации в цифровом канале с помехами основывается на понятии совместной энтропии входа и выхода канала (под каналом здесь следует понимать отрезок системы связи от входа модулятора до выхода демодулятора).
На входе модулятора действует источник, алфавит которого (обозначим его
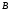 ) содержит два символа –
) содержит два символа – 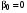 и
и 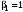 . Априорными вероятностями этих символов
. Априорными вероятностями этих символов 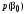 и
и 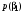 следует считать, очевидно, вероятности нуля
следует считать, очевидно, вероятности нуля 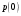 и единицы
и единицы  , рассчитанные при выполнении пункта 2.2 задания. Выход демодулятора можно считать другим источником
, рассчитанные при выполнении пункта 2.2 задания. Выход демодулятора можно считать другим источником 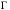 с двумя символами
с двумя символами 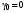 и
и 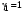 . Среднее количество передаваемой по каналу информации (приходящееся на один символ) равно:
. Среднее количество передаваемой по каналу информации (приходящееся на один символ) равно: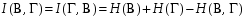
Для определения совместной энтропии
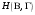 необходимо найти совместные вероятности всех сочетаний входных и выходных символов (
необходимо найти совместные вероятности всех сочетаний входных и выходных символов (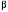 и
и 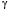
), а для этого нужно вначале записать условные вероятности для выходных символов при заданных входных. Эти условные вероятности определяются, в свою очередь, условными вероятностями ошибок первого
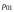 и второго
и второго 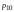 рода, рассчитанными ранее (отдельно для когерентного и некогерентного приема):
рода, рассчитанными ранее (отдельно для когерентного и некогерентного приема):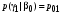 ;
;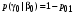 ;
;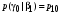 ;
; 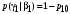 .
.Совместные вероятности сочетаний входных и выходных символов:
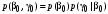 ;
; 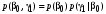 ;
;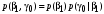 ;
; 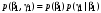 .
.Для нахождения энтропии источника
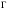 требуются безусловные вероятности выходных символов:
требуются безусловные вероятности выходных символов: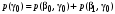
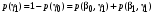 .
.Наконец, совместная энтропия входа и выхода цифрового канала:
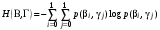 .
.Скорость передачи информации по цифровому каналу с учетом помех:
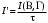 ,где
,где  – длительность посылки.
– длительность посылки.Произведем расчеты
Для когерентного приема
Условные вероятности всех сочетаний входных и выходных символов:
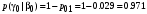
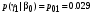
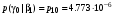
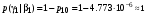
Совместные вероятности сочетаний входных и выходных символов:
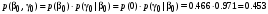
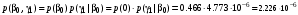
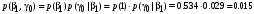
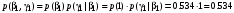
Безусловные вероятности выходных символов:
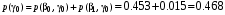
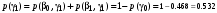
Совместная энтропия входа и выхода цифрового канала:
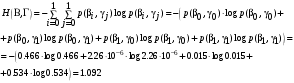
Энтропия источника на выходе цифрового канала:
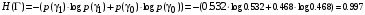 Энтропия источника на входе цифрового канала:
Энтропия источника на входе цифрового канала: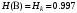
Среднее количество передаваемой по каналу информации (приходящееся на один символ)
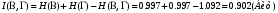
Скорость передачи информации по цифровому каналу с учетом помех:
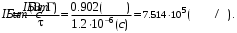
Для некогерентного приема
Условные вероятности всех сочетаний входных и выходных символов:
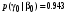
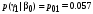
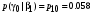
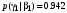
Совместные вероятности сочетаний входных и выходных символов:
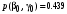
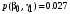
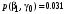
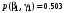
Безусловные вероятности выходных символов:
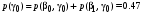
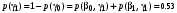
Совместная энтропия входа и выхода цифрового канала:

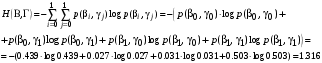
Энтропия источника на выходе цифрового канала:
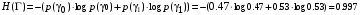 Энтропия источника на входе цифрового канала:
Энтропия источника на входе цифрового канала:
Среднее количество передаваемой по каналу информации (приходящееся на один символ)
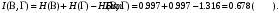
Скорость передачи информации по цифровому каналу с учетом помех:
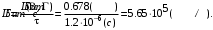
Скорость передачи информации по цифровому каналу с учетом помех при когерентном приеме сигнала выше, так как при некогерентном приеме сигнала теряется часть информации, которая заложена в начальной фазе и нам неизвестна. Средняя вероятность ошибки меньше при когерентном приеме
8. Описание принципа корреляционной обработки и согласованной фильтрации; расчёт согласованного фильтра
Для принятия решающим устройством решения о пришедших из линии связи сигнале или паузе нужно вычислить корреляционный интеграл, а затем проверить неравенство: