Файл: Курсовая работа посвящена расчету и анализу основных характеристик простой дискретной системы связи. Системы связи предназначены для передачи информации в форме сообщения..docx
Добавлен: 23.11.2023
Просмотров: 151
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Структурная схема системы связи для передачи дискретных
5. Расчет характеристик системы согласно пункту 2.2
6. Описание процесса принятия решения при приеме сигнала
7. Расчет характеристик согласно пункту 2.3
Определение скорости передачи информации при наличии помех
9. Расчёт характеристик системы согласно пункту 2.4.
Расчет средней вероятности ошибки при когерентном приёме с использованием согласованного фильтра.
Демодулятор выделяет огибающую ВЧ колебаний, пришедших с канала связи и, сравнивая уровень поступившего сигнала с пороговым, различает принятые сигналы, т.е. на декодер подаются кодовые комбинации. На выходе декодера приёмник информации получает сигнал 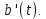
Экономное (статистическое, энтропийное) кодирование основано на очень простой идее: чем чаще в сообщениях данного источника встречается некоторый символ, тем короче должна быть соответствующая ему кодовая комбинация. Некоторые коды, называемые примитивными, не учитывают статистических свойств источника; таков, например, известный код Бодо, все комбинации которого имеют равную длину. Такие коды называют равномерными. Очевидно, статистический код должен быть неравномерным.
Кодирование источника по методу Хаффмена
Принцип построения кода Хаффмена состоит в упорядочении всех символов алфавита по убыванию априорных вероятностей. Затем две нижние буквы соединяются скобкой, верхней присваивается единица, нижней – ноль, так как значение априорной вероятности первой из них больше чем второй. Вычисляется суммарная вероятность этих двух символов. Все буквы снова записываются в порядке убывания вероятностей, при этом только что рассмотренные буквы «склеиваются», т.е. учитываются как единая буква с суммарной вероятностью. Повторяются шаги нахождения двух наименьших значений вероятности и их «склеивания». Эта процедура продолжается до тех пор, пока не останется ни одной буквы, не охваченной скобкой.
Таблица 3
Кодирование символов алфавита кодом Хаффмена, длины кодовых комбинаций
Таблица 4
Таким образом, символы алфавита представляются следующими кодовыми комбинациями (см.табл.5).
Таблица 5
Кодовые комбинации
Кодирование построенным кодом фамилии и имени исполнителя курсовой работы.
Закодируем фразу: КАЗАКОВ ДМИТРИЙ. Отсутствующие в алфавите источника буквы пропускаются:
КААКОВ ДМИРИ.
Получившийся код (см.табл.6):
Таблица 6
Временные диаграммы сигнала (отвечающего первым двум буквам сообщения) в промежуточных точках схемы:
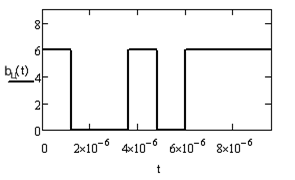
Рис.2. Фрагмент сигнала на выходе кодера
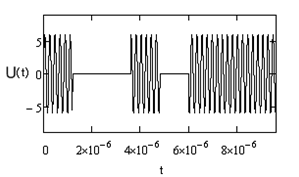
Рис.3. Фрагмент сигнала на выходе модулятора.
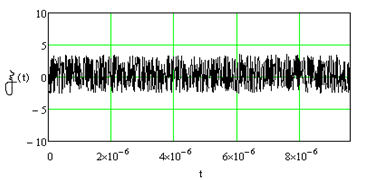
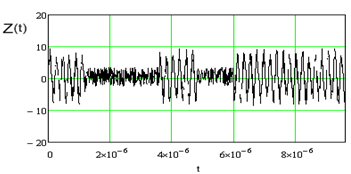
Рис.4. 1- Шум, 2- Фрагмент сигнала на входе демодулятора.
Информационная производительность дискретного источника характеризуется средним количеством информации на символ, которое определяется как математическое ожидание этой случайной величины. В случае источника без памяти, среднее количество информации, приходящееся на один символ и называемое энтропией дискретного источника А, определяется как:


Максимальную производительность при заданном объеме алфавита имеет источник с равновероятными символами, т.е. при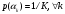 .
.
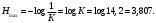
Для того чтобы выразить степень отличия производительности источника от максимально достижимой при заданном объеме алфавита, вводят числовой коэффициент, называемой избыточностью:
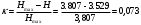
Избыточность характеризует возможность сжатия сообщений данного источника и повышения скорости передачи информации посредством статистического кодирования. Очевидно, избыточность может принимать значения от 0 до 1, и возможность сжатия тем выше, чем больше величина .
.
Средняя длина кодовой комбинации для построенного кода:
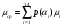
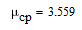
Согласно теореме Шеннона при оптимальном кодировании можно достичь средней длины:
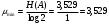
Определим вероятности появления двоичных символов в кодовой комбинации. Очевидно, эти вероятности можно найти следующим образом: а) подсчитать количества единиц (или нулей) во всех кодовых словах; б) умножить эти количества на вероятности соответствующих кодовых слов; в)
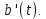
4. Описание принципов кодирования источника при передаче дискретных сообщений. Построение кода. Кодирование построенным кодом фамилии и имени исполнителя курсовой работы.
Экономное (статистическое, энтропийное) кодирование основано на очень простой идее: чем чаще в сообщениях данного источника встречается некоторый символ, тем короче должна быть соответствующая ему кодовая комбинация. Некоторые коды, называемые примитивными, не учитывают статистических свойств источника; таков, например, известный код Бодо, все комбинации которого имеют равную длину. Такие коды называют равномерными. Очевидно, статистический код должен быть неравномерным.
Кодирование источника по методу Хаффмена
Принцип построения кода Хаффмена состоит в упорядочении всех символов алфавита по убыванию априорных вероятностей. Затем две нижние буквы соединяются скобкой, верхней присваивается единица, нижней – ноль, так как значение априорной вероятности первой из них больше чем второй. Вычисляется суммарная вероятность этих двух символов. Все буквы снова записываются в порядке убывания вероятностей, при этом только что рассмотренные буквы «склеиваются», т.е. учитываются как единая буква с суммарной вероятностью. Повторяются шаги нахождения двух наименьших значений вероятности и их «склеивания». Эта процедура продолжается до тех пор, пока не останется ни одной буквы, не охваченной скобкой.
Таблица 3
| и | ж | н | е | р | о | а | в | б | к | д | м | с | п |
| 0,102 | 0,074 | 0,067 | 0,092 | 0,167 | 0,014 | 0,064 | 0,064 | 0,102 | 0,028 | 0,085 | 0,026 | 0,131 | 0,014 |
Кодирование символов алфавита кодом Хаффмена, длины кодовых комбинаций
Таблица 4
| Символ и его вероятность | Комбинации кодовых слов Разряды | Длина комбинации | Число «1» | Число «0» | |||||||
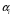 | 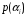 | 1 | 2 | 3 | 4 | 5 | 6 | 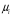 | 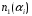 | 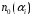 | |
| о | 0,014 | 1 | 1 | 1 | | | | 3 | 3 | 0 | |
| п | 0,014 | 1 | 1 | 1 | | | | 3 | 2 | 1 | |
| м | 0,026 | 1 | 0 | 1 | | | | 3 | 2 | 1 | |
| к | 0,028 | 0 | 1 | 1 | | | | 3 | 2 | 1 | |
| а | 0,064 | 0 | 0 | 0 | | | | 3 | 0 | 3 | |
| в | 0,064 | 0 | 1 | 0 | 1 | | | 4 | 2 | 2 | |
| н | 0,067 | 0 | 1 | 0 | 0 | | | 4 | 1 | 3 | |
| ж | 0,074 | 0 | 0 | 1 | 1 | | | 4 | 2 | 2 | |
| д | 0,085 | 0 | 0 | 1 | 0 | | | 4 | 1 | 3 | |
| е | 0,092 | 1 | 0 | 0 | 1 | 1 | | 5 | 3 | 2 | |
| и | 0,102 | 1 | 0 | 0 | 0 | 1 | | 5 | 2 | 3 | |
| б | 0,102 | 1 | 0 | 0 | 0 | 0 | | 5 | 1 | 4 | |
| с | 0,131 | 1 | 0 | 0 | 1 | 0 | 1 | 6 | 3 | 3 | |
| р | 0,167 | 1 | 0 | 0 | 1 | 0 | 0 | 6 | 2 | 4 | |
Таким образом, символы алфавита представляются следующими кодовыми комбинациями (см.табл.5).
Таблица 5
Кодовые комбинации
| 0 | 111 |
| П | 110 |
| М | 101 |
| К | 011 |
| А | 000 |
| В | 0101 |
| Н | 0100 |
| Ж | 0011 |
| Д | 0010 |
| Е | 10011 |
| И | 10001 |
| Б | 10000 |
| С | 100101 |
| р | 100100 |
Кодирование построенным кодом фамилии и имени исполнителя курсовой работы.
Закодируем фразу: КАЗАКОВ ДМИТРИЙ. Отсутствующие в алфавите источника буквы пропускаются:
КААКОВ ДМИРИ.
Получившийся код (см.табл.6):
Таблица 6
| К | А | А | К | О | В | Д | М | И | Р | И |
| 011 | 000 | 000 | 011 | 111 | 0101 | 0010 | 101 | 10001 | 100100 | 10001 |
Временные диаграммы сигнала (отвечающего первым двум буквам сообщения) в промежуточных точках схемы:

Рис.2. Фрагмент сигнала на выходе кодера

Рис.3. Фрагмент сигнала на выходе модулятора.


Рис.4. 1- Шум, 2- Фрагмент сигнала на входе демодулятора.
5. Расчет характеристик системы согласно пункту 2.2
Информационная производительность дискретного источника характеризуется средним количеством информации на символ, которое определяется как математическое ожидание этой случайной величины. В случае источника без памяти, среднее количество информации, приходящееся на один символ и называемое энтропией дискретного источника А, определяется как:

Максимальную производительность при заданном объеме алфавита имеет источник с равновероятными символами, т.е. при
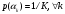 .
.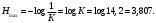
Для того чтобы выразить степень отличия производительности источника от максимально достижимой при заданном объеме алфавита, вводят числовой коэффициент, называемой избыточностью:
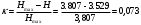
Избыточность характеризует возможность сжатия сообщений данного источника и повышения скорости передачи информации посредством статистического кодирования. Очевидно, избыточность может принимать значения от 0 до 1, и возможность сжатия тем выше, чем больше величина
 .
.Средняя длина кодовой комбинации для построенного кода:
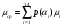
Согласно теореме Шеннона при оптимальном кодировании можно достичь средней длины:
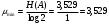
Определим вероятности появления двоичных символов в кодовой комбинации. Очевидно, эти вероятности можно найти следующим образом: а) подсчитать количества единиц (или нулей) во всех кодовых словах; б) умножить эти количества на вероятности соответствующих кодовых слов; в)