Файл: Курсовая работа посвящена расчету и анализу основных характеристик простой дискретной системы связи. Системы связи предназначены для передачи информации в форме сообщения..docx
Добавлен: 23.11.2023
Просмотров: 145
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Структурная схема системы связи для передачи дискретных
5. Расчет характеристик системы согласно пункту 2.2
6. Описание процесса принятия решения при приеме сигнала
7. Расчет характеристик согласно пункту 2.3
Определение скорости передачи информации при наличии помех
9. Расчёт характеристик системы согласно пункту 2.4.
Расчет средней вероятности ошибки при когерентном приёме с использованием согласованного фильтра.
В случае системы с пассивной паузой:
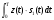
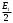
В корреляционном приемнике такой интеграл формируется при помощи перемножителей и интеграторов. Если в системе передачи информации используется много сигналов, то для каждого из этих сигналов нужно генерировать опорный сигнал с точностью до начальной фазы, на что нужно большое число корреляторов и интеграторов. Поэтому возникает желание заменить корреляционную обработку фильтровой, т.е. вычислять корреляционный интеграл при помощи ЛИС-цепи.
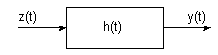
Рис.7. Структурная схема ЛИС-цепи
Импульсной характеристикой h(t) называется функция, являющаяся откликом цепи на входной в виде δ(t). Физически – импульсная характеристика приближенно отображает реакцию цепи на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временным масштабом цепи, например, периодом ее собственных колебаний.
Сигнал y(t) на выходе ЛИС-цепи будет определяться интегралом Дюамеля:
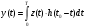
Считая сигнал полностью известным, добиться корреляционного интеграла на выходе согласованного фильтра можем, положив равенство:
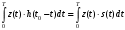
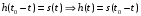
АЧХ согласованного фильтра в идеале должно иметь такую же форму, как и модуль спектральной плотности сигнала.
Пусть на фильтр подается сигнал:
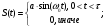
с импульсной характеристикой:
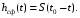
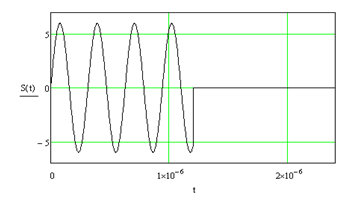
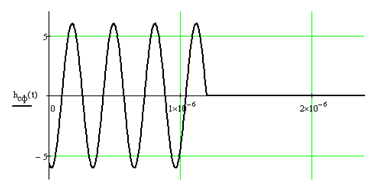
Рис.8. Графики сигнала, подаваемого на фильтр, и импульсной характеристики
согласованного фильтра
Комплексно- частотная характеристика согласованного фильтра рассчитывается по формуле:
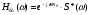
Ниже приведем графики амплитудно- и фазо-частотной характеристик фильтра:
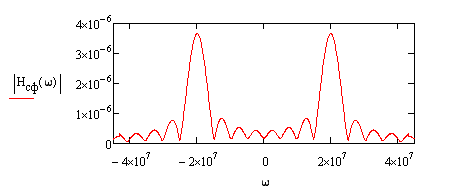
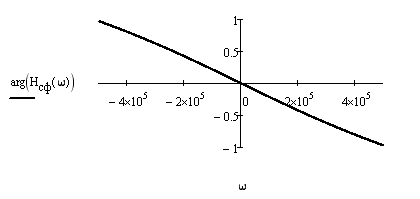
Рис.9. АЧХ и ФЧХ согласованного фильтра
При согласованной фильтрации усиливаются сильные составляющие сигнала и подавляются слабые.
9. Расчёт характеристик системы согласно пункту 2.4.
На вход СФ поступает радиоимпульс, длительностью элементарной посылки:
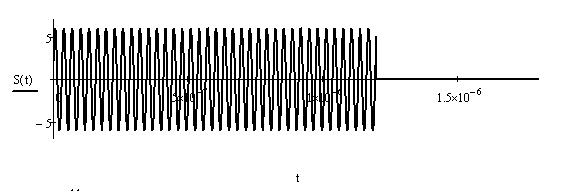
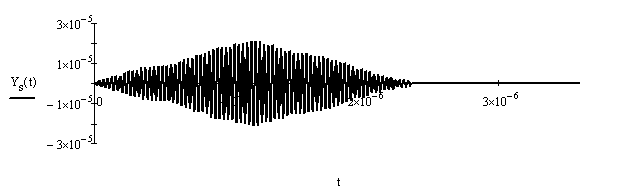
Рис.10. Сигнал на входе и на выходе СФ.
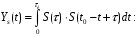
Вычисляя интеграл, получим сигнал на выходе согласованного фильтра. Фактически, это будет взаимнокорреляционная функция входного сигнала S (t), сдвинутая вправо на его длительность. Основное свойство взаимнокорреляционной функции в том, что её максимум численно равен энергии сигнала.
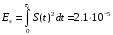
Максимум выходного сигнала достигается при t =τ.
Форма выходного сигнала сильно изменилась по сравнению с входным, но для нас важна не форма сигнала, а отношение выделяемой им мощности к мощности помехи, которая тоже прошла через фильтр. Так как фильтр согласован с сигналом, то модуль его передаточной функции равен модулю спектральной плотности сигнала на входе, а это значит, что согласованный фильтр пропускает сильно выраженные гармоники сигнала и не пропускает слабо выраженные гармоники.
Для дальнейших расчетов определим ДИСПЕРСИЮ на выходе из фильтра:
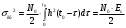
Из выражений:
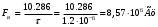 и
и 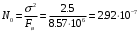 поскольку мы учитываем, что шум на входе СФ квазибелый с полосой (-F;F), содержащий 99% энергии сигнала,
поскольку мы учитываем, что шум на входе СФ квазибелый с полосой (-F;F), содержащий 99% энергии сигнала, 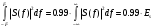
Получаем :
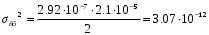
Расчет средней вероятности ошибки при когерентном приёме с использованием согласованного фильтра.
Запишем плотности распределения вероятности двух гипотез:
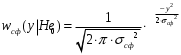
- условная ПРВ для гипотезы Н0 (только шум на выходе СФ)
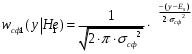 - условная ПРВ для гипотезы Н1 (сигнал + шум на выходе СФ)
- условная ПРВ для гипотезы Н1 (сигнал + шум на выходе СФ)Теперь вычислим порог принятия решения уП , приравнивая эти плотности распределения и домножая на вероятности «0» и «1» соответственно:
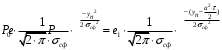
Решив уравнение, получим:
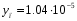
Найдем вероятность ошибки первого и второго рода и среднюю вероятность ошибки при когерентном приеме на выходе согласованного фильтра:

Р01=0, Р10=0, Рош=Р0. Р01 + Р1.Р10 = 0 -нулевая средняя вероятность ошибки при когерентном приеме на выходе согласованного фильтра.
Найдем выигрыш в отношении сигнал/ шум за счет согласованного фильтра равен:
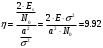
1
 0.11. Описание принципов помехоустойчивого кодирования при передаче дискретных сообщений. Построение (7,4)- кода Хемминга. Расчет характеристик согласно п.2.5
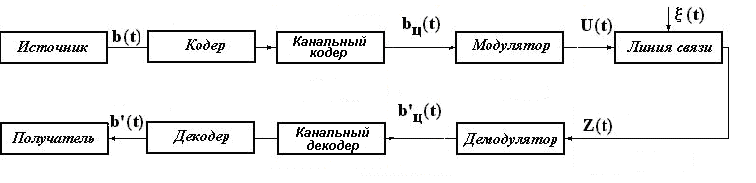
0.11. Описание принципов помехоустойчивого кодирования при передаче дискретных сообщений. Построение (7,4)- кода Хемминга. Расчет характеристик согласно п.2.5 Рис.11. Обобщенная структурная схема системы связи, использующая помехоустойчивое кодирование
Основное отличие системы связи для передачи дискретных сообщений с помехоустойчивым кодированием от системы связи для передачи дискретных сообщений состоит в наличие помимо кодера (декодера), источника ещё и канального кодера (декодера).
Кодер источника – сокращает избыточность источника сообщения для более рационального использования канала связи. Потери информации не происходит.
Декодер источника – обратные операции к кодеру источника (представление данных в удобном для потребителя виде)
Канальный кодер – повышение помехоустойчивости путем введения дополнительной избыточности.
Канальный декодер – операции обратные канальному кодеру.
Канальный декодер принимает символы кодового алфавита и вычисляет контрольные символы. Если контрольные символы, вычисленные приемником, не совпадут с принятыми контрольными символами, то приёмник отмечает ошибку. Канальный декодер также вычисляет синдром ошибки, указывающий на номер разряда, в котором произошла ошибка (если ошибка произошла только в одном разделе) в принимаемой кодовой комбинации.
Принцип кода Хемминга состоит в том, что путем преобразования нескольких контрольных разрядов удается не только обнаружить единичную ошибку, но и локализовать ее. Если для двоичного кода определяется точное расположение неправильного разряда, то его можно скорректировать путем инвертирования.
Помехоустойчивое кодирование предназначено для обнаружения и исправления ошибок, примешиваемых к сигналу в канале связи. Экономное кодирование направлено на сокращение избыточности источника, а помехоустойчивое – наоборот приводит к увеличению избыточности и, следовательно, к снижению скорости передачи. Но в то же время при экономном кодировании и сильных помехах в канале связи велика вероятность принятия ошибочного решения, а при использовании помехоустойчивого кодирования, эта вероятность существенно меньше.
Итак, цель помехоустойчивого кодирования – увеличение помехоустойчивости путем введения избыточности кода.
Коды Хемминга представляют собой (n, k)-коды, удовлетворяющие условию:
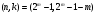
при некотором целом m.
Для (7,4)-кода порождающая матрица кода:

Построим канальный код (7,4). Для этого сначала разобьем построенную фразу на равные части по четыре символа:
Фраза:
КАЗАКОВ ДМИТРИЙ.
011 000 000 011 111 0101 0010 101 10001 100100 10001
После разбиения получилось:
1001 0011 1010 0100 1001 0010 0100 0110 0011 0010 0000
Так как строчка неполная оказалась, я добавила символы 000
В виде матрицы Х представим информационные символы:
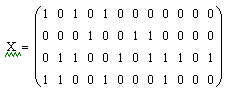
Матрица кодирования будет вычисляться по формуле:
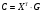
Матрица кодирования:
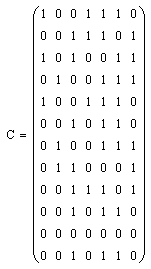
Предположим, что передавалась комбинация (0100111), и при передаче произошла ошибка во втором символе: (0000111) – принятая комбинация.
С помощью проверочной матрицы (Нт) найдем ошибку: