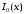Файл: Курсовая работа посвящена расчету и анализу основных характеристик простой дискретной системы связи. Системы связи предназначены для передачи информации в форме сообщения..docx
Добавлен: 23.11.2023
Просмотров: 155
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Структурная схема системы связи для передачи дискретных
5. Расчет характеристик системы согласно пункту 2.2
6. Описание процесса принятия решения при приеме сигнала
7. Расчет характеристик согласно пункту 2.3
Определение скорости передачи информации при наличии помех
9. Расчёт характеристик системы согласно пункту 2.4.
Расчет средней вероятности ошибки при когерентном приёме с использованием согласованного фильтра.
просуммировать полученные величины;
г) отнести результат к средней длине кодового слова.
Таким образом:
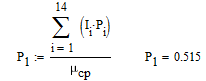
Энтропия кода находится как энтропия случайной величины, принимающей два значения (0 и 1) с вероятностями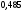
и 
:
И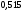збыточность кода:
где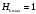
- максимальная энтропия двоичного кода.
Скорость передачи информации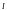
по каналу без помех определяется только временем передачи одного кодового символа (равным длительности посылки 
), средней длиной кодового слова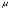 
и средним количеством информации, заключенной в кодовом слове, равным энтропии 
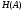исходного источника. Нетрудно видеть, что
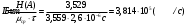
В данной курсовой работе рассматривается задача построения оптимального демодулятора (приемника) для случая амплитудной телеграфии с пассивной паузой, что соответствует принятию решения о том, что передавался символ 0 (сигнала нет) или символ 1 (сигнал есть). Таким образом, решается задача обнаружения сигнала в наблюдаемом колебании. В работе предполагается, что помеха в канале представляет собой гауссовский шум с нулевым средним и известной дисперсией, который взаимодействует с сигналом аддитивно (суммируется). Результатом обработки наблюдаемого колебания является случайная величина
y , которая может иметь различное распределение в зависимости от того, есть ли сигнал в наблюдаемом колебании, а именно: распределение при гипотезе H0 – «сигнала нет» – является гауссовским с нулевым средним, а распределение при гипотезе H1 – «сигнал есть» – отличается сдвигом на величину a, зависящую от способа обработки (в данном случае амплитуда несущего колебания). Значение a предполагается известным. Таким образом, проверяемые гипотезы описываются двумя условнымиплотностями распределения вероятностей w(y |H0) и w(y | H1).
В данной постановке демодулятор (приемник) может принимать решение, основываясь только на наблюдаемом значении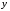
: очевидно, чем больше наблюдаемое значение, тем с большей уверенностью можно утверждать, что сигнал в принятом колебании есть. Приемник в таком случае должен сравнить 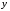с некоторым фиксированным значением (порогом) 
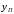и если 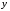больше порога, принять решение о наличии сигнала, в противном
случае – о его отсутствии, что можно кратко записать в следующей символической форме:
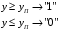
Когерентным приемом или приемом полностью известного сигнала называется принятие решения в системе связи при следующих условиях: синхронизация является точной и форма сигнала на интервале наблюдения точно известна, неизвестен лишь сам факт наличия либо отсутствия сигнала в наблюдаемом колебании. (Эта ситуация наиболее близка к реальности в кабельных линиях связи, где условия распространения сигналов известны и практически неизменны.)
Как было сказано в пункте 6, принимаемое демодулятором решение основывается на сравнении значения наблюдаемой реализации с некоторым фиксированным (пороговым) значением
.
Условные плотности распределения проверяемых приемником гипотез имеют вид:
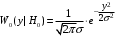для гипотезы 
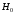- «сигнала нет»;
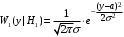для гипотезы 
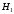- «сигнала есть»;
где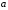
- амплитуда сигнала и 
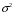- дисперсия шума даны.
Каким бы ни был порог , очевидно, есть некоторая ненулевая вероятность 
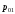принять решение о наличии сигнала при его фактическом отсутствии. Эта вероятность называется условной вероятностью ошибки первого рода («ложной тревоги») и определяется выражением:
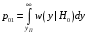
Аналогично, существует ненулевая вероятность принять решение об отсутствии сигнала, в то время как на самом деле он есть (условная вероятность ошибки второго рода, или пропуска сигнала):
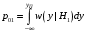
Очевидно, сумма указанных условных вероятностей минимальна, если порог находится как абсцисса точки пересечения условных плотносте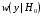й:
и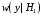 
При таком выборе порога приемник является оптимальным по критерию минимума суммарной условной вероятности ошибки. В нашем случае, априорные вероятности проверяемых гипотез различны, поэтому мы переходим к критерию идеального наблюдателя (к построению оптимального байесовского приемника, обеспечивающего минимальную среднюю вероятность ошибки). В этом случае оптимальный порог выбирается из условия:
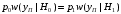
где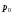
и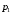 
- априорные вероятности гипотез.
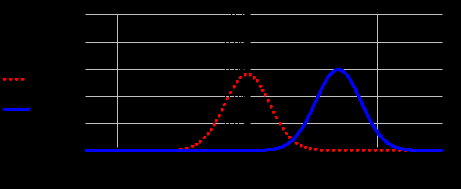
Рис.5. Условные плотности распределения гипотез, умноженные на априорные вероятности двоичных символов, при когерентном приеме
Используя математический пакет MathCAD определим оптимальный порог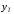
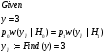
Таким образом,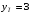
.
Значит, условная вероятность ошибки первого рода равна:
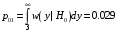
Условная вероятность ошибки второго рода равна:
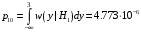
Средняя вероятность ошибки:
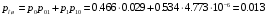
Случай точно известного сигнала на практике является скорее исключением. Обычно некоторые параметры сигнала на приемной стороне канала связи неизвестны. В курсовой работе рассматривается прием сигнала, имеющего форму прямоугольного радиоимпульса с известной амплитудой и случайной начальной фазой, имеющей равномерное распределение в интервале
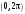.Физический смысл некогерентного приема методом однократного отсчета сводится к следующему: поскольку начальная фаза несущего колебания неизвестна (случайна), теперь нельзя выбрать момент 
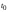измерения мгновенного значения так, чтобы значение сигнала 
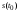было максимальным. Поэтому сначала выполняется выделение огибающей наблюдаемого процесса, а затем берется ее отсчет 
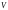в любой момент в пределах длительности посылки. Выбор порога 
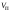для принятия решения на основе однократного отсчета огибающей производится аналогично когерентному случаю с той разницей, что теперь мгновенное значение имеет негауссово распределение при обеих гипотезах. Если сигнала нет (при гипотезе 
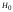), наблюдаемый процесс представляет собой гауссовский шум с нулевым средним, а его огибающая 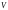в произвольный момент времени имеет распределение Рэлея 
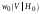. Если сигнал присутствует (при гипотезе 
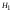), огибающая гауссовского процесса имеет распределение Рэлея–Райса (обобщенное рэлеевское) 
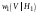, что соответствует ненулевому среднему. Аналогично когерентному приему производится учет априорных вероятностей гипотез путем домножения соответствующих условных плотностей распределения на коэффициенты равные этим априорным вероятностям.
Условные плотности распределения проверяемых приемником гипотез имеют вид:
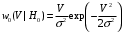для гипотезы 
- «сигнала нет»;
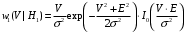для гипотезы 
- «сигнала есть»;
г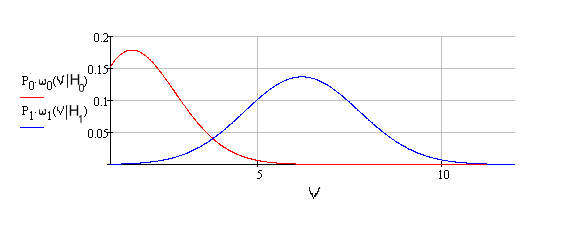
де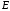 
- энергия сигнала,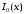 
г) отнести результат к средней длине кодового слова.
Таким образом:
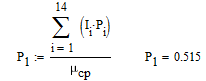
Энтропия кода находится как энтропия случайной величины, принимающей два значения (0 и 1) с вероятностям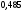и
и 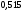: Избыточность кода:
где
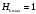- максимальная энтропия двоичного кода.Скорость передачи информации
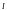по каналу без помех определяется только временем передачи одного кодового символа (равным длительности посылки ), средней длиной кодового слова 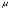и средним количеством информации, заключенной в кодовом слове, равным энтропии 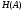исходного источника. Нетрудно видеть, что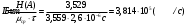 6. Описание процесса принятия решения при приеме сигнала
В данной курсовой работе рассматривается задача построения оптимального демодулятора (приемника) для случая амплитудной телеграфии с пассивной паузой, что соответствует принятию решения о том, что передавался символ 0 (сигнала нет) или символ 1 (сигнал есть). Таким образом, решается задача обнаружения сигнала в наблюдаемом колебании. В работе предполагается, что помеха в канале представляет собой гауссовский шум с нулевым средним и известной дисперсией, который взаимодействует с сигналом аддитивно (суммируется). Результатом обработки наблюдаемого колебания является случайная величина
y , которая может иметь различное распределение в зависимости от того, есть ли сигнал в наблюдаемом колебании, а именно: распределение при гипотезе H0 – «сигнала нет» – является гауссовским с нулевым средним, а распределение при гипотезе H1 – «сигнал есть» – отличается сдвигом на величину a, зависящую от способа обработки (в данном случае амплитуда несущего колебания). Значение a предполагается известным. Таким образом, проверяемые гипотезы описываются двумя условнымиплотностями распределения вероятностей w(y |H0) и w(y | H1).
В данной постановке демодулятор (приемник) может принимать решение, основываясь только на наблюдаемом значении
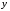: очевидно, чем больше наблюдаемое значение, тем с большей уверенностью можно утверждать, что сигнал в принятом колебании есть. Приемник в таком случае должен сравнить 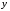с некоторым фиксированным значением (порогом) 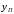и если 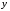больше порога, принять решение о наличии сигнала, в противном случае – о его отсутствии, что можно кратко записать в следующей символической форме:
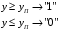
7. Расчет характеристик согласно пункту 2.3
Когерентный прием
Когерентным приемом или приемом полностью известного сигнала называется принятие решения в системе связи при следующих условиях: синхронизация является точной и форма сигнала на интервале наблюдения точно известна, неизвестен лишь сам факт наличия либо отсутствия сигнала в наблюдаемом колебании. (Эта ситуация наиболее близка к реальности в кабельных линиях связи, где условия распространения сигналов известны и практически неизменны.)
Как было сказано в пункте 6, принимаемое демодулятором решение основывается на сравнении значения наблюдаемой реализации с некоторым фиксированным (пороговым) значением
. Условные плотности распределения проверяемых приемником гипотез имеют вид:
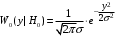для гипотезы 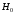- «сигнала нет»; 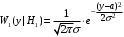для гипотезы 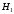- «сигнала есть»;где
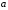- амплитуда сигнала и 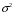- дисперсия шума даны. Каким бы ни был порог
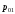, очевидно, есть некоторая ненулевая вероятность принять решение о наличии сигнала при его фактическом отсутствии. Эта вероятность называется условной вероятностью ошибки первого рода («ложной тревоги») и определяется выражением: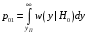 Аналогично, существует ненулевая вероятность принять решение об отсутствии сигнала, в то время как на самом деле он есть (условная вероятность ошибки второго рода, или пропуска сигнала):
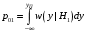
Очевидно, сумма указанных условных вероятностей минимальна, если порог
находится как абсцисса точки пересечения условных плотносте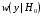й:
и 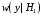При таком выборе порога приемник является оптимальным по критерию минимума суммарной условной вероятности ошибки. В нашем случае, априорные вероятности проверяемых гипотез различны, поэтому мы переходим к критерию идеального наблюдателя (к построению оптимального байесовского приемника, обеспечивающего минимальную среднюю вероятность ошибки). В этом случае оптимальный порог
выбирается из условия: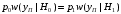 где
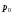и 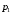- априорные вероятности гипотез. Рис.5. Условные плотности распределения гипотез, умноженные на априорные вероятности двоичных символов, при когерентном приеме
Используя математический пакет MathCAD определим оптимальный порог
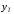
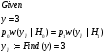
Таким образом,
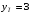.Значит, условная вероятность ошибки первого рода равна:
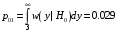
Условная вероятность ошибки второго рода равна:
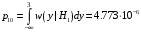
Средняя вероятность ошибки:
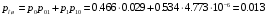
Некогерентный прием
Случай точно известного сигнала на практике является скорее исключением. Обычно некоторые параметры сигнала на приемной стороне канала связи неизвестны. В курсовой работе рассматривается прием сигнала, имеющего форму прямоугольного радиоимпульса с известной амплитудой и случайной начальной фазой, имеющей равномерное распределение в интервале
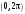.Физический смысл некогерентного приема методом однократного отсчета сводится к следующему: поскольку начальная фаза несущего колебания неизвестна (случайна), теперь нельзя выбрать момент 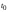измерения мгновенного значения так, чтобы значение сигнала 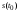было максимальным. Поэтому сначала выполняется выделение огибающей наблюдаемого процесса, а затем берется ее отсчет 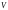в любой момент в пределах длительности посылки. Выбор порога 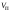для принятия решения на основе однократного отсчета огибающей производится аналогично когерентному случаю с той разницей, что теперь мгновенное значение имеет негауссово распределение при обеих гипотезах. Если сигнала нет (при гипотезе 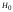), наблюдаемый процесс представляет собой гауссовский шум с нулевым средним, а его огибающая 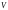в произвольный момент времени имеет распределение Рэлея 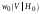. Если сигнал присутствует (при гипотезе 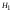), огибающая гауссовского процесса имеет распределение Рэлея–Райса (обобщенное рэлеевское) 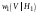, что соответствует ненулевому среднему. Аналогично когерентному приему производится учет априорных вероятностей гипотез путем домножения соответствующих условных плотностей распределения на коэффициенты равные этим априорным вероятностям.Условные плотности распределения проверяемых приемником гипотез имеют вид:
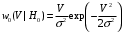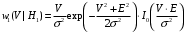для гипотезы - «сигнала нет»; для гипотезы - «сигнала есть»;г
де 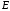- энергия сигнала,