Файл: 3. Метод наименьших квадратов и специальные интерполяционные многочлены.doc
Добавлен: 30.11.2023
Просмотров: 79
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Метод наименьших квадратов и специальные интерполяционные многочлены
3.1. Постановка задачи и вывод формул метода наименьших квадратов
3.2. Лабораторная работа № 4. Аппроксимация функции по методу наименьших квадратов
3.3. Глобальная полиномиальная интерполяция
3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
. Это нули многочлена 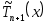 . При таком выборе
. При таком выборе
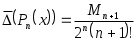 , (3.6.2)
, (3.6.2)
причем любой другой выбор узлов дает большее значение верхней границы погрешности. Для формулы Тейлора, например,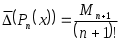 , то есть в
, то есть в 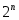 раз хуже.
раз хуже.
Перейдем теперь к отрезку . Его можно преобразовать к стандартному отрезку
. Его можно преобразовать к стандартному отрезку  следующей заменой:
следующей заменой: 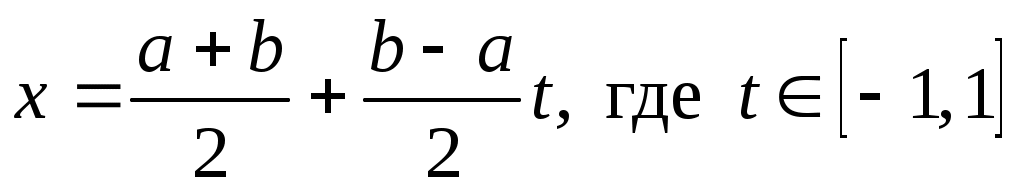 . В этом случае
. В этом случае
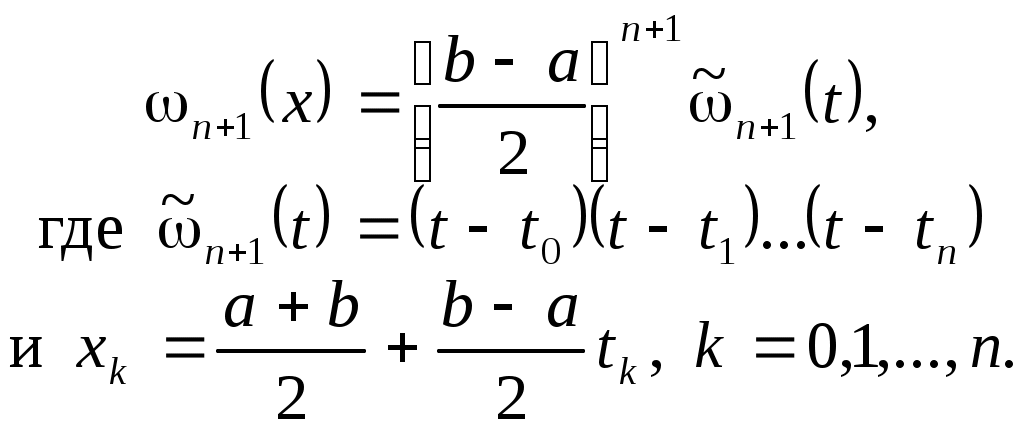 (3.6.3)
(3.6.3)
Тогда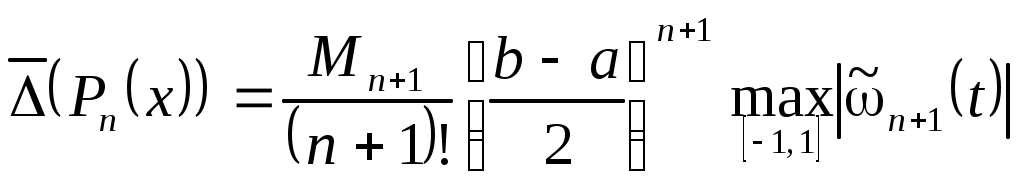 (3.6.4)
(3.6.4)
и минимум этой величины достигается при значениях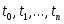 , совпадающих с нулями многочлена
, совпадающих с нулями многочлена 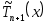 . Таким образом, решение поставленной задачи дает выбор узлов
. Таким образом, решение поставленной задачи дает выбор узлов
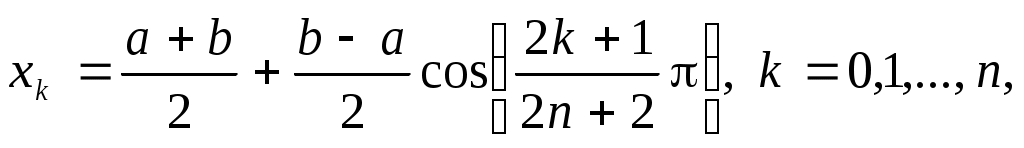 (3.6.5)
(3.6.5)
и ему соответствует минимальное значение верхней границы погрешности интерполяции, равное: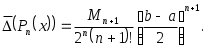 (3.6.6)
(3.6.6)
Функциональный ряд вида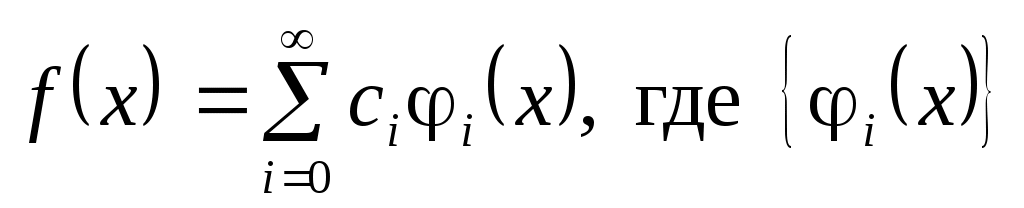 - система базисных функций, называется рядом Фурье функции
- система базисных функций, называется рядом Фурье функции  на отрезке
на отрезке  по системе функций
по системе функций 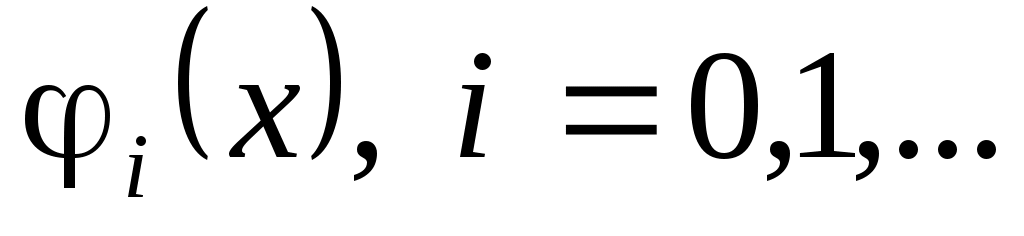 с весом
с весом  на
на  , если коэффициенты
, если коэффициенты 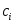 вычисляются по формулам вида
вычисляются по формулам вида 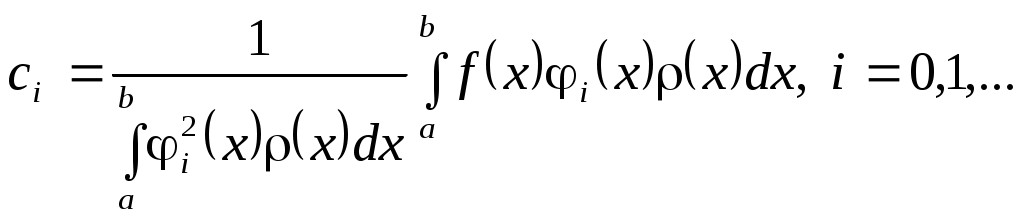 (3.7.1)
(3.7.1)
Так как для полиномов Чебышева весовая функция равна: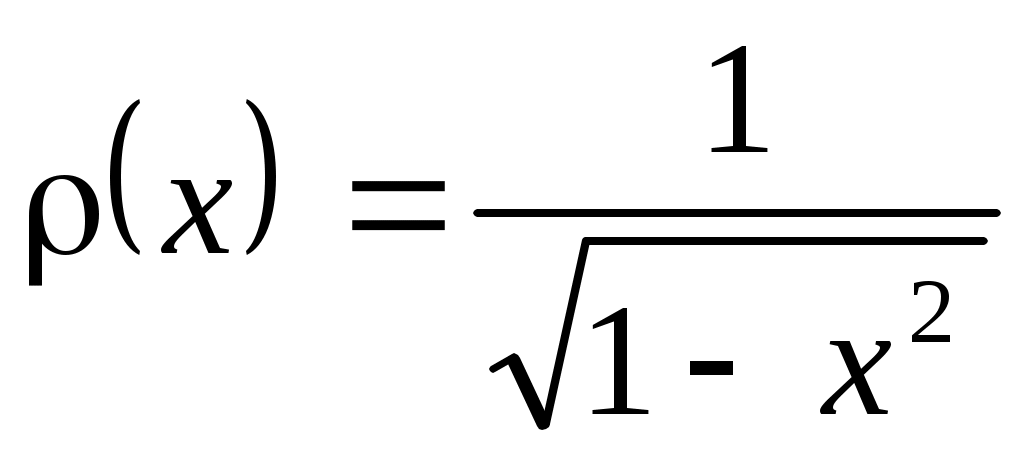 на
на 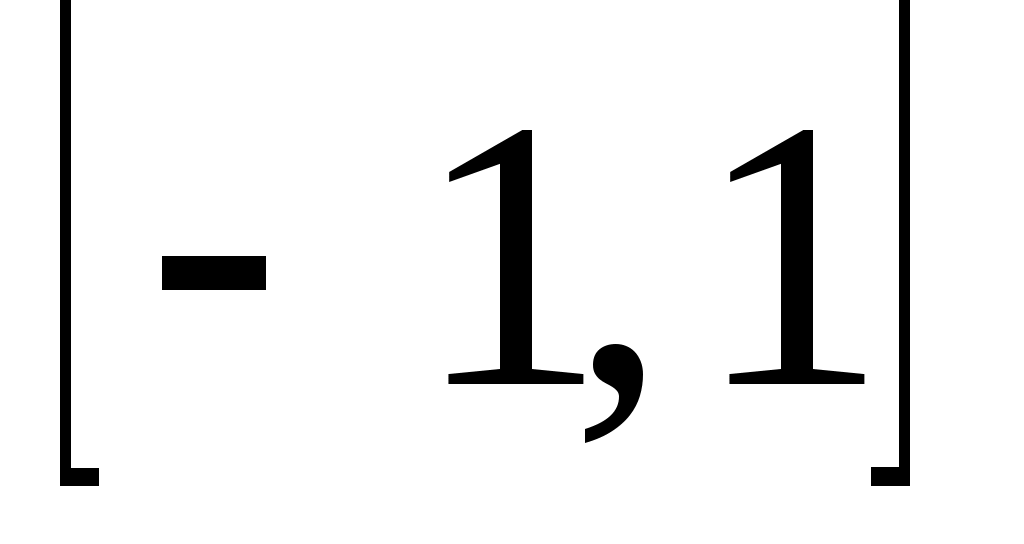 ,
,
то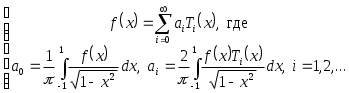 (3.7.2)
(3.7.2)
Пример. Разложить в ряд Фурье по полиномам Чебышева функцию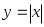 на отрезке
на отрезке  .
.
Функция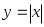 - четная, поэтому, как во всяком ряду Фурье, нечетные коэффициенты будут равны нулю, четные же можно сдвоить, уменьшив при этом интервал интегрирования вдвое. Тогда
- четная, поэтому, как во всяком ряду Фурье, нечетные коэффициенты будут равны нулю, четные же можно сдвоить, уменьшив при этом интервал интегрирования вдвое. Тогда 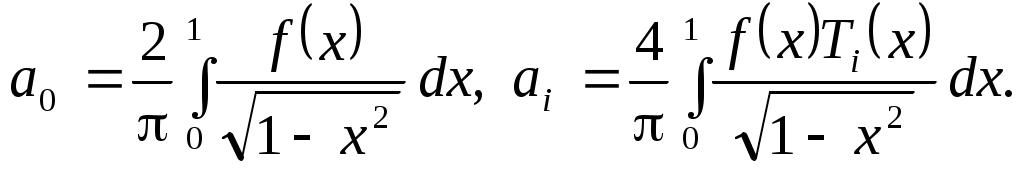 Вычислим коэффициенты разложения:
Вычислим коэффициенты разложения:
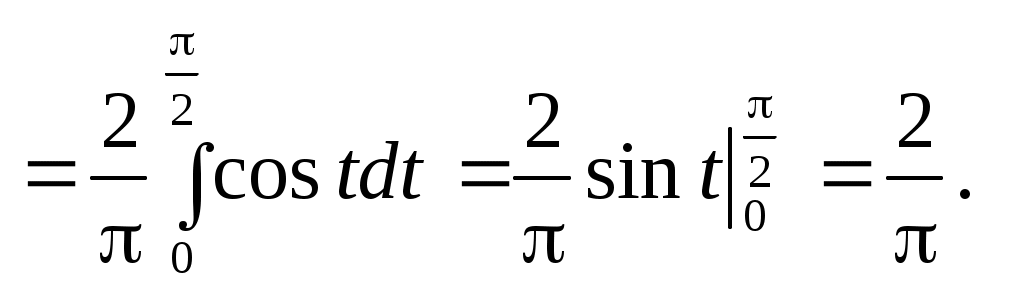
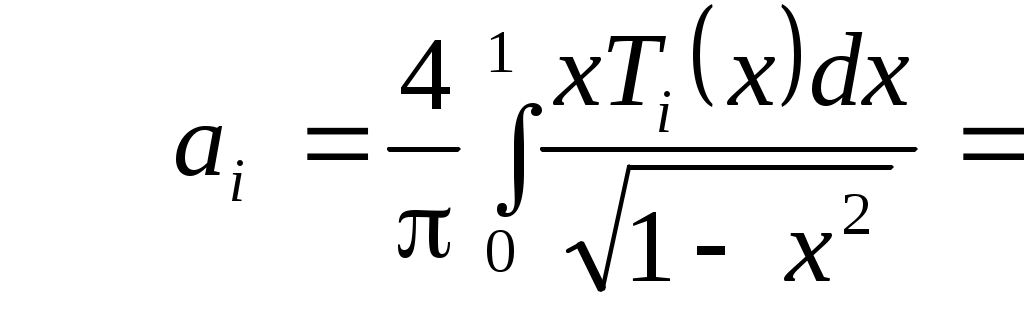
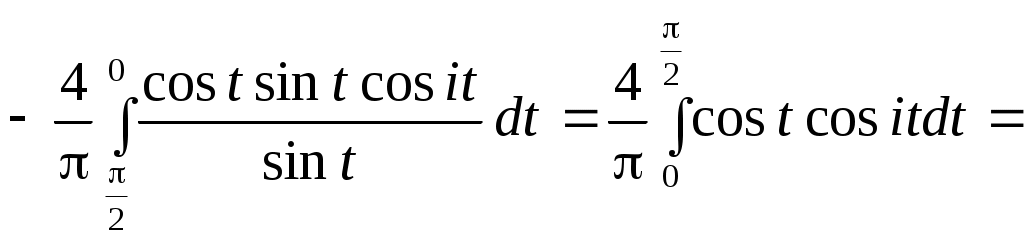
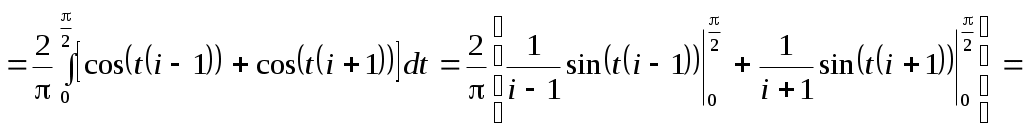
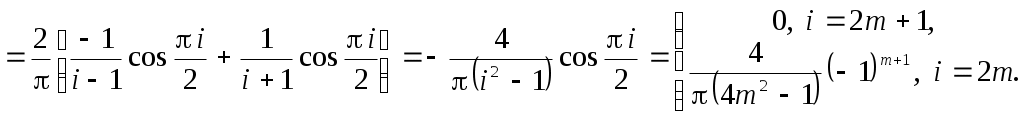
Итак,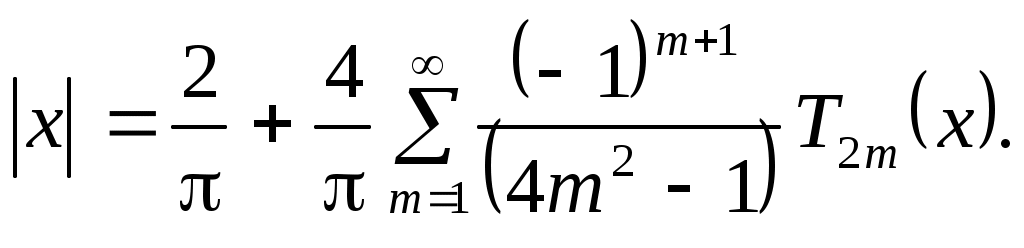
Пример. По равномерной (а) и специальной (б) таблице значений функции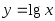 найти
найти  и оценить погрешность. Использовать формулы Ньютона с разделенными разностями.
и оценить погрешность. Использовать формулы Ньютона с разделенными разностями.
(а)
(б)
Так как таблицы короткие, то по ним можно вычислить разделенные разности лишь до четвертого порядка. Точки аргумента в таблице (б) - это нули многочлена Чебышева пятой степени, то есть точки, где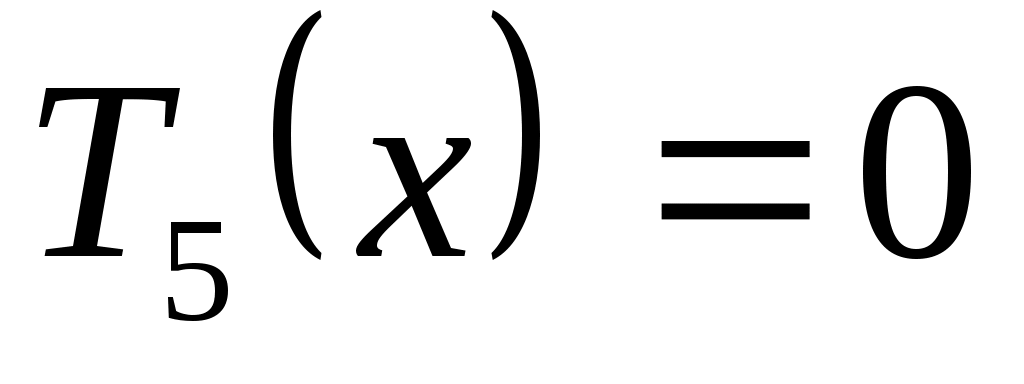 , приведенные к отрезку
, приведенные к отрезку 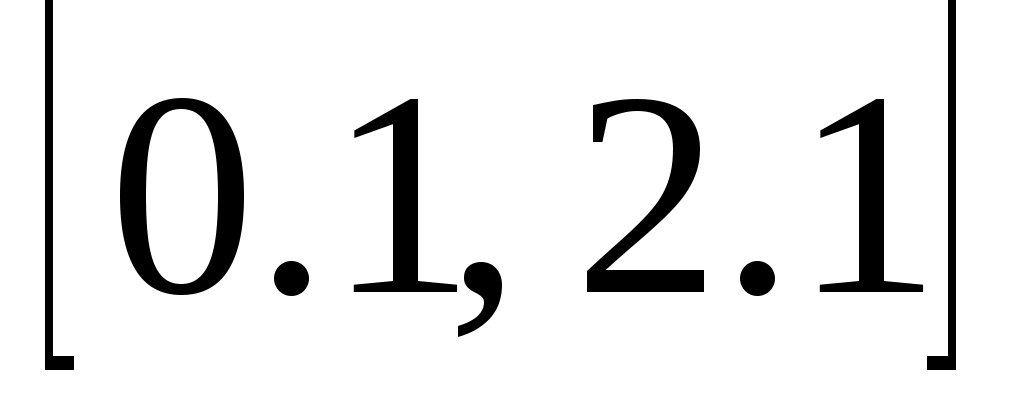 по формуле
по формуле
 1
1
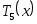







0.1 1.1 2.1 -1 1
-1 -1
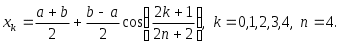 Действительно,
Действительно, 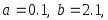
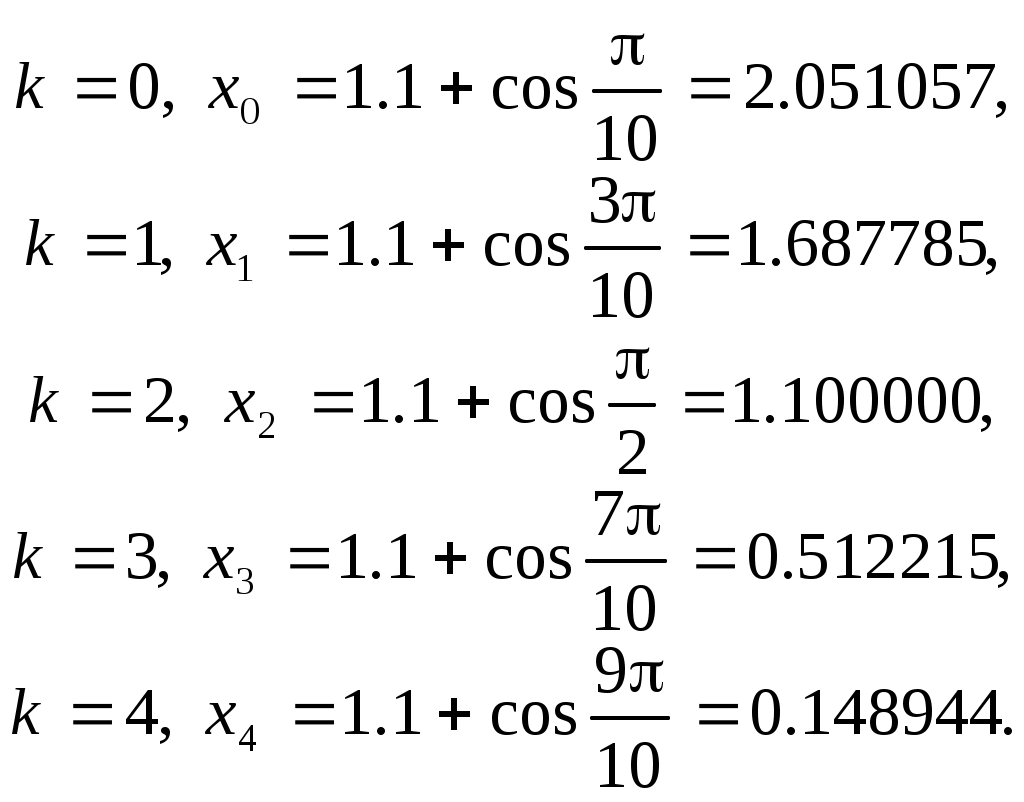
Согласно теории, в случае расположения узлов интерполяции в нулях многочлена
Чебышева гарантирована минимальная погрешность интерполяции, равная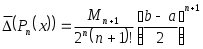 , в отличие от обычной интерполяции по формуле Ньютона с разделенными разностями, где погрешность равна:
, в отличие от обычной интерполяции по формуле Ньютона с разделенными разностями, где погрешность равна: 
Построим для случаев (а) и (б) таблицы разделенных разностей.
(а)
(б)
причем любой другой выбор узлов дает большее значение верхней границы погрешности. Для формулы Тейлора, например,
Перейдем теперь к отрезку
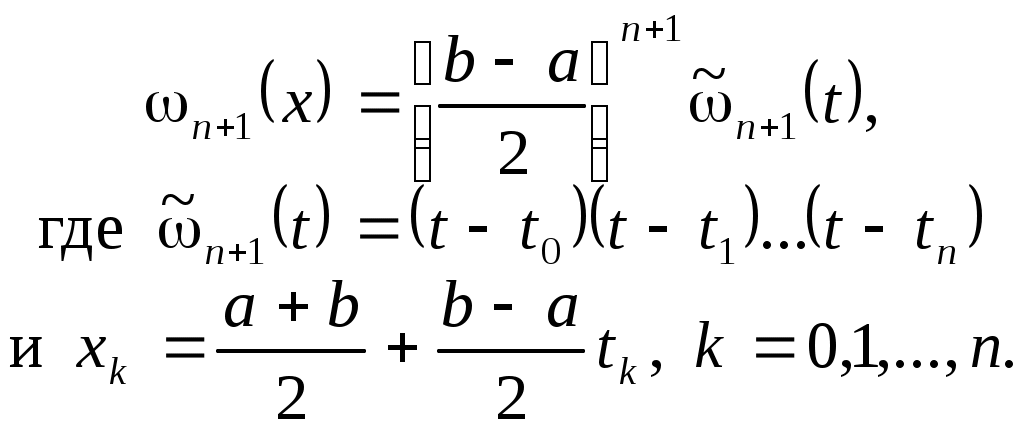 (3.6.3)
(3.6.3)Тогда
и минимум этой величины достигается при значениях
и ему соответствует минимальное значение верхней границы погрешности интерполяции, равное:
3.7. Ряд Фурье1 по многочленам Чебышева
Функциональный ряд вида
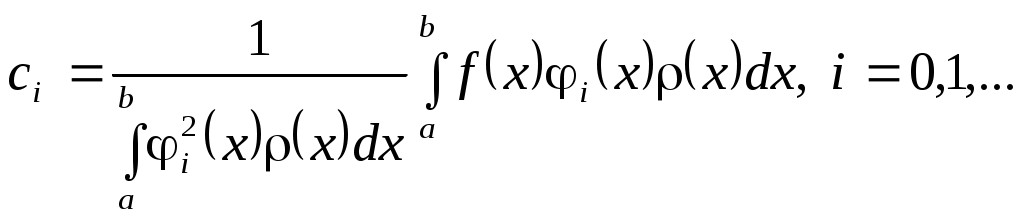 (3.7.1)
(3.7.1)Так как для полиномов Чебышева весовая функция равна:
то
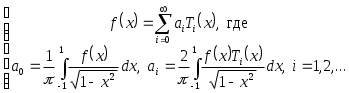 (3.7.2)
(3.7.2)Пример. Разложить в ряд Фурье по полиномам Чебышева функцию
Функция
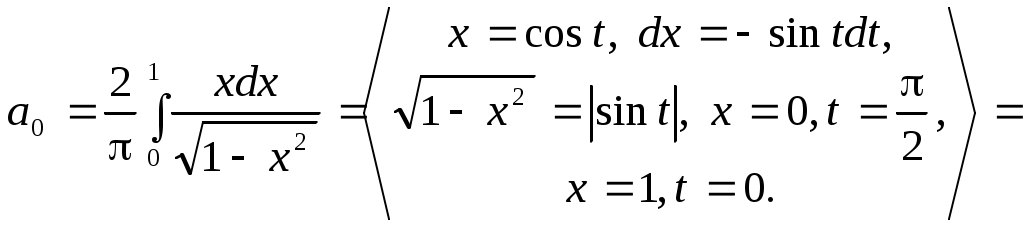

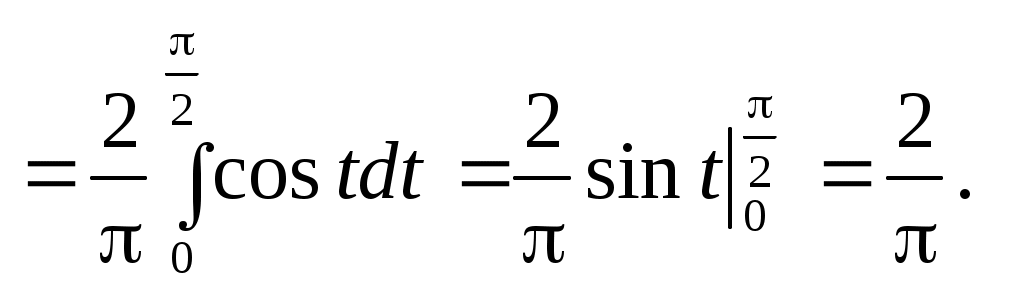
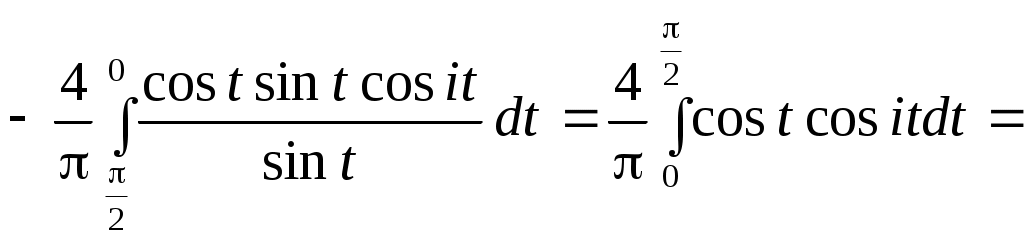
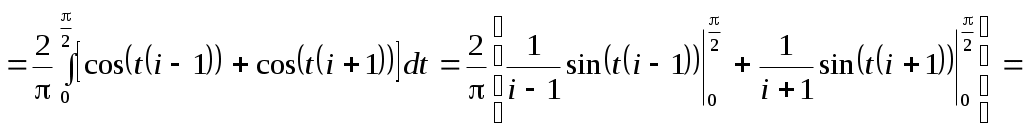
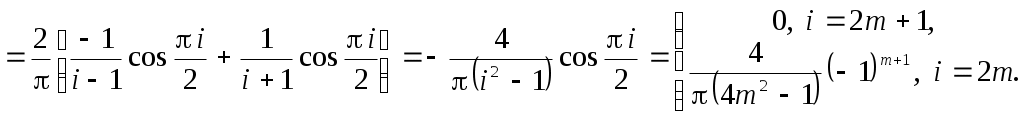
Итак,
Пример. По равномерной (а) и специальной (б) таблице значений функции
(а)
-

0.1
0.6
1.1
1.6
2.1

-1.000000
-0.221849
0.041393
0.204120
0.322219
(б)
-

0.148944
0.512215
1.1
1.687785
2.051057

-0.826977
-0.290548
0.041393
0.227317
0.311978
Так как таблицы короткие, то по ним можно вычислить разделенные разности лишь до четвертого порядка. Точки аргумента в таблице (б) - это нули многочлена Чебышева пятой степени, то есть точки, где
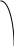
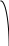
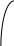 1
1 


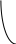



0.1 1.1 2.1 -1 1
-1 -1
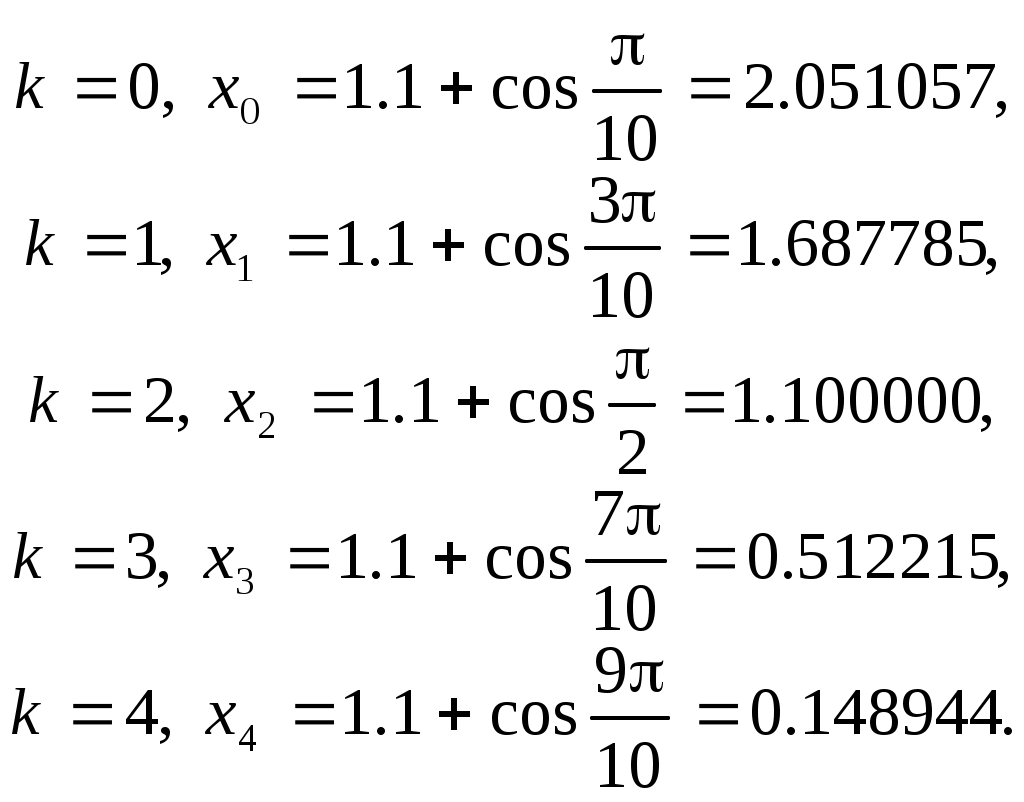
Согласно теории, в случае расположения узлов интерполяции в нулях многочлена
Чебышева гарантирована минимальная погрешность интерполяции, равная
Построим для случаев (а) и (б) таблицы разделенных разностей.
(а)
-


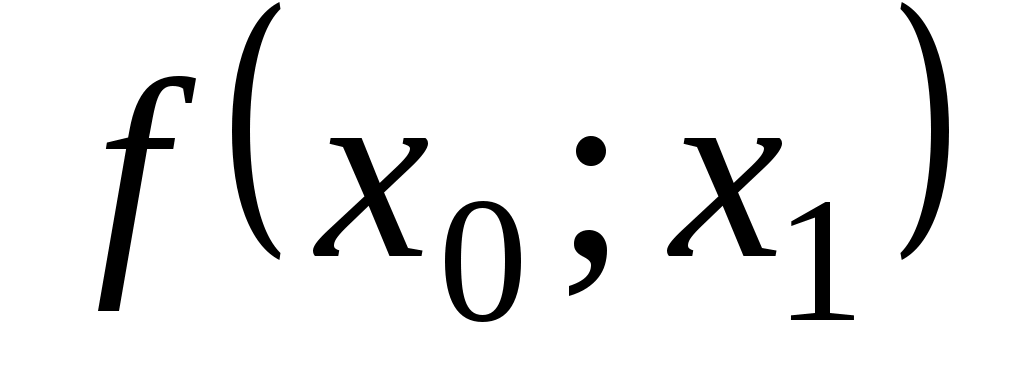
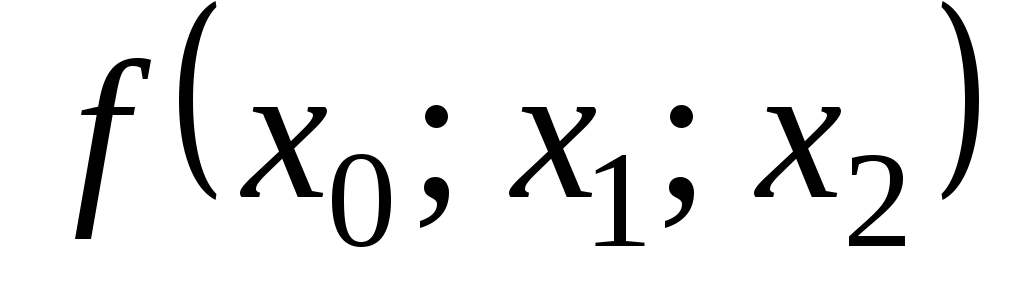
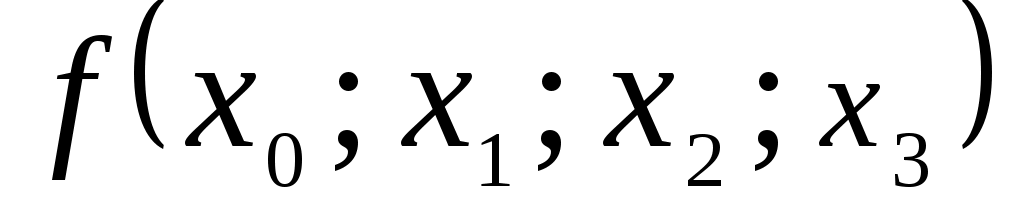
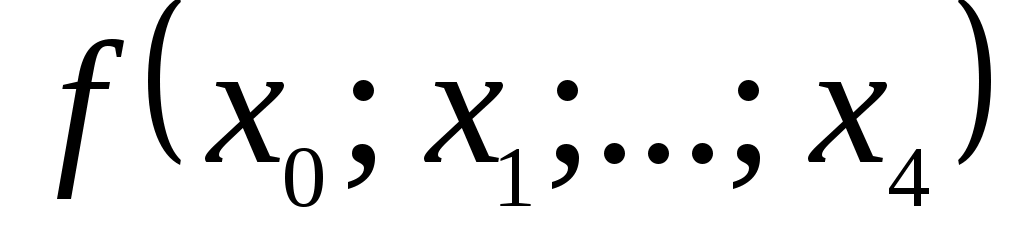
0
0.1
-1.000000
1.556302
1
0.6
-0.221849
-1.029818
0.526484
0.552525
2
1.1
0.041393
-0.201030
-0.239005
0.325454
0.074516
3
1.6
0.204120
-0.089256
0.236198
4
2.1
0.322219
(б)
| | | | | | | |
| 0 | 0.148944 | -0.826977 | | | | |
| | | | 1.476663 | | | |
| 1 | 0.512215 | -0.290548 | | -0.958862 | | |
| | | | 0.564732 | | 0.485784 | |
| 2 | 1.100000 | 0.041393 | | -0.211318 | | -0.213107 |
| | | | 0.316313 | | 0.080431 | |
| 3 | 1.687785 | 0.227317 | | -0.087547 | | |
| | | | 0.233051 | | | |
| 4 | 2.051057 | 0.311978 | | | | |