Файл: 3. Метод наименьших квадратов и специальные интерполяционные многочлены.doc
Добавлен: 30.11.2023
Просмотров: 85
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Метод наименьших квадратов и специальные интерполяционные многочлены
3.1. Постановка задачи и вывод формул метода наименьших квадратов
3.2. Лабораторная работа № 4. Аппроксимация функции по методу наименьших квадратов
3.3. Глобальная полиномиальная интерполяция
3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
Вычисления по этим таблицам дают:
(а)
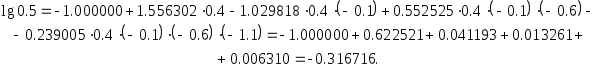
(б)
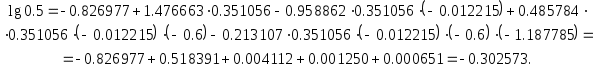
Истинное значение
таким образом, предельная погрешность в случае (а) достигает 
а в случае (б) 
то есть на порядок меньше.Так как таблица разностей очень короткая, а
вблизи точки 
меняется быстро (см. график функции ), то попытка оценить погрешность по известным формулам не даст достоверного результата, то есть погрешность будет слишком завышена. Действительно, 
Так же, огрубляя оценку и вспоминая график
0.1 2.1 0.1 0.6 1.1 1.6 2.1
функции
, будем иметь 
где 
Тогда 
Аналогично для случая (б) 
Оба результата не реальны.1 Иорген Педерсен Грам (1850-1916 ) - датский математик.
Карл Вейерштрасс (1815-1897) – немецкий математик.
Карл Давид Тольме Рунге (1856-1927) - немецкий физик и математик.
Жорж Фабер (1877-1966) - швейцарский математик.
Пафнутий Львович Чебышев (1821-1894) – русский математик и механик.
Анри Леон Лебег (1875-1941) - французский математик.
1 Родриг; Бенжамен Оленд Родригес (1794-1851) - французский математик и экономист.
1 Жан Батист Жозеф Фурье (1768-1830) - французский математик.