Файл: 3. Метод наименьших квадратов и специальные интерполяционные многочлены.doc
Добавлен: 30.11.2023
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Метод наименьших квадратов и специальные интерполяционные многочлены
3.1. Постановка задачи и вывод формул метода наименьших квадратов
3.2. Лабораторная работа № 4. Аппроксимация функции по методу наименьших квадратов
3.3. Глобальная полиномиальная интерполяция
3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
(3.5.3)
2. Являются решениями следующего дифференциального уравнения:
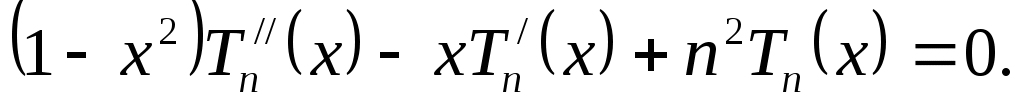 (3.5.4)
(3.5.4)
3. Определяются из формулы Родрига1
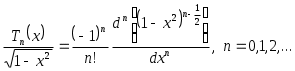 (3.5.5)
(3.5.5)
4. Определяются рекуррентно:
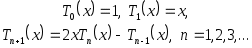 (3.5.6)
(3.5.6)
Иногда в качестве полиномов Чебышева берут функции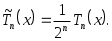
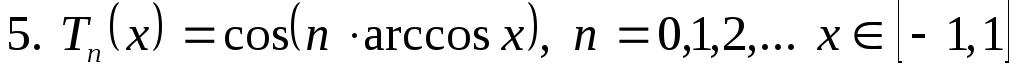 . (3.5.7)
. (3.5.7)
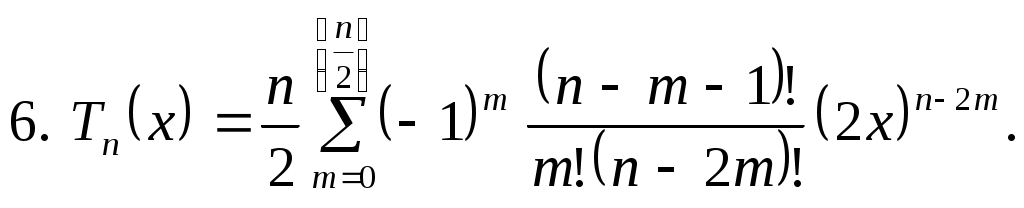 (3.5.8)
(3.5.8)
Многочлены Чебышева обладают множеством замечательных свойств.
Теорема 3.4. Полиномы Чебышева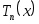 образуют на отрезке
образуют на отрезке  ортогональную систему с весом
ортогональную систему с весом 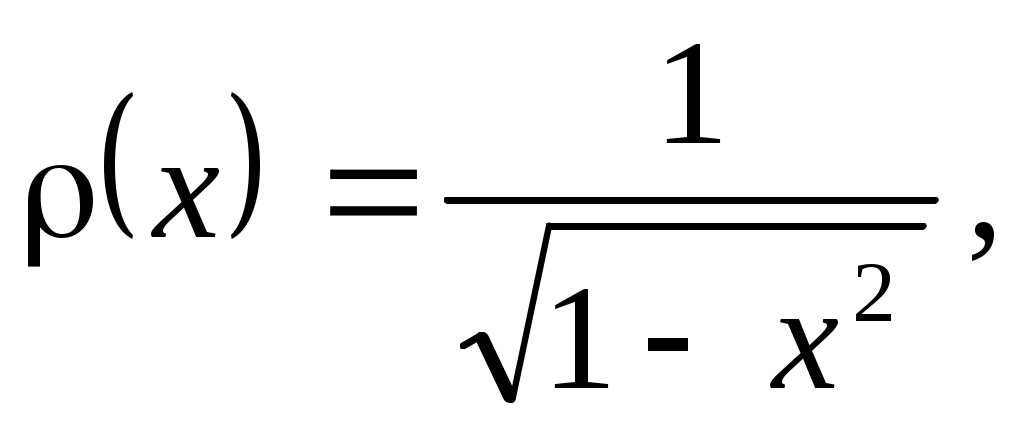 то есть
то есть
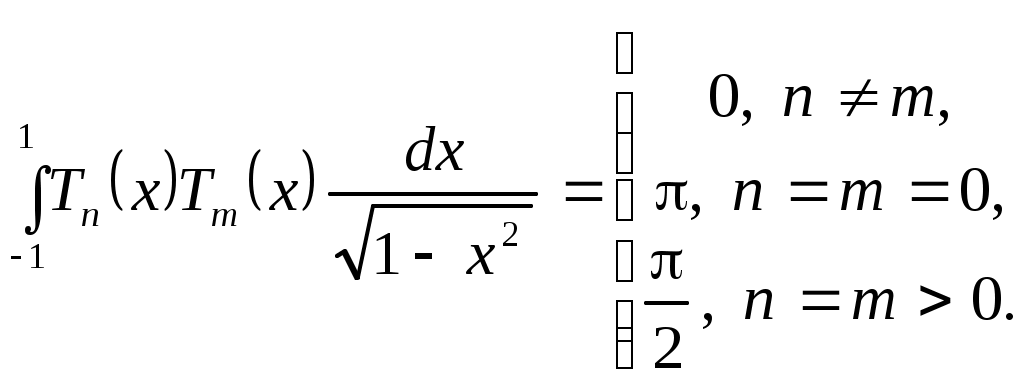 (3.5.9)
(3.5.9)
Действительно,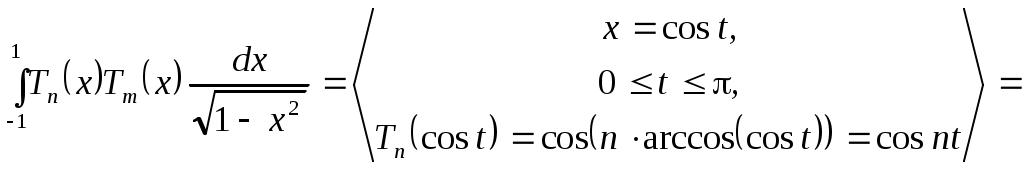
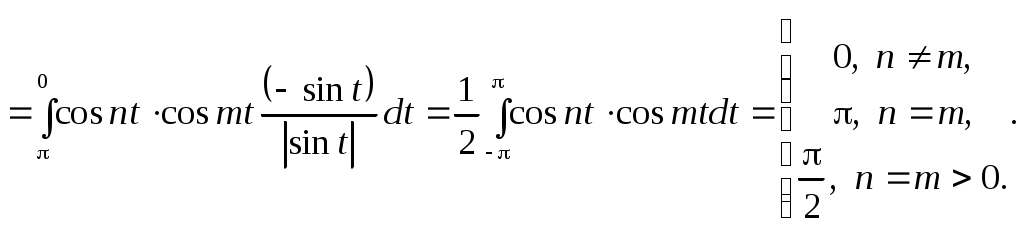

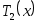
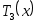
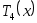
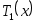
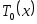
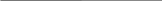


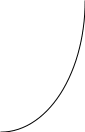
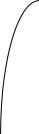
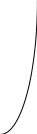

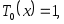
1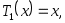
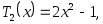
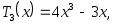
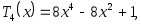


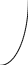
 -1 1
-1 1 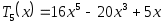
и так далее.
-1
Теорема 3.5. При четном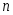 многочлен
многочлен  содержит только четные степени
содержит только четные степени  и является четной функцией, а при нечетном
и является четной функцией, а при нечетном 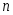 многочлен
многочлен  содержит только нечетные степени
содержит только нечетные степени  и является нечетной функцией.
и является нечетной функцией.
Теорема 3.6. При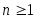 старший коэффициент многочлена
старший коэффициент многочлена  равен
равен 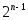 , то есть
, то есть 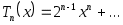
Теорема 3.7. При многочлен
многочлен  имеет ровно
имеет ровно  действительных корней, расположенных на отрезке
действительных корней, расположенных на отрезке  и вычисляемых по формуле
и вычисляемых по формуле
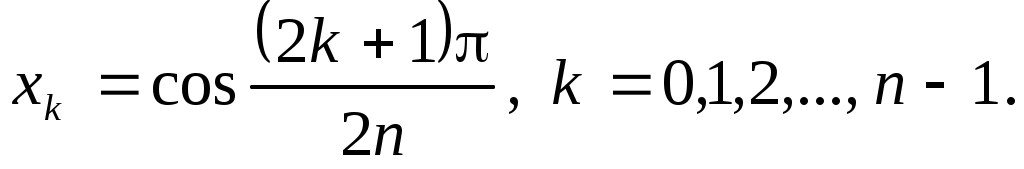 (3.5.10)
(3.5.10)
Теорема 3.8. При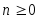 справедливо равенство
справедливо равенство 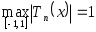 . Если
. Если  , то этот максимум достигается ровно в
, то этот максимум достигается ровно в 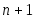 точках, которые находятся по формуле
точках, которые находятся по формуле
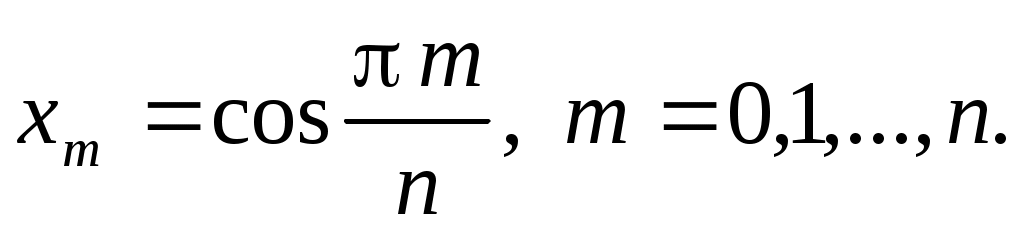 (3.5.11)
(3.5.11)
При этом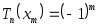 , то есть максимумы и минимумы многочлена Чебышева чередуются.
, то есть максимумы и минимумы многочлена Чебышева чередуются.
Теоремы 3.7 и 3.8 легко доказываются с помощью формулы (3.5.7).
Назовем величину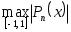 уклонением многочлена
уклонением многочлена  от нуля. Тогда справедлива следующая, доказанная П.Л. Чебышевым в 1854 г. теорема.
от нуля. Тогда справедлива следующая, доказанная П.Л. Чебышевым в 1854 г. теорема.
Теорема 3.9. Среди всех многочленов фиксированной степени со старшим коэффициентом
со старшим коэффициентом 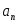 , равным единице, наименьшее уклонение от нуля, равное
, равным единице, наименьшее уклонение от нуля, равное 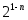 , имеет многочлен
, имеет многочлен 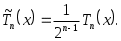
Последнее свойство имеет особую ценность для приложений. Действительно, тогда для любого многочлена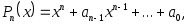 отличного от
отличного от 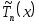
, справедливо неравенство
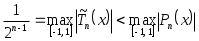 . (3.5.12)
. (3.5.12)
В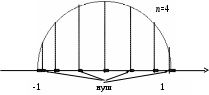 силу формул (3.5.10) и (3.5.11) нули и точки экстремума полинома
силу формул (3.5.10) и (3.5.11) нули и точки экстремума полинома  можно построить следующим образом: разделив полуокружность, опирающуюся на отрезок
можно построить следующим образом: разделив полуокружность, опирающуюся на отрезок  на
на 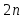 частей, спроецируем полученные точки на диаметр. Нумеруя проекции слева направо, получим, что все проекции с нечетными номерами являются нулями полинома
частей, спроецируем полученные точки на диаметр. Нумеруя проекции слева направо, получим, что все проекции с нечетными номерами являются нулями полинома  , а с четными – его точками экстремума. Из геометрических соображений вытекает, что как нули, так и точки экстремума полинома
, а с четными – его точками экстремума. Из геометрических соображений вытекает, что как нули, так и точки экстремума полинома  сгущаются к концам отрезка
сгущаются к концам отрезка  .
.
Предположим, что значение заданной на отрезке функции
функции 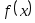 можно вычислить в произвольной точке
можно вычислить в произвольной точке  . Однако по некоторым причинам целесообразнее заменить прямое вычисление функции
. Однако по некоторым причинам целесообразнее заменить прямое вычисление функции 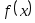 вычислением значений ее интерполяционного многочлена. Для такой замены необходимо один раз получить таблицу значений
вычислением значений ее интерполяционного многочлена. Для такой замены необходимо один раз получить таблицу значений 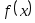 в выбранных точках
в выбранных точках 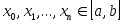 . При этом естественно стремиться к такому выбору узлов интерполяции, который позволит сделать минимальной величину
. При этом естественно стремиться к такому выбору узлов интерполяции, который позволит сделать минимальной величину 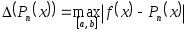 .
.
Пусть о функции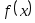 известно лишь то, что она непрерывно дифференцируема
известно лишь то, что она непрерывно дифференцируема  раз на отрезке
раз на отрезке  . Тогда
. Тогда
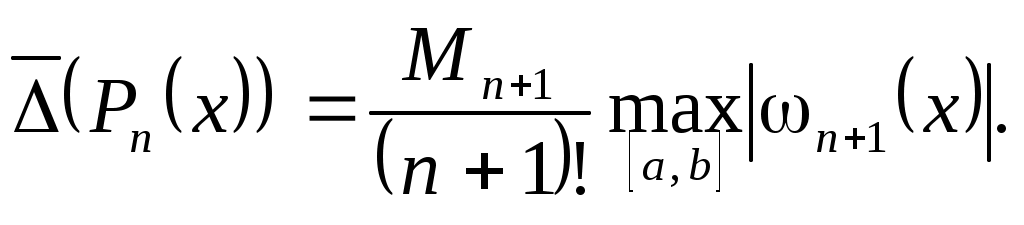 (3.6.1)
(3.6.1)
Найдем теперь набор узлов интерполяции , при котором
, при котором 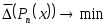 . Пусть сначала
. Пусть сначала 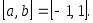 В этом случае величина (3.6.1) будет минимальна, если будет минимальна
В этом случае величина (3.6.1) будет минимальна, если будет минимальна 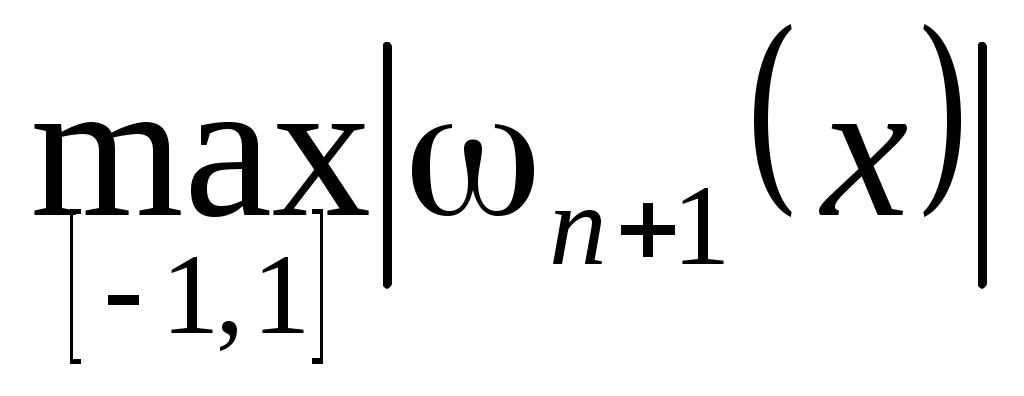 . Но этим свойством обладают полиномы Чебышева, следовательно,
. Но этим свойством обладают полиномы Чебышева, следовательно, 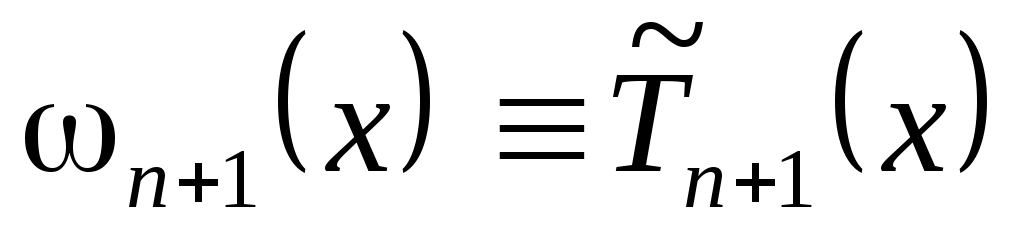 , и набор узлов определен
, и набор узлов определен 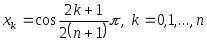
2. Являются решениями следующего дифференциального уравнения:
3. Определяются из формулы Родрига1
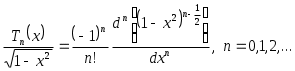 (3.5.5)
(3.5.5)4. Определяются рекуррентно:
Иногда в качестве полиномов Чебышева берут функции
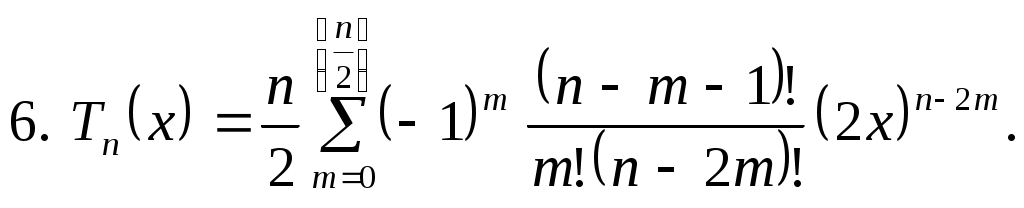 (3.5.8)
(3.5.8)Многочлены Чебышева обладают множеством замечательных свойств.
Теорема 3.4. Полиномы Чебышева
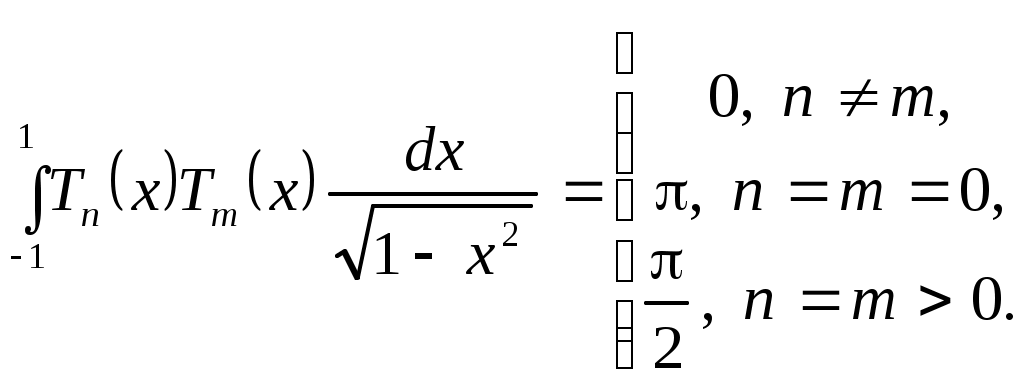 (3.5.9)
(3.5.9)Действительно,
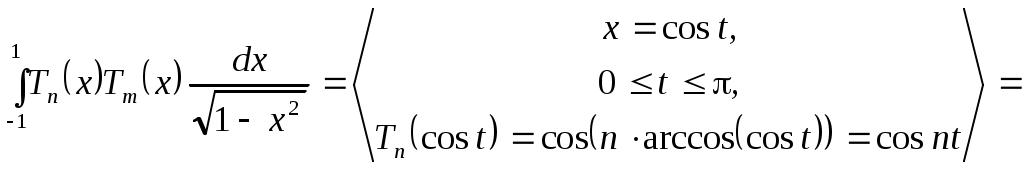
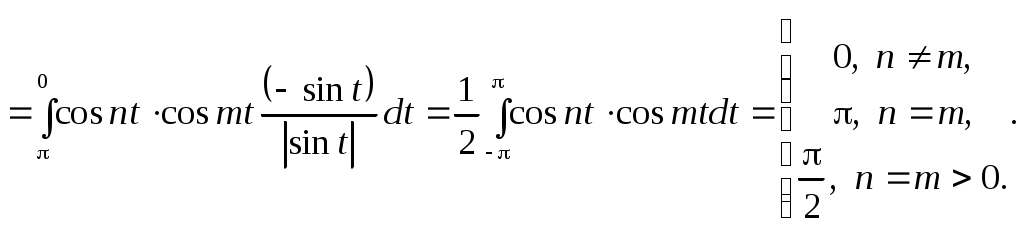




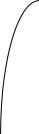
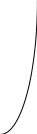

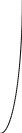
1


 -1 1
-1 1 и так далее.
-1
Теорема 3.5. При четном
Теорема 3.6. При
Теорема 3.7. При
Теорема 3.8. При
При этом
Теоремы 3.7 и 3.8 легко доказываются с помощью формулы (3.5.7).
Назовем величину
Теорема 3.9. Среди всех многочленов фиксированной степени
Последнее свойство имеет особую ценность для приложений. Действительно, тогда для любого многочлена
, справедливо неравенство
В
 силу формул (3.5.10) и (3.5.11) нули и точки экстремума полинома
силу формул (3.5.10) и (3.5.11) нули и точки экстремума полинома 3.6. Решение задачи минимизации оценки погрешности
Предположим, что значение заданной на отрезке
Пусть о функции
Найдем теперь набор узлов интерполяции