Файл: 3. Метод наименьших квадратов и специальные интерполяционные многочлены.doc
Добавлен: 30.11.2023
Просмотров: 82
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Метод наименьших квадратов и специальные интерполяционные многочлены
3.1. Постановка задачи и вывод формул метода наименьших квадратов
3.2. Лабораторная работа № 4. Аппроксимация функции по методу наименьших квадратов
3.3. Глобальная полиномиальная интерполяция
3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
Используя метод наименьших квадратов, аппроксимируем ее многочленами первой и второй степени и найдем соответствующие средние квадратические уклонения
Вычисления, которые нужно провести, расположим по схеме, приведенной в такой таблице:
-
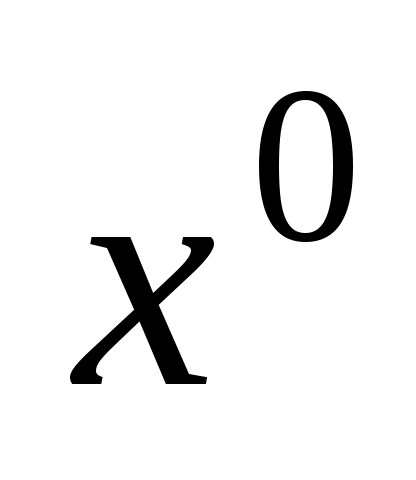
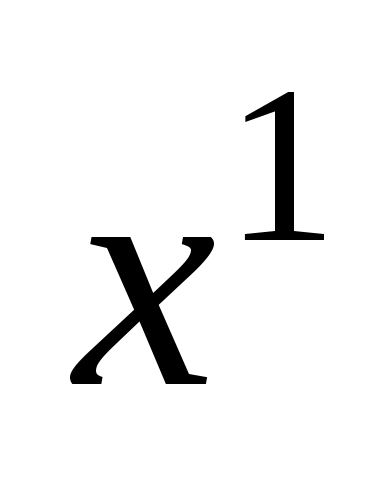
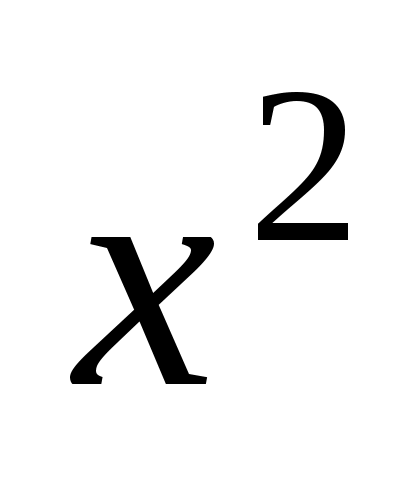
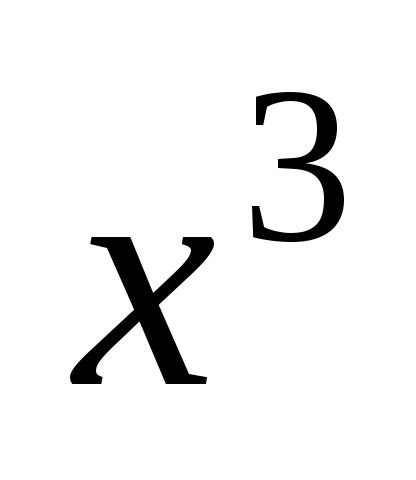
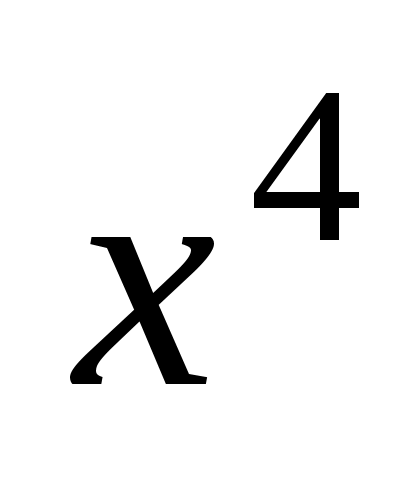
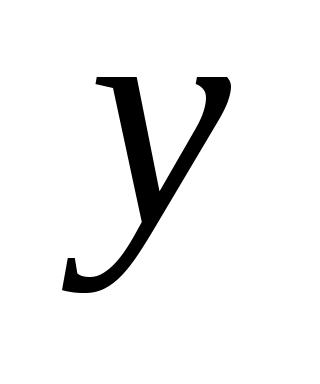
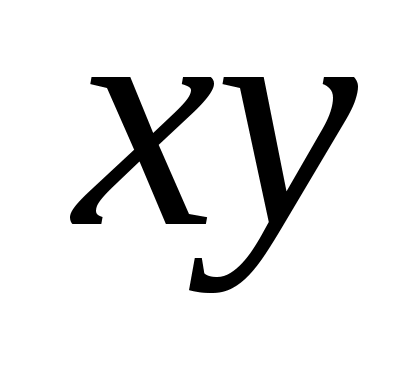
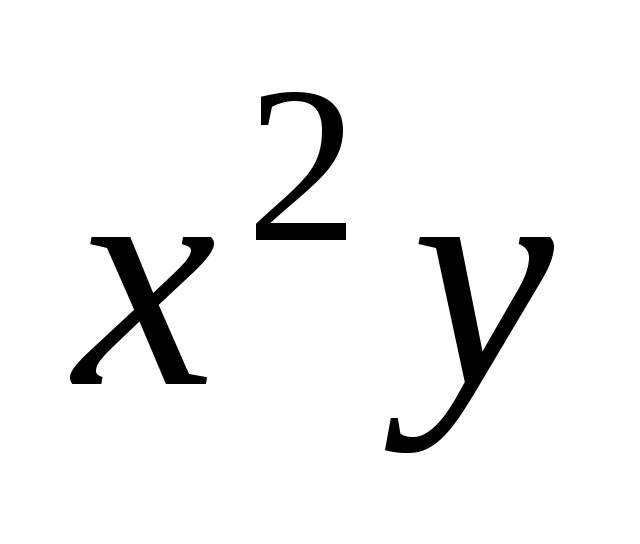
1
0.78
0.608
0.475
0.370
2.50
1.950
1.521
1
1.56
2.434
3.796
5.922
1.20
1.872
2.920
1
2.34
5.476
12.813
29.982
1.12
2.621
6.133
1
3.12
9.734
30.371
94.759
2.25
7.020
21.902
1
3.81
14.516
55.306
210.717
4.28
16.307
62.129
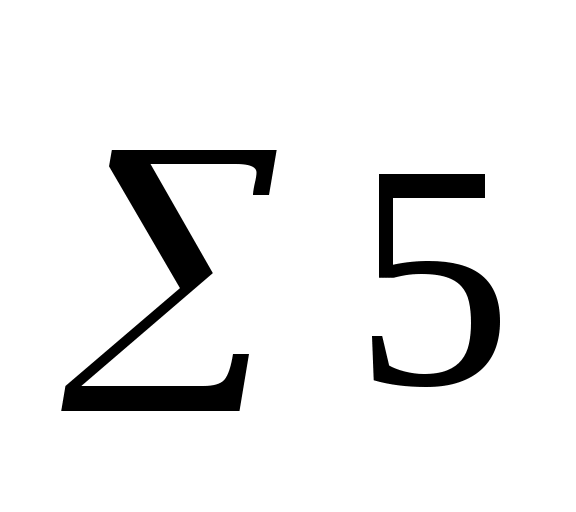
11.61
32.768
102.761
341.750
11.35
29.770
94.605
а) Линейная модель
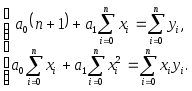
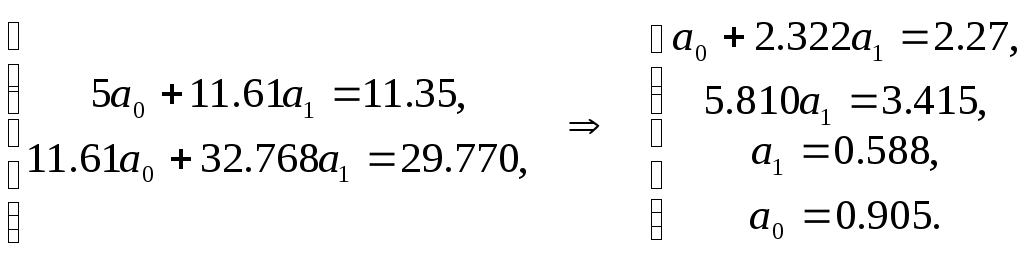
Таким образом, линейная модель имеет вид
б) Квадратичная модель
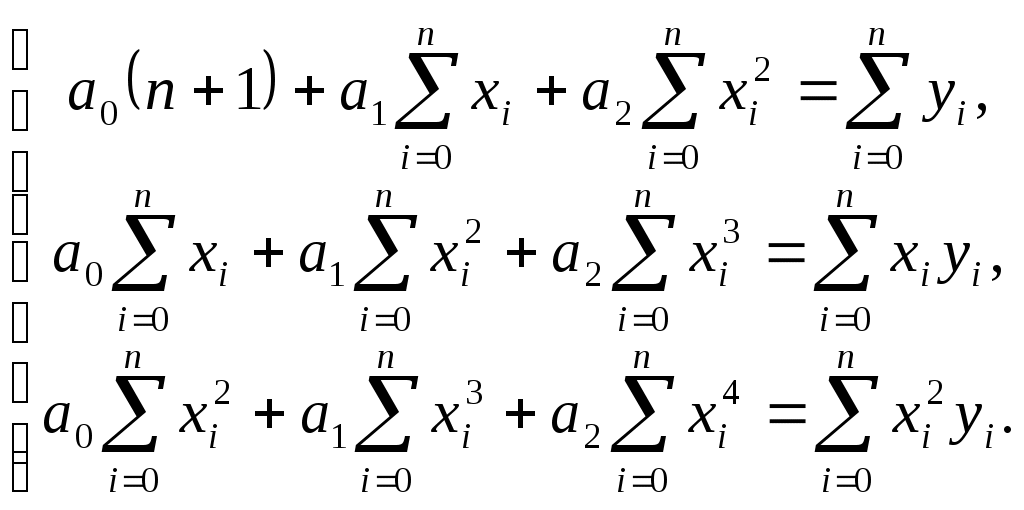
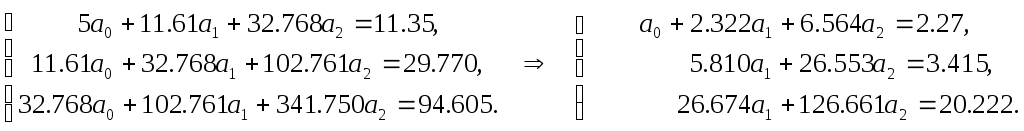
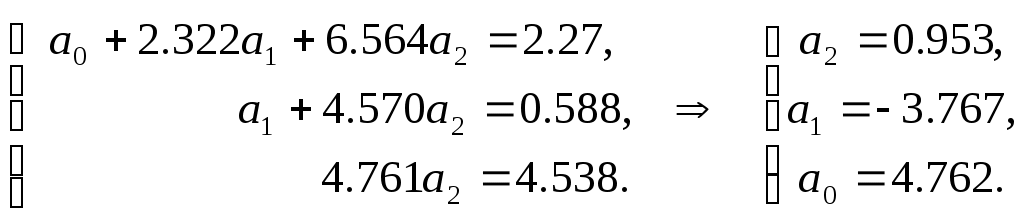
Отсюда
-


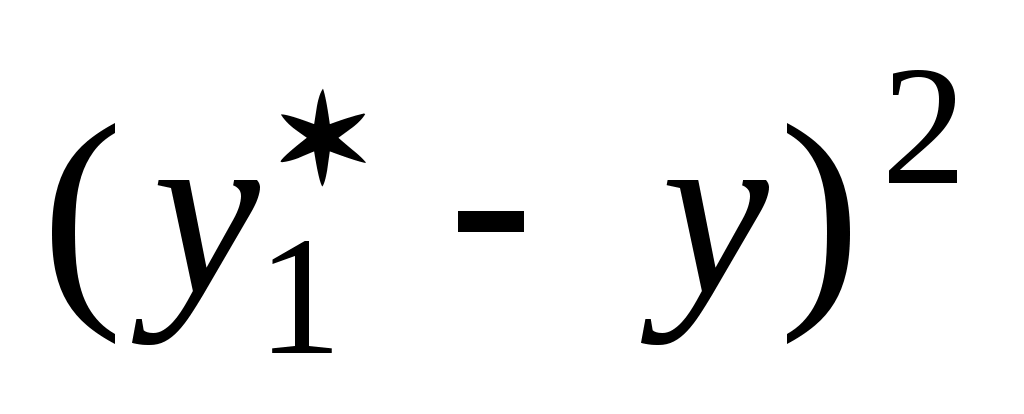

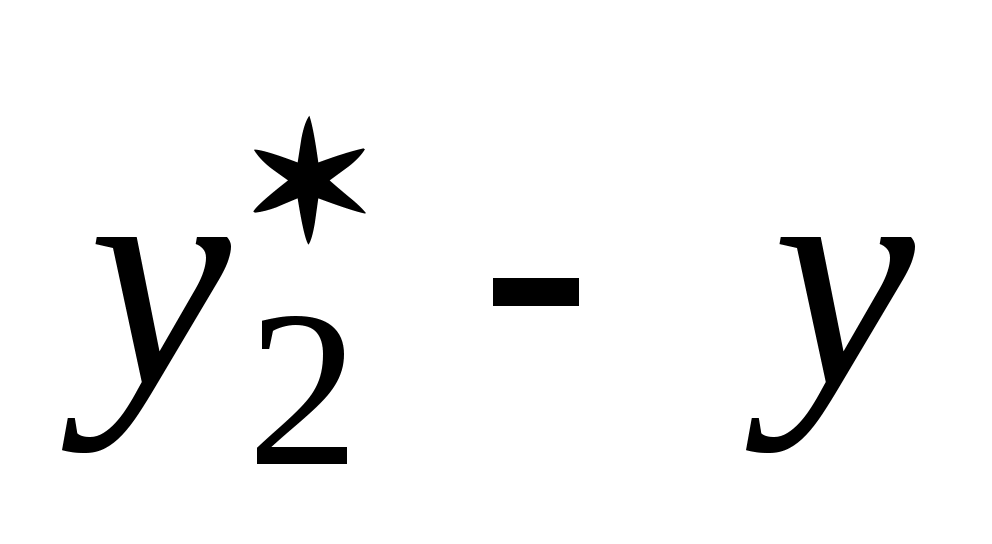
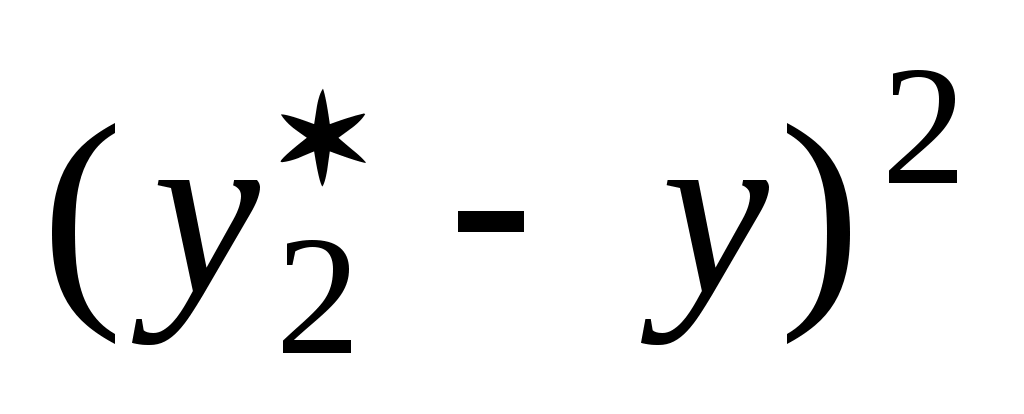
0.78
2.50
1.364
-1.136
1.290
2.404
-0.096
0.009
1.56
1.20
1.822
0.622
0.387
1.204
0.004
0.000
2.34
1.12
2.281
1.161
1.350
1.165
0.045
0.002
3.12
2.25
2.740
0.490
0.240
2.286
0.036
0.001
3.81
4.28
3.145
1.135
1.290
4.244
-0.036
0.001
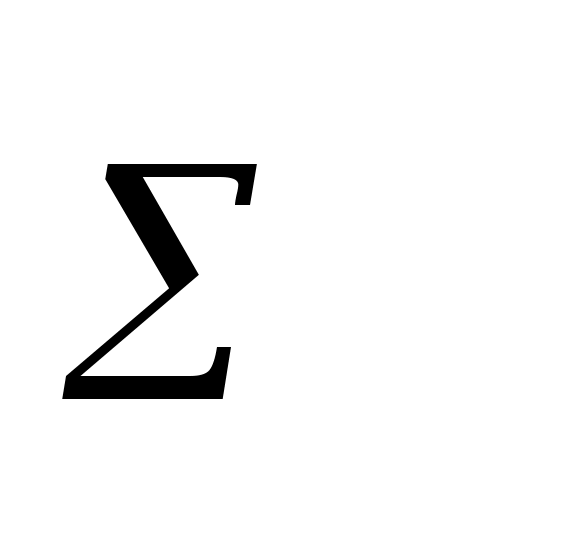
4.557
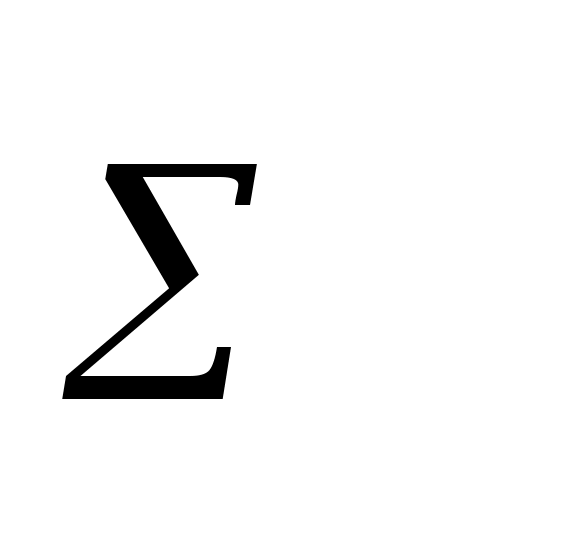
0.013
Таким образом,
3.2. Лабораторная работа № 4. Аппроксимация функции по методу наименьших квадратов
Очень часто при анализе эмпирических данных необходимо найти явную функциональную зависимость между двумя величинами
Итак, если
В подразделе 3.1 описан пример «ручного» вычисления коэффициентов линейной и квадратичной модели по методу наименьших квадратов. Решим аналогичную задачу средствами пакета Mathcad различными способами. Сформируем вначале вектора исходных данных.
В алгебре матриц в среде Mathcad доступны несколько очень удобных встроенных функций, например, submatrix, stack и augment. Функция
и со столбца с номером
Введем с клавиатуры
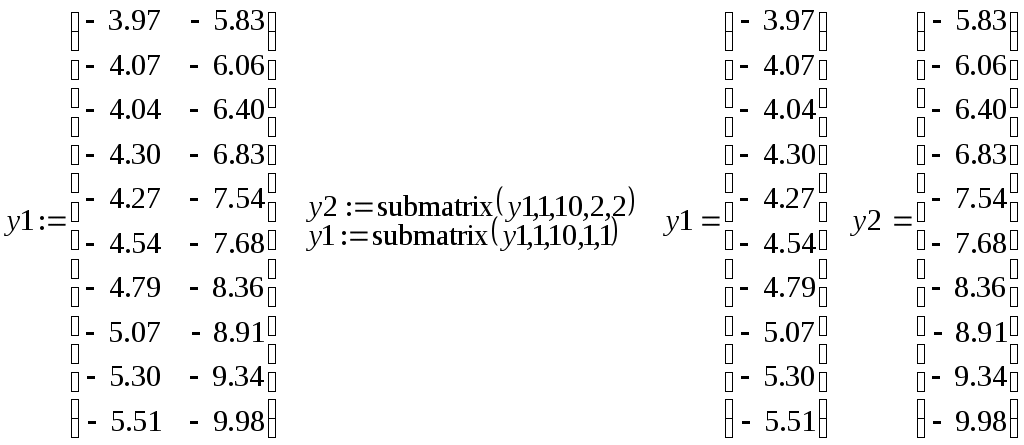

Функции