Файл: 3. Метод наименьших квадратов и специальные интерполяционные многочлены.doc
Добавлен: 30.11.2023
Просмотров: 86
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Метод наименьших квадратов и специальные интерполяционные многочлены
3.1. Постановка задачи и вывод формул метода наименьших квадратов
3.2. Лабораторная работа № 4. Аппроксимация функции по методу наименьших квадратов
3.3. Глобальная полиномиальная интерполяция
3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
3.3. Глобальная полиномиальная интерполяция
Пусть функция
Теорема 3.1. Пусть функция
Однако существуют очень веские причины, по которым глобальная интерполяция многочленами высокой степени в вычислительной практике не используется. Обычный подход увеличения точности интерполяции - увеличение числа узлов. Однако не существует единой для всех непрерывных на отрезке
Классический пример - функция Рунге
. Если использовать глобальную аппроксимацию на
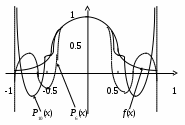 лева). Таким образом, равномерное распределение узлов оказалось неудачным. Итак, не существует единой для всякой функции
лева). Таким образом, равномерное распределение узлов оказалось неудачным. Итак, не существует единой для всякой функции Теорема 3.2. Какова бы ни была стратегия выбора узлов интерполяции,
найдется непрерывная на отрезке
Однако если функция гладкая (непрерывно дифференцируемая), то такая стратегия существует.
Теорема 3.3. Пусть в качестве узлов интерполяции на отрезке
Практическая реализация стратегии выбора узлов интерполяции возможна и оправдана в довольно редких случаях и просто невозможна тогда, когда приходится иметь дело с заданной таблицей значений функции.
3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
Помимо погрешности от приближенной замены
Пусть известно, что верхняя граница погрешности
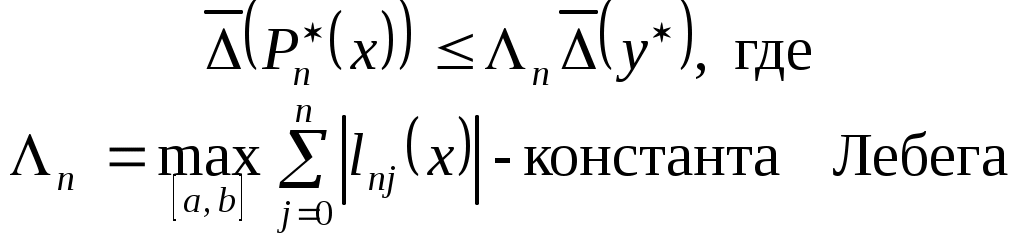 . (3.4.1)
. (3.4.1)В задаче интерполирования константа Лебега играет роль абсолютного числа обусловленности, то есть в самом неблагоприятном случае погрешность входных данных при интерполяции может возрасти в
расположения узлов интерполяции. Например, если в качестве узлов интерполяции взяты нули многочленов Чебышева, то
Если же узлы равноотстоящие, то
3.5. Многочлены Чебышева
Система функций
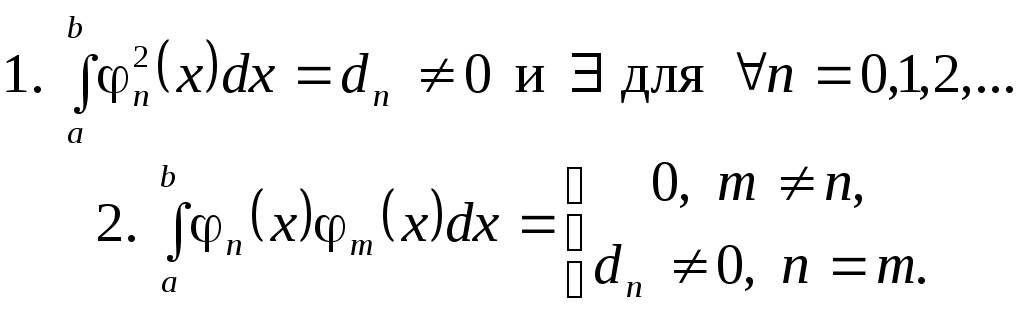 (3.5.1)
(3.5.1)Система функций
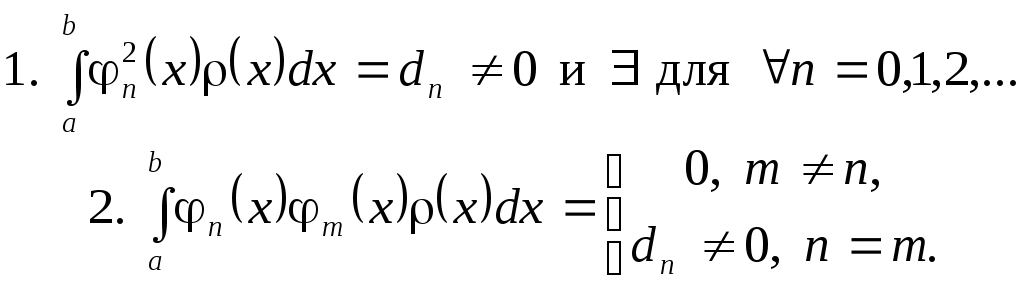 (3.5.2)
(3.5.2)Функция
В качестве примера системы функций, ортогональной с весом, приведем многочлены Чебышева, которые известны еще и тем, что являются полиномами, наименее уклоняющимися от нуля. Эти многочлены определяют разными способами. Например: