Файл: Реферат применение формулы Байеса в профессии и в экономике студент группы 38. 03. 02.rtf
Добавлен: 30.11.2023
Просмотров: 136
Скачиваний: 3
СОДЕРЖАНИЕ
Основные понятия и определения
Введение в байесовские сети доверия.
Моделирование в условиях неопределенности
Экспертные системы и формальная логика
Особенности вывода суждений в условиях неопределенности
Использование Байесовых сетей.
Вероятности прогнозируемых значений отдельных переменных
Пример построения простейшей байесовской сети доверия.
Байесовские сети доверия как одно из направлений современных экспертных систем.
Представление знаний с использованием байесовской сети доверия и условная независимость событий.
Замечание о субъективных вероятностях и ожидания.
Синтез сети на основе априорной информации.
Пример использования Байесовых сетей
Космические и военные применения
Компьютеры и системное программное обеспечение
AUAI — Ассоциация анализа неопределенности в искусственном интеллекте
Расчет в байесовской сети.
Следует отметить, что следствием байесовской теоремы является то, что она поддерживает оценку графа в обоих направлениях. Процесс рассуждения в ЭС сопровождается распространением по сети вновь поступивших свидетельств.
Введение в байесовские сети доверия новых данных приводит к возникновению переходного процесса распространения по байесовской сети доверия вновь поступившего свидетельства. После завершения переходного процесса каждому высказыванию, ассоциированному с вершинами графа, приписывается апостериорная вероятность, которая определяет степень доверия к этому высказыванию ( believe – доверять(англ.) ):
где D – объединения всех поступивших в систему данных;
Vji – композиционные высказывания, составленные из элементарных, то есть множество значений Xi составляют Vji ;
Xi – пропозиционные переменные (то есть переменные, значениями которых являются высказывания), определяющие состояние вершин БСД.
При этом процесс распространения вероятностей в БСД основывается на механизме пересчёта, в основе функционирования которого лежит следующая последовательность действий:
С каждой вершиной сети ассоциирован вычислительный процесс (процессор), который получает сообщения от соседних (связанных с ним дугами) процессоров.
Этот процессор осуществляет пересчёт апостериорных вероятностей Bel(Vji) для всех возможных значений Vji данной переменной Xi и посылает соседим вершинам ответные сообщения.
Деятельность процессора инициируется нарушением условий согласованности с состояниями соседних процессоров и продолжается до восстановления этих условий.
В некоторых системах, реализующих байесовские сети доверия используется метод noisy or gate, позволяющий существенно упростить вычислительный процесс. Суть его заключается в том, что в ряде примеров вершина «y» может быть условно независима от целого ряда вершин «xr» , где r = 1,2,..., n. Для того, чтобы сократить оценку 2n вероятностей, которые необходимы при использовании таблиц условных вероятностей
, и используется данный метод. Согласно ему вероятность «y» в зависимости от n вершин «xr» оценивается как
что позволяет оценить только p(y | x 1), p(y | x 2) ... p(y | x n), и на их основании определить оценку p( y | x1 x2 ... xn).
Байесовские сети доверия как одно из направлений современных экспертных систем.
Выбор байесовских сетей доверия в качестве ЭС по сравнению с другими направлениями их построения обусловлен рядом причин.
1.Логический вывод в байесовских сетях доверия является трактуемым с вычислительной точки зрения, так как теория, лежащая в его основе, имеет аксиоматическое обоснование, отработанное в течение последних десятилетий. В то время, как системы, основанные на теории нечётких множеств, на теории функций доверия, теории Демпстера - Шефера не имеет строгого математического обоснования и в большинстве случаев используют эвристические процедуры ( ЭС типа MYCIN, EMYCIN и т.д.).
2.Показано, что психологически проще выполнять субъективное вероятностное оценивание причинно-следственных связей.
3.Метод noisy or gate обеспечивает эффективное вычисление условных вероятностей.
4.Несмотря на то, что теорию вероятности зачастую критикуют с точки зрения её использования в «знаниях», она не нарушает общих представлений о «замкнутом мире» объектов.
Представление знаний с использованием байесовской сети доверия и условная независимость событий.
Рассмотрим фрагмент представления медицинской БЗ, в которой можно выделить
заболевания, симптомы их проявления, а также факторы риска, влияющие на возникновение
заболеваний. Пусть некоторая упрощённая модель качественного описания БЗ имеет вид,
приведенный на рис.2. Эта модель соответствует следующему набору медицинских знаний:
Одышка [o] может быть вследствие туберкулёза [t], рака лёгких [r] или бронхита [b], а также
вследствие ни одного из перечисленных заболеваний или более, чем одного.
Визит в Азию [a] повышает шансы туберкулёза [t].
Курение [k] – фактор риска, как для рака [r], так и бронхита [b].
Результаты рентгена, определяя затемнённость в лёгких не позволяют различить рак [r] и
туберкулёз [t], так же как не определяет факт наличия или отсутствия одышки [o].
Последний факт представляется в графе промежуточной переменной (событием) [tr]. Эта
переменная соответствует логической функции «или» для двух родителей ([t] и [r]) и она
означает наличие либо одной, либо двух болезней или их отсутствие.
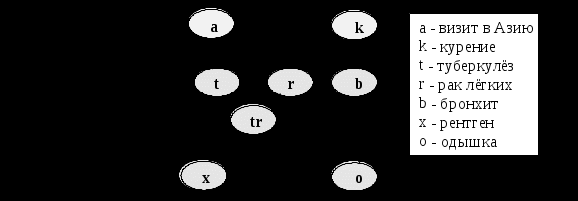
Рис.2. Представление фрагмента модели медицинской БЗ в виде БСД.
Важное понятие байесовской сети доверия – это условная независимость случайных переменных, соответствующих вершинам графа. Две переменные A и B являются условно независимыми при данной третьей вершине C, если при известном значении C, значение B не увеличивает информативность о значениях A, то есть
p ( A | B, C ) = p ( A | C ) .
Если имеется факт, что пациент курит, то мы устанавливаем наши доверия относительно рака и бронхита. Однако наши доверия относительно туберкулёза не изменяются. То есть [t] условно не зависит, от [k] при данном пустом множестве переменных
p ( t | k ) = 0
Поступления положительного результата рентгена пациента повышают наши доверия относительно туберкулёза и рака, но не относительно бронхита. То есть [b] – условно не зависит от [x] при данном k
p ( b | x, k ) = p ( b | k )
Однако, если бы знали также, что у пациента учащённое дыхание [o], то рентгеновские результаты также имели бы воздействие на наше доверие относительно бронхита. То есть [b] условно зависит от [x] при данных o и k. Таким образом, логический вывод в БСД означает вычисление условных вероятностей для одних переменных при наличии информации (свидетельств) о других. При этом для распространения вероятностей используется теорема Байеса.
Замечание о субъективных вероятностях и ожидания.
Исчисление вероятностей формально не требует, чтобы использованные вероятности базировались на теоретических выводах или представляли собой пределы эмпирических частот. Числовые значения в байесовых сетях могут быть также и субъективными, личностными, оценками ожиданий экспертов по поводу возможности осуществления событий. У разных лиц степень ожидания (надежды или боязни — по Лапласу) события может быть разной, это зависит от индивидуального объема априорной информации и индивидуального опыта.
Предложен оригинальный способ количественной оценки субъективных ожиданий. Эксперту, чьи ожидания измеряются, предлагается сделать выбор в игре с четко статистически определенной вероятностью альтернативы—поставить некоторую сумму на ожидаемое событие, либо сделать такую же ставку на событие с теоретически известной вероятностью (например, извлечение шара определенного цвета из урны с известным содержанием шаров двух цветов). Смена выбора происходит при выравнивании степени ожидания эксперта и теоретической вероятности. Теперь об ожидании эксперта можно (с небольшой натяжкой) говорить как о вероятности, коль скоро оно численно равно теоретической вероятности некоторого другого статистического события.
Использование субъективных ожиданий в байесовых сетях является единственной альтернативой на практике, если необходим учет мнения экспертов (например, врачей или социологов) о возможности наступления события, к которому неприменимо понятие повторяемости, а также невозможно его описание в терминах совокупности элементарных событий.
Синтез сети на основе априорной информации.
Как уже отмечалось, вероятности значений переменных могут быть как физическими (основанными на данных), так и байесовыми (субъективными, основанными на индивидуальном опыте). В минимальном варианте полезная байесова сеть может быть построена с использованием только априорной информации (экспертных ожиданий).Для синтеза сети необходимо выполнить следующие действия:
-
сформулировать проблему в терминах вероятностей значений целевых переменных; -
выбрать понятийное пространство задачи, определить переменные, -
имеющие отношение к целевым переменным, описать возможные -
значения этих переменных; -
выбрать на основе опыта и имеющейся информации априорные вероятности значений -
переменных; -
описать отношения «причина-следствие» (как косвенные, так и прямые) в виде -
ориентированных ребер графа, разместив в узлах переменные задачи; -
для каждого узла графа, имеющего входные ребра указать оценки -
вероятностей различных значений переменной этого узла в зависимости от комбинации -
значений переменных-предков на графе.
Эта процедура аналогична действиям инженера по знаниям при построении экспертной
системы в некоторой предметной области. Отношения зависимости, априорные и условные
вероятности соответствуют фактам и правилам в базе знаний ЭС.
Построенная априорная байесова сеть формально готова к использованию. Вероятностные
вычисления в ней проводятся с использованием уже описанной процедуры маргинализации
полной вероятности.
Дальнейшее улучшение качества прогнозирования может быть достигнуто путем обучения байесовой сети на имеющихся экспериментальных данных. Обучение традиционно разделяется на две составляющие — выбор эффективной топологии сети, включая, возможно, добавление новых узлов, соответствующих скрытым переменным, и настройка параметров условных распределений для значений переменных в узлах.
Пример использования Байесовых сетей
Естественной областью использования байесовых сетей являются экспертные системы,
которые нуждаются в средствах оперирования с вероятностями.
Медицина
Система PathFinder (Heckerman, 1990) разработана для диагностики заболеваний лимфатических узлов. PathFinder включает 60 различных вариантов диагноза и 130 переменных, значения которых могут наблюдаться при изучении клинических случаев. Система смогла приблизиться к уровню экспертов, и ее версия PathFinder-4 получила коммерческое распространение.
Множество других разработок (Child, MUNIN, Painulim, SWAN и др.) успешно применяются в различных медицинских приложениях .
Космические и военные применения
Система поддержки принятия решений Vista (Eric Horvitz) применяется в Центре управления полетами NASA (NASA Mission Control Center) в Хьюстоне. Система анализирует телеметрические данные и в реальном времени идентифицирует, какую информацию нужно выделить на диагностических дисплеях.
В исследовательской лаборатории МО Австралии системы, основанные на байесовых сетях, рассматриваются, как перспективные в тактических задачах исследования операций. Модель включает в себя различные тактические сценарии поведения сторон, данные о передвижении судов, данные разведнаблюдений и другие переменные. Последовательное поступление информации о действиях противников позволяет синхронно прогнозировать вероятности различных действий в течение конфликта.